Содержание
- 2. Цель работы: освоение инструментария Поиск решения для решения оптимизационных задач в MS Excel.
- 3. Пример 1: Задача определения оптимального ассортимента продукции Предприятие изготавливает четыре вида продукции – A, B, C
- 5. Прибыль от реализации единицы продукции равны: 8 д. е. – для A, 10 д. е. –
- 6. Решение. Составим математическую модель для решения поставленной задачи. Обозначим переменные: x1 – объем произведенной продукции вида
- 8. Прибыль от реализации продукции составит: Cреди всех неотрицательных решений системы линейных неравенств требуется найти такое, при
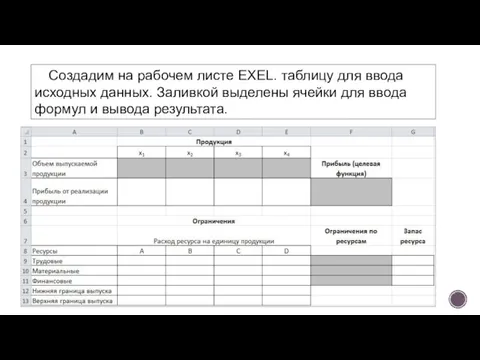
- 9. Создадим на рабочем листе EXEL. таблицу для ввода исходных данных. Заливкой выделены ячейки для ввода формул
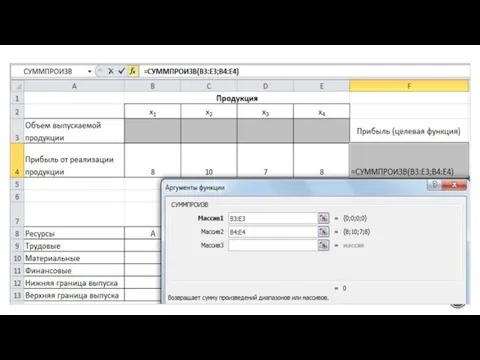
- 10. Заполним таблицу. Блок ячеек В3:Е3 содержит оптимальное решение, значение этих ячеек будет получено в результате решения
- 12. В ячейки F9:F11 введены формулы для расчета ограничений по ресурсам. Ниже представлена таблица с исходными данными,
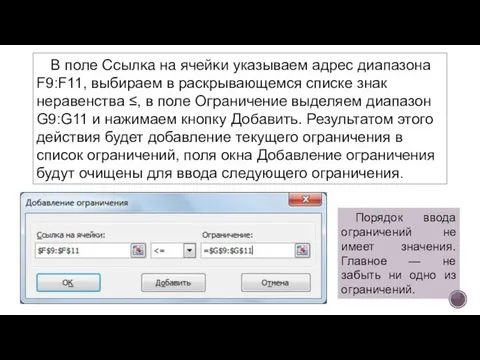
- 13. Остановимся подробно на добавлении ограничений в область В соответствии с ограничениями. Все ограничения указаны в системе.
- 14. В поле Ссылка на ячейки указываем адрес диапазона F9:F11, выбираем в раскрывающемся списке знак неравенства ≤,
- 15. Ограничения ?2 ≥ 0 и ?4 ≥ 0 можно не добавлять, т.к. в окне Параметры поиска
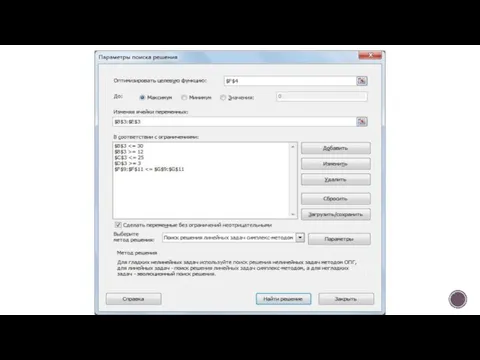
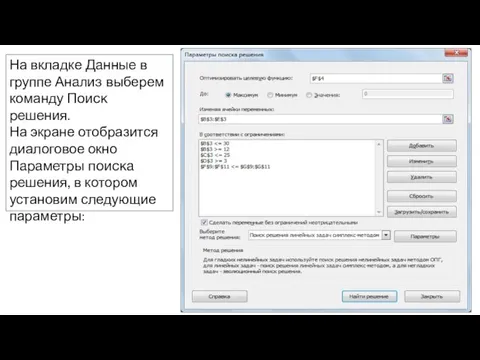
- 17. На вкладке Данные в группе Анализ выберем команду Поиск решения. На экране отобразится диалоговое окно Параметры
- 18. в поле Оптимизировать целевую функцию указываем адрес ячейки со значением целевой функции – F4; выбираем нахождение
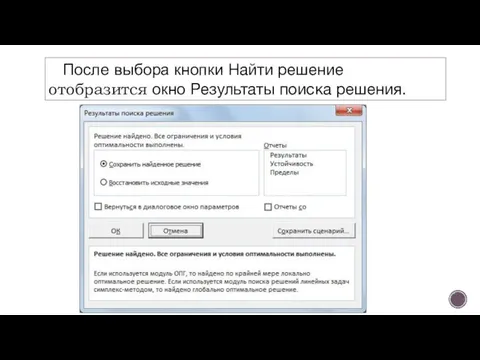
- 19. После выбора кнопки Найти решение отобразится окно Результаты поиска решения.
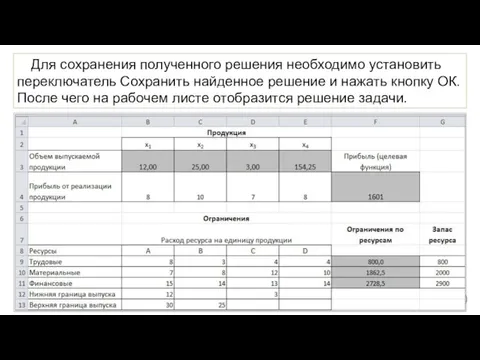
- 20. Для сохранения полученного решения необходимо установить переключатель Сохранить найденное решение и нажать кнопку ОК. После чего
- 21. Таким образом, максимальная прибыль при реализации продукции будет получена в размере 1601 д. е. при следующем
- 22. Кроме вставки оптимальных значений в изменяемые ячейки, Поиск решения позволяет представлять результаты в виде трех отчетов:
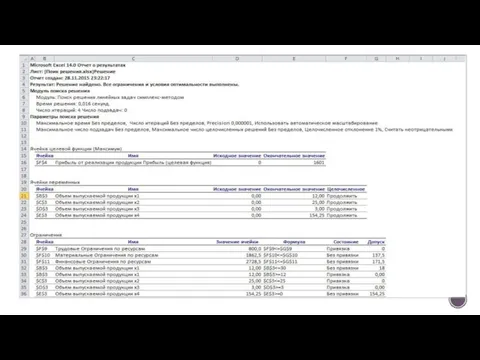
- 23. Отчет по результатам содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления
- 24. По значениям столбца Допуск можно сделать вывод о недоиспользованных ресурсах. В рассматриваемой задаче трудовые ресурсы были
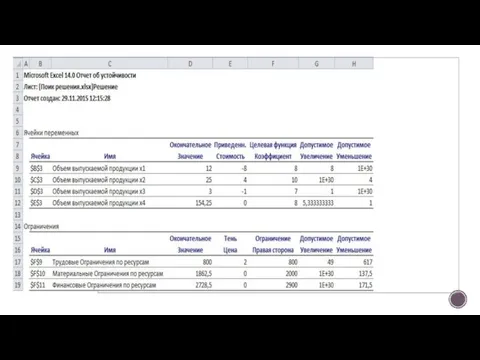
- 26. Отчет по устойчивости содержит два блока: Ячейки переменных и Ограничения. Первый блок содержит информацию по допустимому
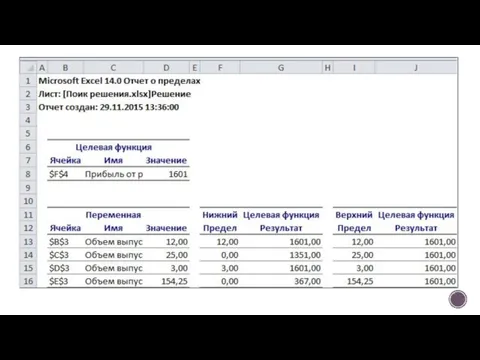
- 28. Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены
- 31. Скачать презентацию





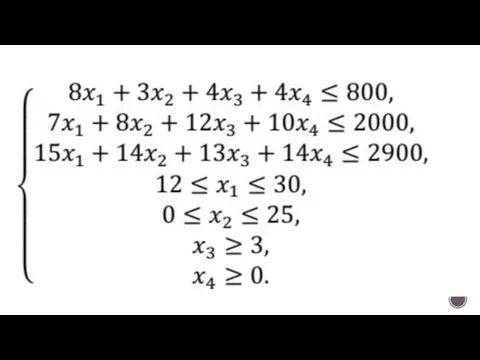












 Ресторан Золотой дракон
Ресторан Золотой дракон Конфлікти в закладі дошкільної освіти
Конфлікти в закладі дошкільної освіти Игра Пирамида
Игра Пирамида Как человек открывал Землю
Как человек открывал Землю Занимательные клеточки
Занимательные клеточки Компьютерные вирусы
Компьютерные вирусы FN1_LessonOne
FN1_LessonOne Цилиндр и конус
Цилиндр и конус Основы работы профБюро факультета
Основы работы профБюро факультета Педагогический советГОУ СОШ № 547 протокол № 1 от 30.08.2010 г.
Педагогический советГОУ СОШ № 547 протокол № 1 от 30.08.2010 г. Сборник артикуляционных упражнений
Сборник артикуляционных упражнений Темперамент. Для учащихся 5 класса
Темперамент. Для учащихся 5 класса Инжиниринговый центр Краснодарского края
Инжиниринговый центр Краснодарского края Древний Китай
Древний Китай Гимнастика
Гимнастика Методология проекта. Культура Японии
Методология проекта. Культура Японии Окказионализмы в детском словотворчестве
Окказионализмы в детском словотворчестве История развития пожарного дела в России
История развития пожарного дела в России Звук К
Звук К RoomTour show. Экскурсия по домам медийных личностей
RoomTour show. Экскурсия по домам медийных личностей Внеплановая Чёрная Пятница теперь в М.Видео
Внеплановая Чёрная Пятница теперь в М.Видео Формирование ключевых компетенций средствами межпредметной интеграции и использованием регионального компонента
Формирование ключевых компетенций средствами межпредметной интеграции и использованием регионального компонента Исследование уровня интернет-зависимости уучащихся
Исследование уровня интернет-зависимости уучащихся Этика, культура делового общения
Этика, культура делового общения Сон Иосифа
Сон Иосифа Что такое техника?
Что такое техника? Перспективы развития информационных технологий в библиотечной сфере Хабаровского края
Перспективы развития информационных технологий в библиотечной сфере Хабаровского края Наркотизм и национальная безопасность. Тест
Наркотизм и национальная безопасность. Тест