Оптимизация задач в менеджменте

Моделювання для прийняття рішень
Вивчені нами статистичні методи прийняття рішень, в основному, дозволяють відповісти на питання “Що є чи що буде?”.
Якщо б ми змогли змоделювати весь чи частину процесів у нашому бізнесі, то крім цього питання ми б могли дати відповідь на питання “Що буде, якщо ... ?”, тобто ми б могли прораховувати різні варіанти прийняття рішень та дивитись на можливі наслідки.

Моделювання для прийняття рішень: приклад
Компанія розглядає можливість продажу нового продукту і потребує оцінити оптимальну кількість замовлення цього товару у виробника. Компанія планує продавати товар за $30. Виробник пропонує різну ціну товару в залежності від замовлення. Якщо замовлення менше 1000 шт., то ціна рівна $24, між 1000 та 2000 шт. ціна рівна $23, між 2000 та 3000 шт. ціна $22.25, між 3000 та 4000 шт. ціна $21.75 і при замовленні більше 4000 шт. ціна рівна $21.30. Тобто, замовивши, наприклад, 2500 шт. товару ціна замовлення для компанії складе $22.25*2500=$55 625. Також, весь непроданий товар компанія може повернути за ціною $10 за шт. Компанія не впевнена в попиті на товар, тому не знає скільки замовити товару. Допоможіть!
Також, припустимо, що базуючись на попередньому досвіді компанія очікує такий розподіл ймовірного попиту на новий товар:

Моделювання для прийняття рішень: приклад
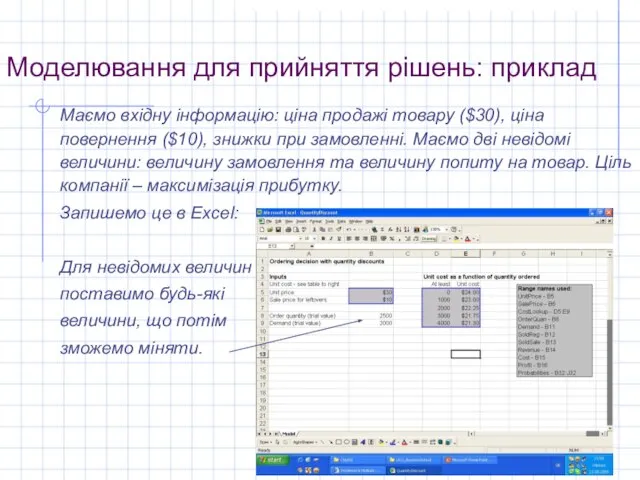
Маємо вхідну інформацію: ціна продажі товару ($30), ціна повернення ($10), знижки при замовленні. Маємо дві невідомі величини: величину замовлення та величину попиту на товар. Ціль компанії – максимізація прибутку.
Запишемо це в Excel:
Для невідомих величин
поставимо будь-які
величини, що потім
зможемо міняти.

Моделювання для прийняття рішень: приклад
Далі запишемо модель для визначення прибутку. Для цього визначимо кількість товару проданого за звичайною ціною як менше з величини замовлення та попиту (=MIN(OrderQuan;Demand)).
Якщо замовлено більше ніж продано, то ця величина визначається наступним чином (=IF(OrderQuan>Demand;OrderQuan-Demand;0)).
Далі, визначаємо дохід як к-кість проданого товару на його звичайну ціну плюс к-кість непроданого товару на ціну повернення (=SoldReg*UnitPrice+SoldSale*SalePrice).
Витрати – це ціна замовлення, що залежить від величини замовлення, оскільки діє система знижок. Щоб це записати в Excel використаємо функцію VLOOKUP, а саме (=VLOOKUP(OrderQuan;CostLookup;2)*OrderQuan).
Нарешті, прибуток = дохід – витрати (=Revenue-Cost).

Моделювання для прийняття рішень: приклад
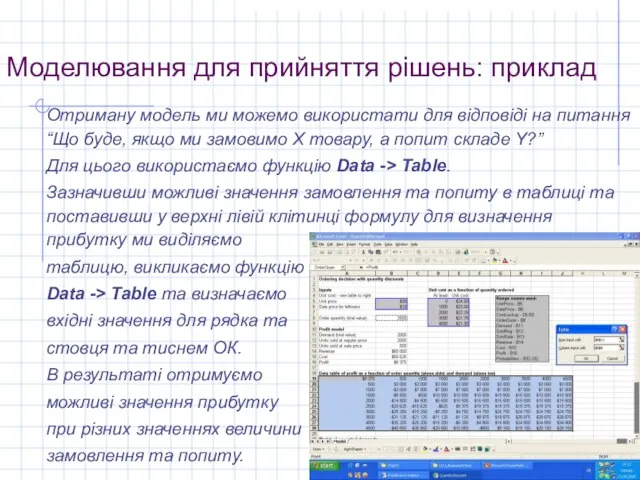
Отриману модель ми можемо використати для відповіді на питання “Що буде, якщо ми замовимо Х товару, а попит складе Y?”
Для цього використаємо функцію Data -> Table.
Зазначивши можливі значення замовлення та попиту в таблиці та поставивши у верхні лівій клітинці формулу для визначення прибутку ми виділяємо
таблицю, викликаємо функцію
Data -> Table та визначаємо
вхідні значення для рядка та
стовця та тиснем ОК.
В результаті отримуємо
можливі значення прибутку
при різних значеннях величини
замовлення та попиту.

Моделювання для прийняття рішень: приклад
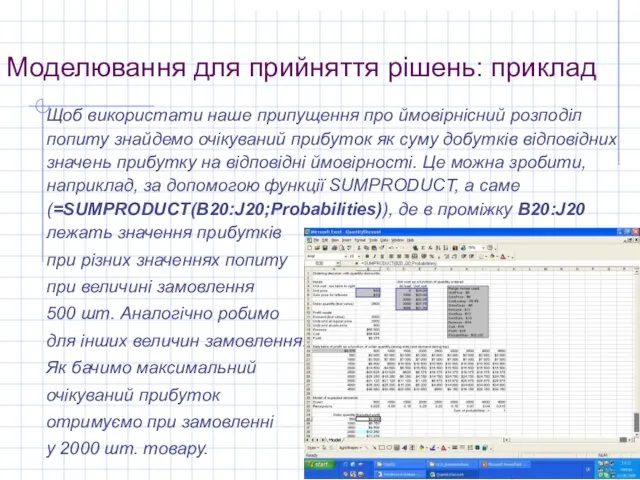
Щоб використати наше припущення про ймовірнісний розподіл попиту знайдемо очікуваний прибуток як суму добутків відповідних значень прибутку на відповідні ймовірності. Це можна зробити, наприклад, за допомогою функції SUMPRODUCT, а саме (=SUMPRODUCT(B20:J20;Probabilities)), де в проміжку B20:J20 лежать значення прибутків
при різних значеннях попиту
при величині замовлення
500 шт. Аналогічно робимо
для інших величин замовлення.
Як бачимо максимальний
очікуваний прибуток
отримуємо при замовленні
у 2000 шт. товару.

Моделювання для прийняття рішень:
лінійне програмування
Зазвичай цілі будь-якого бізнесу зазвичай формулюються в термінах максимізації чи мінімізації певних величин, як от максимізація прибутку.
Лінійне програмування (ЛП) – це розв’язування задач опитмізації.
Класична задача лінійного програмування – це оптимізувати певний (лінійний) процес при заданих обмеженнях.
ЛП складає невід’ємну частину фактично будь-якої системи прийняття рішень і вирішує задачі фактично з будь-якому аспекті ведення бізнесу.
Наша задача – зрозуміти суть ЛП, розглянути ряд застосувань ЛП для різних аспектів ведення бізнесу та навчитись його застосовувати використовуючи Excel та його надбудови.

ЛП: приклад вибору оптимального
набору товарів (product mix problem)
Для цього типу задач проблема полягає в пошуку оптимального набору товарів виробництва для максимізації прибутку.
Компанія Monet випускає чотири типи фоторамок (1, 2, 3 та 4) що відрізняються у розмірі, формі та матеріалах. Кожен тип рамки вимагає певних кваліфікованих людських ресурсів, металу та шкла.
Наразі на ринку максимально можна отримати до 4000 годин людських ресурсів, 6000 одиниць металу та 10000 одиниць шкла за ціною, відповідно, $8/год., $0.5 та $0.75. Також, ринкові умови є такі, що неможлтво продати білье 1000 рамок 1, 2000 рамок 2, 500 рамок 3 та 1000 рамок 4. Який оптимальний набір рамок для максимізації прибутку?

ЛП: приклад вибору оптимального
набору товарів (product mix problem)
Спочатку знайдемо прибуток від однієї рамки кожного типу. Для рамки 1 маємо: $28.50-(2*$8+4*$0.5+6*$0.75)=$6. Для рамок 2, 3 та 4 маємо, відповідно, $2, $4 та $3. Отже, якщо через X1, X2, X3 та X4 позначимо кількість рамок кожного типу, то наша задача така:
max 6X1+2X2+4X3+3X4 (наша ціль)
2X1+X2+3X3+2X4 ≤ 4000 (обмеження робочої сили)
4X1+2X2+X3+2X4 ≤ 6000 (обмеження пропозиції металу)
6X1+2X2+X3+2X4 ≤ 10000 (обмеження пропозиції шкла)
X1 ≤ 1000 (обмеження попиту)
X2 ≤ 2000 (обмеження попиту)
X3 ≤ 500 (обмеження попиту)
X4 ≤ 1000 (обмеження попиту)
X1, X2, X3, X4 ≥ 0 (кількості є позитивними числами)

ЛП: приклад вибору оптимального
набору товарів (product mix problem)
Для запису та розв’язання задачі в Excel нам потрібно розділити всі змінні в залежності від їх типу:
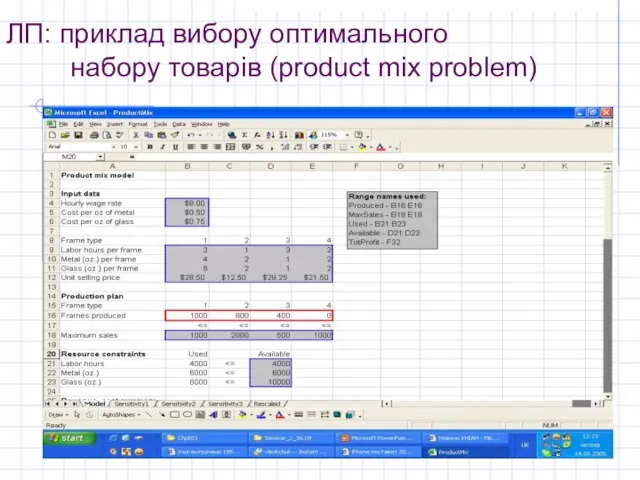
1. Вхідні дані (Inputs): всі числові дані з умови задачі;
2. Змінні (Changing cells): кількості рамок кожного типу;
3. Цілова змінна (Target, objective cell): прибуток, як функція від вхідних даних та змінних;
Також важливим елементом запису задачі в Excel є формулювання обмежень.

ЛП: приклад вибору оптимального
набору товарів (product mix problem)

ЛП: приклад вибору оптимального
набору товарів (product mix problem)
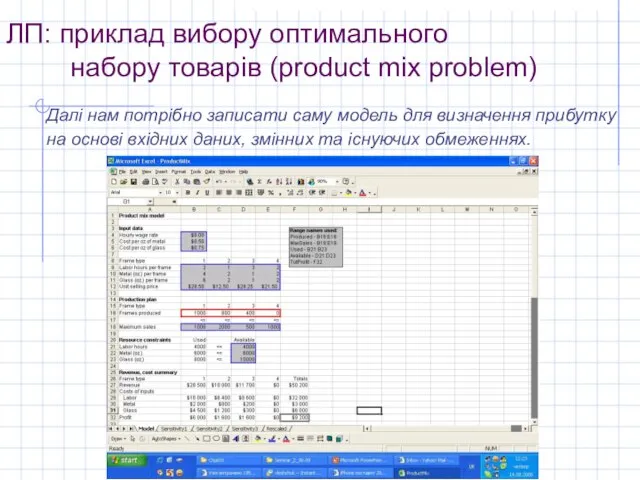
Далі нам потрібно записати саму модель для визначення прибутку на основі вхідних даних, змінних та існуючих обмеженнях.

ЛП: приклад вибору оптимального
набору товарів (product mix problem)
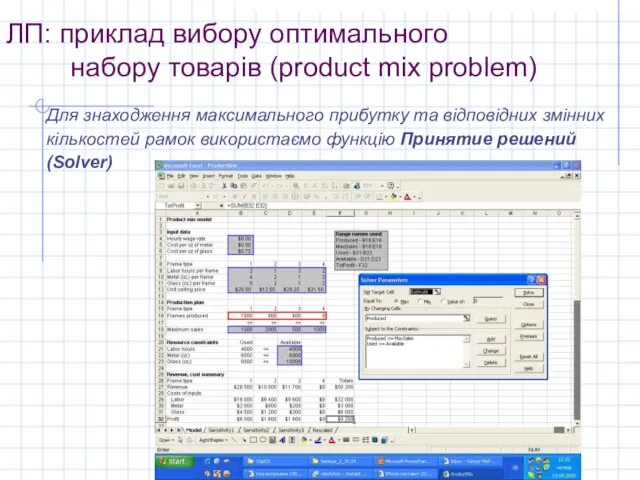
Для знаходження максимального прибутку та відповідних змінних кількостей рамок використаємо функцію Принятие решений (Solver)

ЛП: приклад вибору оптимального
набору товарів (product mix problem)
Знаходження оптимального набору товарів та відповідного прибутку не завершує, а лише починає аналіз. Далі можна робити всеможливі аналізи чутливості ставлячи різні варіанти змін у вхідні дані. Наприклад, як зміниться оптимальний набір товарів, якщо збільшити ціну рамки 4 з $21.50 до $26.50. Зрозуміло, що прибуток збільшиться, але на скільки? Зробивши відповідну заміну в вхідних даних та викликавши функцію Solver знов отримуємо, що максимальний прибуток зросте з $9200 до $14000.
Дякуючи додатку Solver Table ми можемо автоматизувати зміну вхідних даних. Виклакавши функцію Data -> Solver Table ми можемо автоматизувати зміну одного або двох вхідних параметрів одночасно.
Припустимо, ми хочемо подивитись як змінюється максимальний прибуток та відповідний набір товарів при зміні наявної робочої сили з 2500 до 5000 годин (з кроком 250 год.). Як це зробити?

ЛП: мережні моделі
Багато оптимізаційних задач можуть бути зображеня у вигляді мереж (графів). У бізнесі такі задачі зазвичай трапляються у логістиці, як от транспортна задача чи оптимізація виконання проектів.
Простим прикладом транспортної задачі є задача компанії, що має декілька центрів виробництва та декілька центрів споживання товару. Кожен центр характеризується певним максимальним обсягом виробництва чи споживання товару. Задача компанії полягає в мінімізації коштів на транспортування товару з центрів виробництва в центри споживання товару.

ЛП: мережні моделі –
оптимізація виконання проектів
Мережеві моделі можна використати для оптимізації таймінгу комплексних проектів, що складаються з багатьох етапів. Якщо відомий точний час для виконання кожного етапу, то ЛП дозволяє визначити час необхідний для виконання проекту. Якщо ж невідомий час виконання певних етапів, то можна оцінити ймовірність виконання проекту за певний час.
Прикладами можуть слугувати:
будівельні проекти;
організація масових заходів;
дизайн та маркетинг нового продукту;
організація злиття компаній;
. . .