Основные свойства простейших геометрических фигур

Геометрические фигуры
Геометрия – это наука о свойствах геометрических фигур. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие».

Всякую геометрическую фигуру мы представляем себе составленной из точек

В школе изучается геометрия, называемая евклидовой, по имени Евклида, создавшего руководство по математике под названием «Начала».
Евклид – древнегреческий ученый (III в. до н.э.)

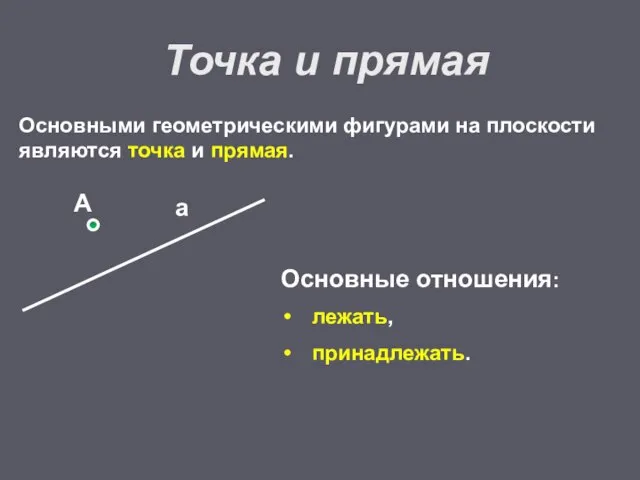
Основными геометрическими фигурами на плоскости являются точка и прямая.
Точка и прямая
Основные отношения:
лежать,
принадлежать.
А
а

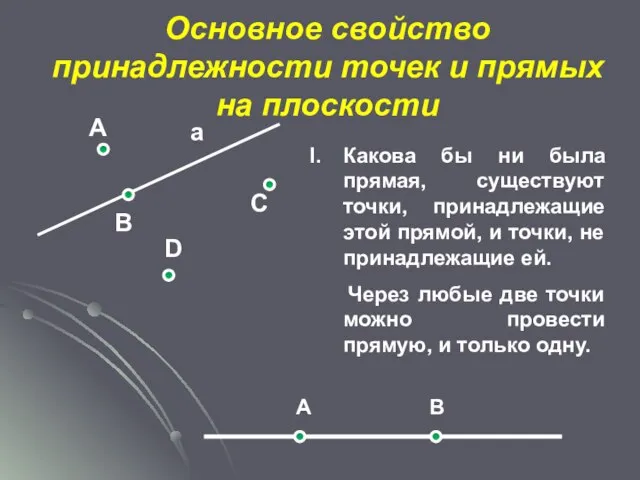
А
а
В
С
D
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Основное свойство принадлежности точек и прямых на плоскости
А В

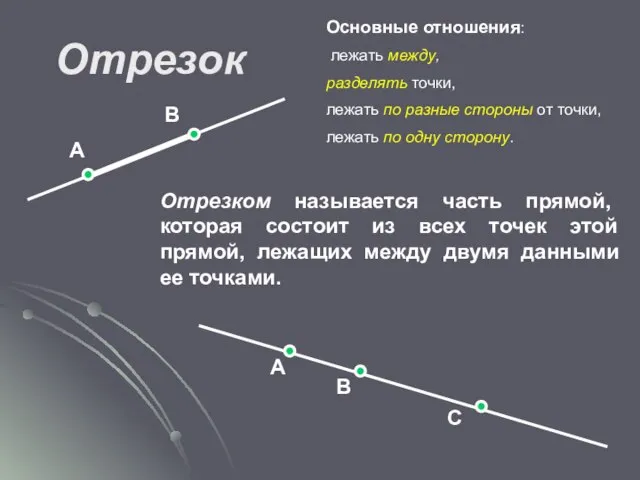
Отрезок
Основные отношения:
лежать между,
разделять точки,
лежать по разные стороны от точки,
лежать по одну сторону.
Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками.
А
В
А
В
С

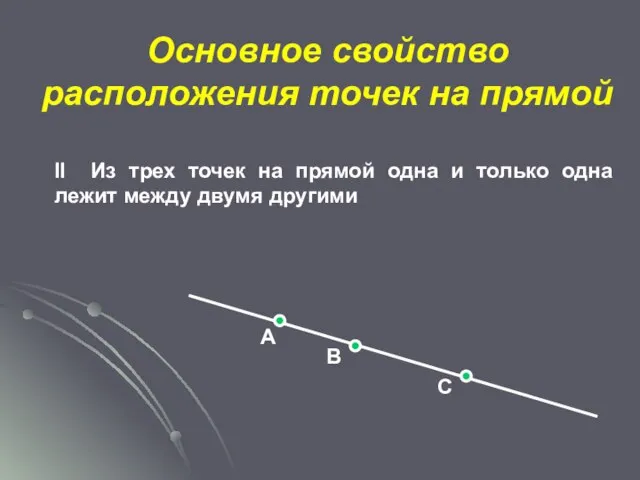
Основное свойство расположения точек на прямой
А
В
С
II Из трех точек на прямой одна и только одна лежит между двумя другими

Основное свойство измерения отрезков
Для измерения отрезков применяют различные измерительные инструменты
III Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
M N K

Полуплоскости
А
В
С
D
Основное свойство расположения точек относительно прямой на плоскости
IV Прямая разбивает плоскость на две полуплоскости.

Полупрямая
А Х У Z
Полупрямой или лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной ее точки
Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называют дополнительными.

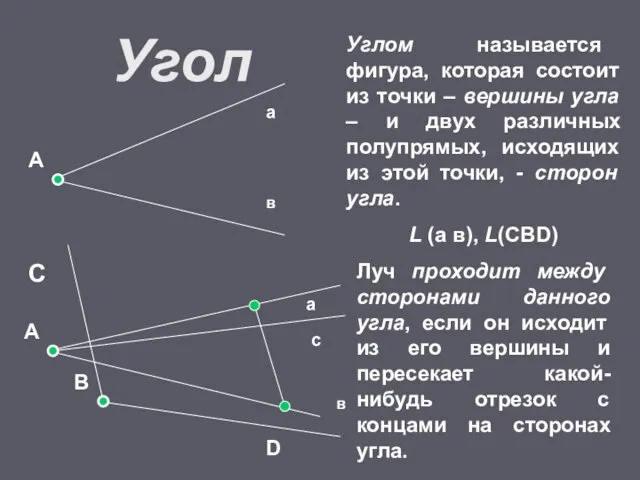
Угол
В
А
а
в
С
D
Углом называется фигура, которая состоит из точки – вершины угла – и двух различных полупрямых, исходящих из этой точки, - сторон угла.
L (а в), L(СВD)
А
а
в
с
Луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.

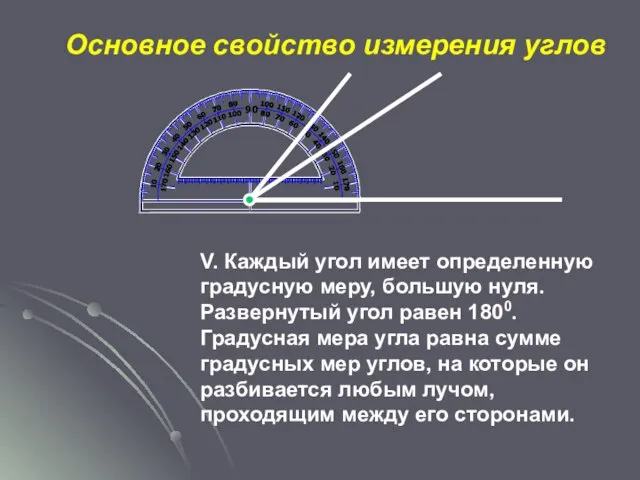
Основное свойство измерения углов
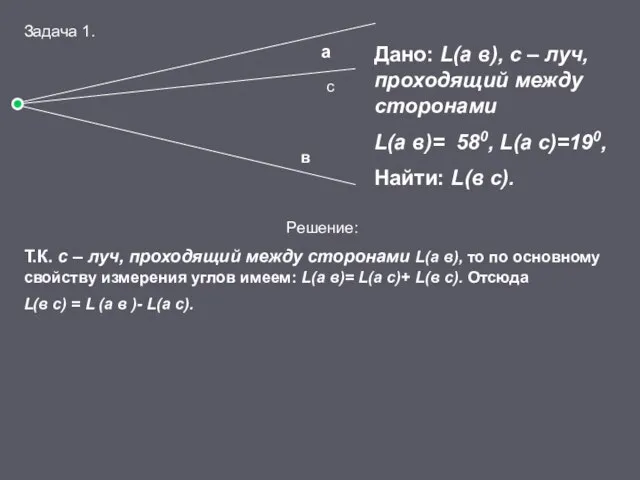
V. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 1800. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

а
в
с
Дано: L(а в), с – луч, проходящий между сторонами
L(а в)= 580, L(а с)=190,
Найти: L(в с).
Решение:
Т.К. с – луч, проходящий между сторонами L(а в), то по основному свойству измерения углов имеем: L(а в)= L(а с)+ L(в с). Отсюда
L(в с) = L (а в )- L(а с).
Задача 1.

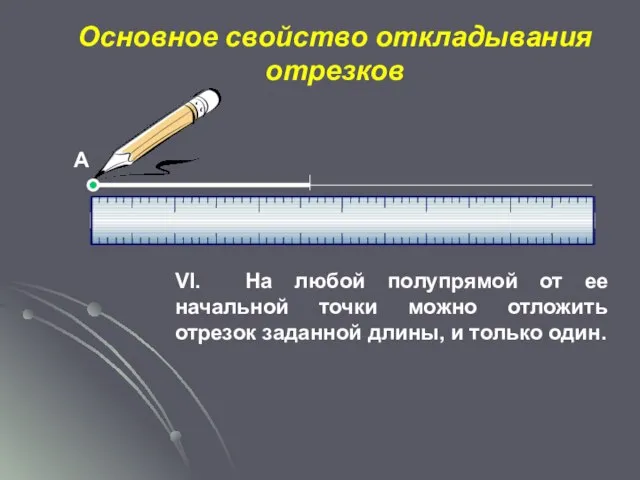
Основное свойство откладывания отрезков
VI. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.
А

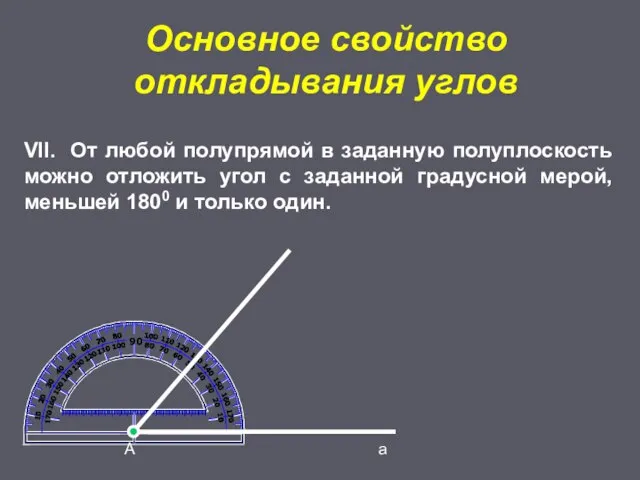
Основное свойство откладывания углов
А а
VII. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 1800 и только один.

Измерение углов на местности
Измерение углов на местности проводится с помощью специальных приборов. Простейшим из них является астролябия. Она состоит из двух частей: диска, разделенного на градусы, и вращающейся вокруг центра диска линейки (алидады). На концах алидады находятся два узких окошечка, которые используются для установки ее в определенном направлении.

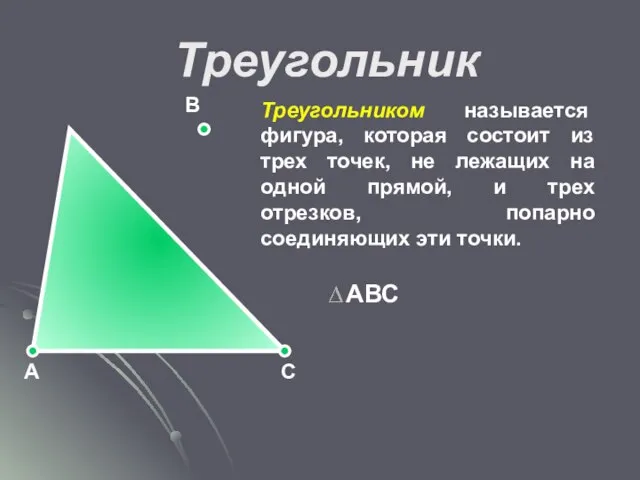
Треугольник
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
А С
В
АВС

А M
В С N K

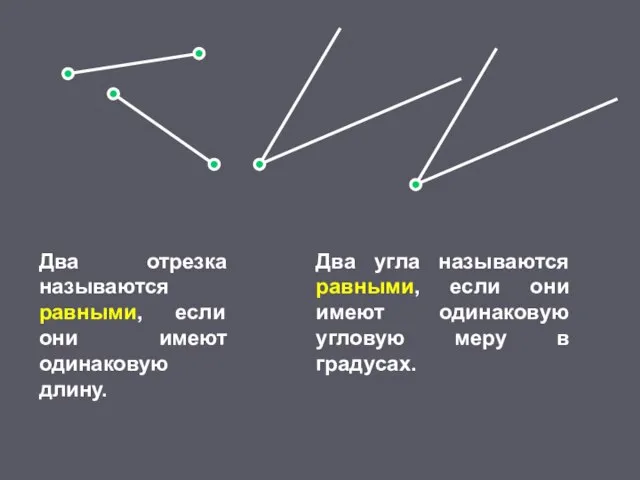
Два отрезка называются равными, если они имеют одинаковую длину.
Два угла называются равными, если они имеют одинаковую угловую меру в градусах.

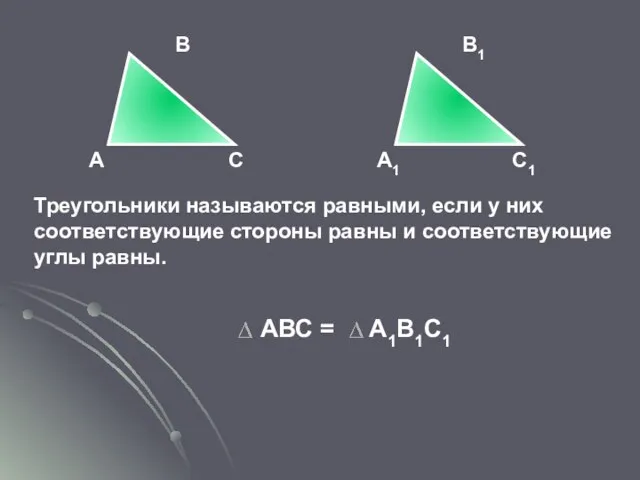
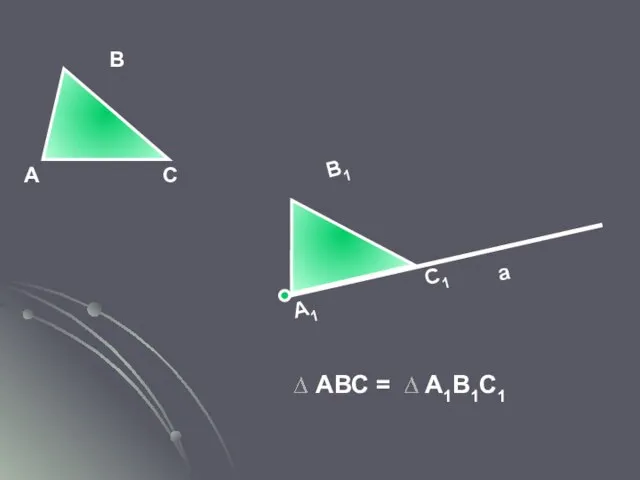
А С
В
А1 С1
В1
Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны.
АВС = А1В1С1

Основное свойство существования треугольника равного данному
VIII. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной прямой.
Существование треугольника равного данному

А С
В
А1 С1
В1
АВС = А1В1С1
а

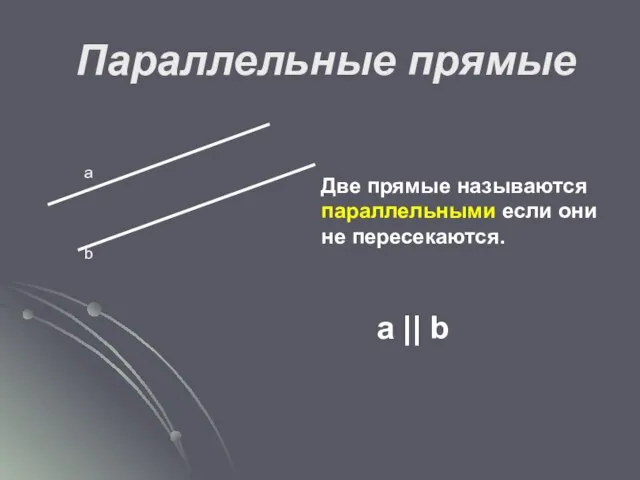
Параллельные прямые
а
b
Две прямые называются параллельными если они не пересекаются.
а || b

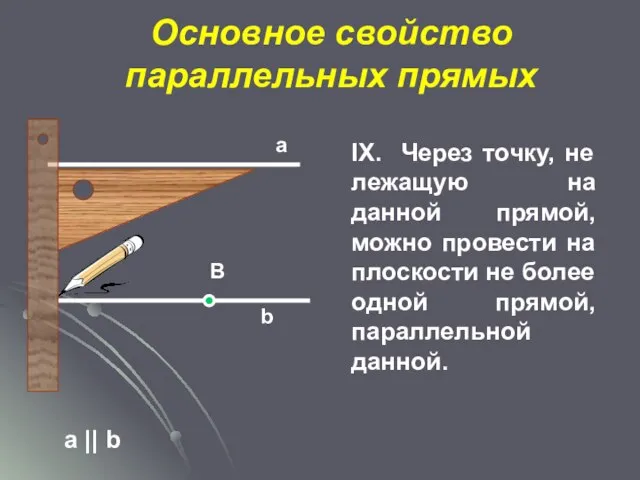
Основное свойство параллельных прямых
а || b
а
В
b
IX. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

В развитии геометрии важную роль сыграла аксиома, которая в «Началах…» Евклида называлась пятым постулатом (аксиома параллельности прямых).
Много веков усилия большого числа ученых были направлены на доказательство этой аксиомы. Это объяснялось тем, что число аксиом стремились свести к минимуму. Ученые думали, что пятый постулат можно доказать как теорему, опираясь на остальные аксиомы.
В конце XVIII в. у некоторых геометров возникла мысль о невозможности доказать V постулат. Решение этого вопроса было найдено великим русским математиком Николаем Ивановичем Лобачевским (1792-1856 гг).
Лобачевский предпринял попытку доказать это утверждение от противного: он предположил, что через точку, не лежащую на данной прямой можно провести несколько прямых, не пересекающих данную.

Лобачевский не получил противоречивых выводов. На основании этого им был сделан замечательный вывод: можно построить другую геометрию, отличную от геометрии Евклида.
Сообщение об открытии новой геометрии было сделано Лобачевским в 1826 г.
Современной наукой установлено, что евклидова геометрия лишь приближенно, хотя и с очень большой точностью, описывает окружающее нас пространство, а в космических масштабах она имеет заметное отличие от геометрии реального пространства. Бурное развитие математики в XIX в привело к созданию выдающимся немецким математиком Б.Риманом (1826-1866 г.г) новой геометрии.

Аксиомы.
Теоремы и доказательства
Утверждения, принимаемые без доказательств, называются аксиомами.
Утверждение, истинность которого необходимо доказать, называется теоремой.
Доказательство – это рассуждения, опирающееся на аксиомы и ранее доказанные теоремы, устанавливающее истинность данного факта. Никакими другими свойствами фигур, даже если они нам кажутся очевидными, пользоваться нельзя.
При доказательстве разрешается пользоваться чертежом как геометрической записью того, что мы выражаем словами.
Определение – словесное описание геометрического объекта, объясняющее, что это такое.