Содержание
- 2. История логики… Аристотель 384-322 г. до н.э. Рене Декарт 1596-1650 г.г. Вильгельм Лейбниц 1646-1716 г.г. Джордж
- 3. ЛОГИКА – это наука правильно рассуждать, наука о формах и законах человеческого мышления ГЛАВНАЯ ЗАДАЧА ЛОГИКИ
- 4. ПОНЯТИЕ – мысль, в которой «схватывается» сущность предметов, их внутреннее содержание. СУЖДЕНИЕМ (ВЫСКАЗЫВАНИЕМ) называется всякое утверждение
- 5. Единственная характеристика каждого высказывания есть истинность или ложность. Эта характеристика называется значением истинности данного высказывания. А
- 6. Суждениями не являются вопросительные, восклицательные предложения и ПРЕДИКАТЫ (выражения о переменных). «5 + Х = 12»,
- 7. ЧАСТНЫЕ суждения выражают конкретные (частные) факты. ОБЩИЕ суждения характеризуют свойства групп объектов или явлений. Суждение считается
- 8. Какие из предложений являются суждениями и каково значение их истинности: «сидит и смотрит» «сумма внутренних углов
- 9. Укажите, какие из суждений являются частными, а какие общими: «(x + y) (x – y) =
- 10. РАССУЖДЕНИЕ – это цепочка взаимосвязанных суждений, фактов и общих положений, получаемых из других суждений по определенным
- 11. Умозаключение по аналогии - это знание, полученное из рассмотрения какого-либо объекта, переносимое на менее изученный, сходный
- 12. «Квадрат – это равносторонний и равноугольный параллелограмм» «Квадрат – это равносторонний прямоугольник» «Квадрат – это равноугольный
- 13. Индукция («наведение» – с лат.) – это правило вывода умозаключений при переходе от частных суждений к
- 14. Пример Саша сказал: «У Димы больше 1000 книг». Коля возразил: «Нет, книг у него меньше». «Одна-то
- 15. Законы классической логики Закон тождества: каждый из предметов, о котором идет речь в рассуждениях и выводах,
- 16. 5. Закон достаточных оснований (Г. Лейбниц): любое утверждение должно предполагать наличие аргументов фактов, достаточных для его
- 18. Скачать презентацию















 Источники и методы финансирования бизнес-плана
Источники и методы финансирования бизнес-плана Подготовка в сфере информационных технологий
Подготовка в сфере информационных технологий Коммуникационная политика в международном маркетинге
Коммуникационная политика в международном маркетинге Презентация на тему Основы логики
Презентация на тему Основы логики  Вопросы семинара по теме: Производство вискозных нитей
Вопросы семинара по теме: Производство вискозных нитей Пути совершенствования переработки продукции кролиководства
Пути совершенствования переработки продукции кролиководства Презентация на тему Компьютерная графика
Презентация на тему Компьютерная графика  Программы и файлы
Программы и файлы Агрессивное поведение
Агрессивное поведение Новое время - торжество Европы (4 класс)
Новое время - торжество Европы (4 класс) Освіта в Украині
Освіта в Украині 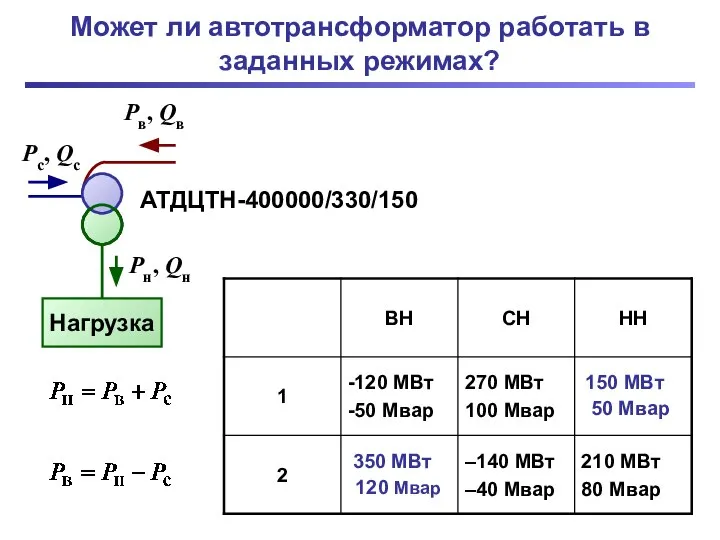 Может ли автотрансформатор работать в заданных режимах. Контрольная работа, пример 2
Может ли автотрансформатор работать в заданных режимах. Контрольная работа, пример 2 Работа ученицы 11 «А» Ноландт Татьяны
Работа ученицы 11 «А» Ноландт Татьяны Мотивация барменов
Мотивация барменов Институциональные модели капитализма
Институциональные модели капитализма  О шестиугольных снежинках от Кеплера до наших дней
О шестиугольных снежинках от Кеплера до наших дней Уважаемые коллеги! Поздравляем с наступающим новым годом и Рождеством!Желаем вам радостных дней,Здоровья, успехов, надежных друз
Уважаемые коллеги! Поздравляем с наступающим новым годом и Рождеством!Желаем вам радостных дней,Здоровья, успехов, надежных друз Сравнение открытой и закрытой форм тестирования
Сравнение открытой и закрытой форм тестирования -пропаганда здорового образа жизни; -определение лучших команд классов; -определение уровня двигательной активности школьников.
-пропаганда здорового образа жизни; -определение лучших команд классов; -определение уровня двигательной активности школьников. Возможные причины моббинга
Возможные причины моббинга ФОРМЫ ГОСУДАРСТВЕННОГО УСТРОЙСТВА И ПОЛИТИЧЕСКИЕ РЕЖИМЫ
ФОРМЫ ГОСУДАРСТВЕННОГО УСТРОЙСТВА И ПОЛИТИЧЕСКИЕ РЕЖИМЫ 1급 4과
1급 4과 С мамой в спорт
С мамой в спорт Фон в портрете
Фон в портрете И.А. Крылов. Жанр басни в творчестве Крылова
И.А. Крылов. Жанр басни в творчестве Крылова 2.7(9)_А201.7250.101Э3_Лист 3 из 9_fr
2.7(9)_А201.7250.101Э3_Лист 3 из 9_fr Т.И Р-21 Рчков
Т.И Р-21 Рчков ООО «Глория» | www.slavagloria.ru
ООО «Глория» | www.slavagloria.ru