Содержание
- 2. Курс «Основы статистики » для студентов факультета «Связи с общественностью» рассчитан на то, чтобы дать представление
- 3. литература Шолохович Ф.А. Высшая математика в кратком изложении. Екатеринбург, УрГУ, 2003 Турецкий В.Я. Высшая математика. Екатеринбург,
- 4. Шкалы измерений Номинальная. Позволяет различать предметы, например по цвету Дихотомическая. Ранговая. Позволяет упорядочить предметы Интервальная Относительная
- 5. Случайные события Событие называется детерминированным, если в результате опыта оно происходит или не происходит наверняка. В
- 6. События A и B называются несовместными, если появление одного исключает появление другого. Событие B следует из
- 7. Пусть случайный эксперимент проводится раз n, и событие A произошло m раз. Тогда говорят, что относительная
- 8. Алгебра событий Суммой двух событий A и B называется событие A+B, состоящее в том, что произошло
- 10. 1. Если события несовместны, то вероятность суммы событий равна сумме вероятностей: P(A+B) = P(A) + P(B)
- 11. Примеры. 1. Подбрасываем кубик. Всего исходов 6. Какова вероятность, что выпадет четное число? Благоприятны исходы 2,
- 12. Решение. Могут произойти следующие события: А1 промах в 1 выстреле, А2 промах во 2, А3 -
- 13. Разностью событий A и B называется событие A - B , состоящее в том, что произошло
- 14. Комбинаторика Например, число перестановок из 6 предметов 1х2х3х4х5х6=120. Число расстановок из 6 предметов на 4 места
- 15. Например, число перестановок из 6 предметов 1х2х3х4х5х6=720. Число сочетаний из 6 предметов по 4
- 16. Классическое определение Свойства вероятности. I. Для любого случайного события А 0≤P(A) ≤1 2. Пусть события A
- 17. Пример. В корзине 15 шаров. Из низ 5 белых и 10 черных. Какова вероятность вытащить 3
- 18. Пример. Из колоды в 36 карт вытаскиваем 4. Какова вероятность, что среди них 2 короля? Решаем
- 19. Вероятность суммы событий Даны два события A и B. Подсчитаем вероятность суммы событий по классической схеме.
- 20. Отсюда находим формулу вероятности суммы событий Пример. Два стрелка независимо стреляют по мишени. Первый попадает с
- 21. Условная вероятность Пусть известно, что в результате эксперимента произошло событие B. Зная это, мы хотим подсчитать
- 22. Свойства условной вероятности. 1. P(A|A)=1 . 2. Если B⊂Α , то P(A|B)=1. 3. Для любого события
- 23. Формула полной вероятности Теорема. Пусть события B1, B2, . . ., Bn попарно несовместны и событие
- 24. Пример. Имеется 3 группы корзин. Корзин типа B1 – 5 Корзин типа B2 – 3 Корзин
- 25. Формула Байеса Теорема. Пусть события B1, B2, . . ., Bn попарно несовместны и событие A
- 26. Пример Те же самые условия. Случайно извлечен белый шар. Какова вероятность, что он извлечен из первой
- 27. Схема испытаний Бернулли Пусть в результате некоторого случайного испытания может произойти или не произойти определенное событие
- 28. Формула Бернулли вероятности k успехов в n независимых испытаниях. В серии из n испытаний должно одновременно
- 29. Пример. Подбрасываем 10 раз кубик. Какова вероятность, что пятерка выпадет ровно 4 раза? Решение. Схема испытаний
- 30. Задача 2. Какова вероятность, что число успехов будет от k1 до k2? Очевидно, что цепочки с
- 31. Локальная теорема Лапласа Если вероятность p появления события A в каждом испытании постоянна и отлична от
- 32. Интегральная теорема Лапласа Если вероятность p появления события A в каждом испытании постоянна и отлична от
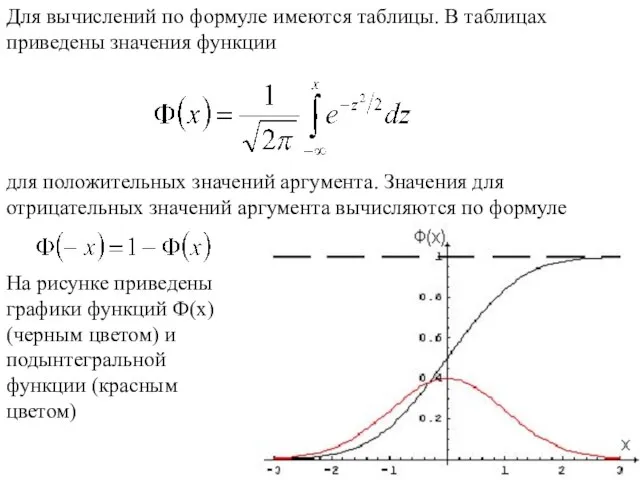
- 33. Для вычислений по формуле имеются таблицы. В таблицах приведены значения функции для положительных значений аргумента. Значения
- 34. Если -x1=x2=x, то справедлива формула
- 35. Пример 1. Какова вероятность, что из 100 подбрасываний кубика четверка выпадет ровно 30 раз. n=100, m=30,
- 36. Пример 2. Какова вероятность, что из 100 подбрасываний кубика 4 выпадет от m1=15 до m2=25 раз.
- 37. Задача 3 . Сколько раз нужно подбросить кубик, чтобы частота отличалась от вероятности не более чем
- 38. Подставив числа, получим уравнение относительно n По таблице ищем значение аргумента функции Лапласа такое, что ее
- 39. Конечная случайная величина Часто исход случайного эксперимента выражается некоторым числом. Когда каждому элементарному исходу случайного эксперимента
- 40. Случайная величина, принимающая конечное число значений, называется конечной случайной величиной. Пусть пространство элементарных исходов конечно: Ω=•ω1,ω2,...,ωn
- 41. Такое вероятностное пространство можно представить с помощью таблицы Функцию ξ(ω), заданную на конечном числе аргументов, также
- 42. Поэтому таблица часто отождествляется с самой случайной величиной и называется законом распределения конечной случайной величины. Часто
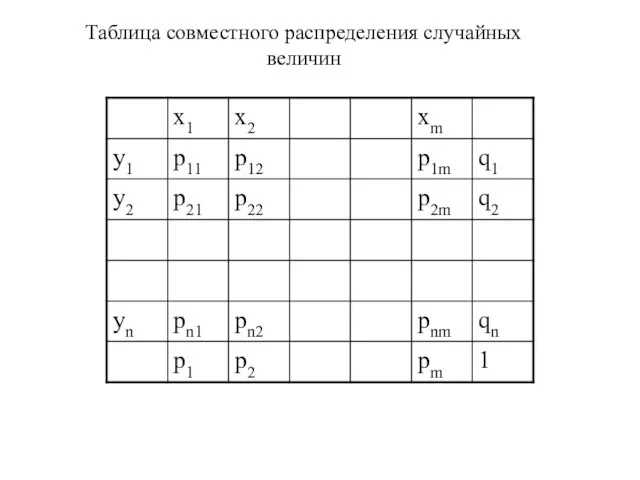
- 43. Совместное распределение случайных величин Пусть заданы две конечные случайные величины: Событие •ξ=xi••η=yj} состоит в том, что
- 44. Таблица совместного распределения случайных величин
- 45. Две конечные случайные величины называются независимыми, если события •ξ=xi• и •η=yj} независимы при всех i=1,2,. .
- 46. Произведением этих случайных величин называется случайная величина ξ η, значениями которой являются всевозможные произведения xiyj с
- 47. В результате получим таблицу Этот результат можно обобщить на любое число слагаемых. Теорема. Пусть ξ1, ξ2,
- 48. Математическое ожидание Математическим ожиданием конечной случайной величины называется число Понятие математического ожидания упрощенно можно представить иначе.
- 49. Например, при бросании кубика вероятность выпадения каждой грани равна 1/6. Тогда математическое ожидание числа очков равно
- 50. Математическое ожидание обладает следующими свойствами. 1. Математическое ожидание постоянной равно ей самой: 2. Если случайная величина
- 51. 5. Для любой случайной величины справедливо равенство Операция вычитания математического ожидания из случайной величины называется центрированием
- 52. Дисперсия Дисперсией конечной случайной величины ξ называется число по определению математического ожидания, дисперсия вычисляется по следующей
- 53. Свойства дисперсии Дисперсия любой случайной величины неотрицательна Dξ>0 При этом Dξ=0 тогда и только тогда, когда
- 54. 5. Дисперсия равна "среднему квадрата минус квадрат среднего": Дисперсия биномиальной случайной величины. Вычисление проведем по той
- 55. Случайная величина называется стандартизованной (по отношению к ξ) или просто стандартизацией ξ Стандартизованная случайная величина имеет
- 56. Задача. Проводится лотерея. Разыгрывается 50 билетов по 1 рублю. Известно, что среди билетов 1 выигрывает 30
- 57. Коэффициент корреляции Ковариацией двух случайных величин ξ и η (или ковариацией между ξ и η) называется
- 58. Следующее свойство важно при оценке степени зависимости двух случайных величин. 5. Если случайные величины ξ и
- 59. свойства коэффициента корреляции: 2. Коэффициенты корреляции между ξ и η и между их стандартизациями совпадают 1.
- 60. Примеры. Даны таблицы распределения. Найти коэффициенты корреляции Вычислительная формула
- 61. Mx=0, Dx=2, MY=1, DY=2 MXY=-2, R=-1 Mx=0, Dx=2, MY=3.8, DY=3.46 MXY=2.6, R=0.9884 Mx=0, Dx=2, MY=2, DY=2.8
- 62. Функция распределения Функция действительной переменной называется функцией распределения случайной величины ξ . Свойства функции распределения 1.
- 63. 6. Функция распределения непрерывна слева, то есть
- 64. 7. Для любой непрерывной случайной величины 8. Функция распределения непрерывной случайной величин имеет вид
- 65. Функция неотрицательна при всех x 2. Условие нормировки. Справедливо равенство Свойства плотности функции распределения 3. В
- 66. Математическим ожиданием непрерывной случайной величины называется число (если соответствующий интеграл существует). Дисперсия вычисляется через интеграл: (если
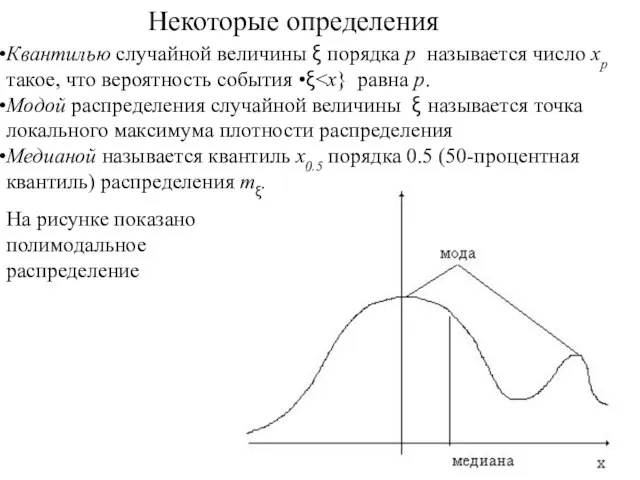
- 67. Квантилью случайной величины ξ порядка p называется число xp такое, что вероятность события •ξ Модой распределения
- 68. Биномиальное распределение где Распределение Пуассона. Получается как предельное при очень большом числе испытаний маловероятных событий.
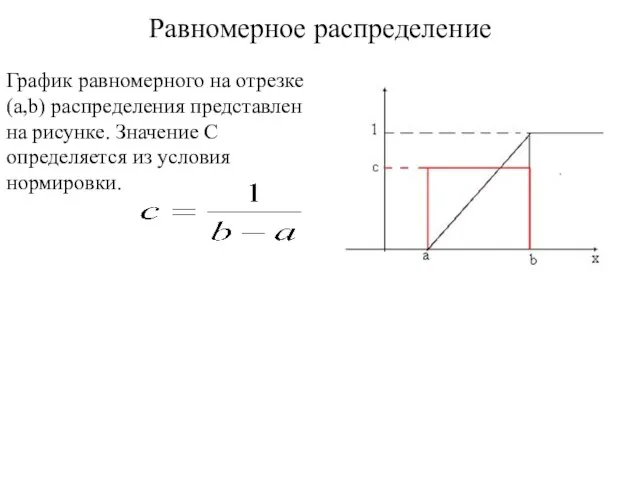
- 69. Равномерное распределение График равномерного на отрезке (a,b) распределения представлен на рисунке. Значение C определяется из условия
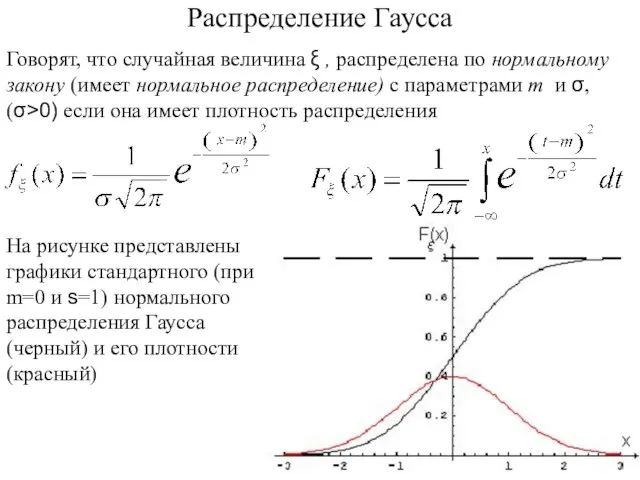
- 70. Говорят, что случайная величина ξ , распределена по нормальному закону (имеет нормальное распределение) с параметрами m
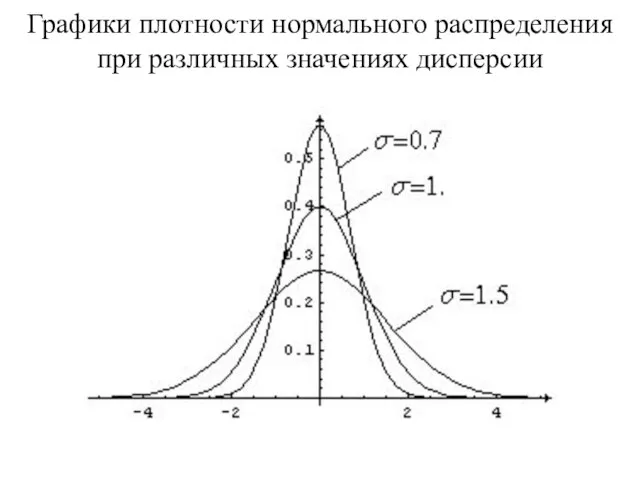
- 71. Графики плотности нормального распределения при различных значениях дисперсии
- 72. Свойства нормального распределения график симметричен относительно прямой x=m; функция достигает максимума в точке x=m; график приближается
- 73. Пусть ξ~Ν(m,σ). Тогда квантиль xp случайной величины ξ связана с квантилью стандартного нормального распределения следующим соотношением:
- 74. Законы больших чисел Теорема Бернулли
- 75. Центральная предельная теорема Ляпунова Пусть случайные величины X1, X2, …, Xn независимы, одинаково распределены с математическим
- 76. Статистика Генеральной совокупностью называется вся совокупность исследуемых объектов Выборочной совокупностью или просто выборкой называют совокупность случайно
- 77. Простой случайный отбор – объекты извлекают по одному из всей генеральной совокупности Типический отбор - объекты
- 78. Выборка и ее обработка Совокупность пар (zi, ni ) называют статистическим рядом выборки. Часто его представляют
- 79. Удобнее всего разбивать на равные интервалы. При этом считается, что правая граница интервала принадлежит следующему интервалу.
- 80. Пример Дана выборка 0,0473 0,0543 0,0561 0,0989 0,1107 0,1112 0,1204 0,1647 0,2030 0,2138 0,2147 0,2463 0,2725
- 81. Проведем группировку. Разобьем отрезок на 10 полуинтервалов [0,0.1),[0.1,0.2),…[0.8,0.9),[0.9,1.0]. Подсчитаем, сколько элементов выборки попало в каждый интервал
- 82. Эмпирическая функция распределения Это распределение называется выборочным, или эмпирическим, распределением. Как и для любой конечной случайной
- 84. Оценки параметров распределения Точечные оценки
- 85. Индекс п в обозначении оценки напоминает, что она получена по выборке объема n, «звездочка» показывает, что
- 87. Несмещенная оценка называется наиболее эффективной (или просто эффективной), если она имеет минимальную дисперсию среди всех несмещенных
- 88. ОЦЕНКА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- 89. Поскольку каждое значение из выборки есть случайная величина с функцией распределения, то вероятность успеха равна p=F(x)
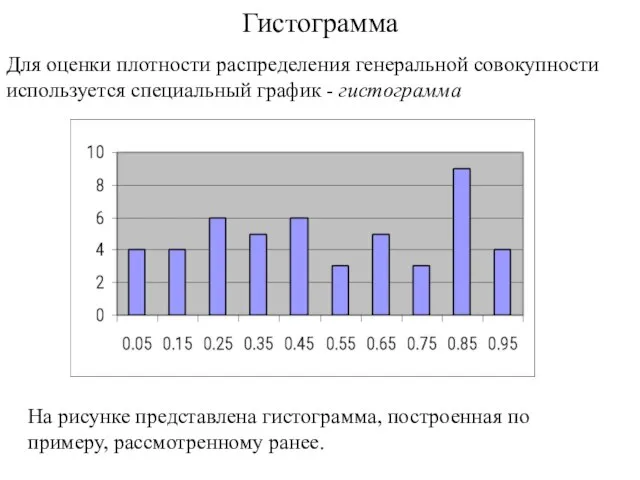
- 90. Гистограмма Для оценки плотности распределения генеральной совокупности используется специальный график - гистограмма На рисунке представлена гистограмма,
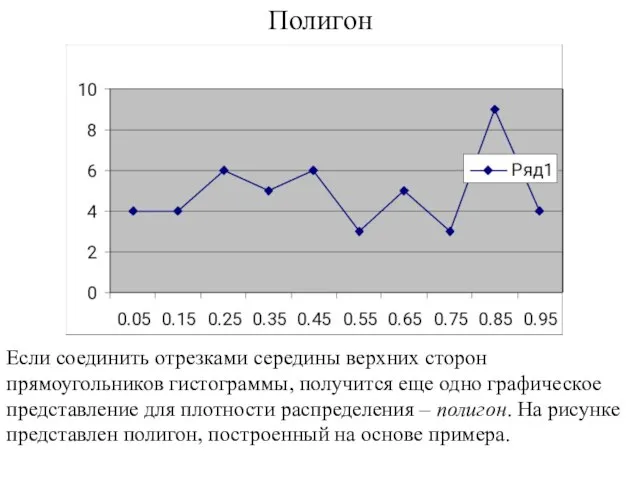
- 91. Полигон Если соединить отрезками середины верхних сторон прямоугольников гистограммы, получится еще одно графическое представление для плотности
- 92. Точечная оценка математического ожидания Выборочное среднее дает несмещенную и состоятельную оценку математического ожидания
- 93. Точечная оценка дисперсии Вычислим математическое ожидание выборочной дисперсии. Для этого преобразуем выражение для s2 (через М
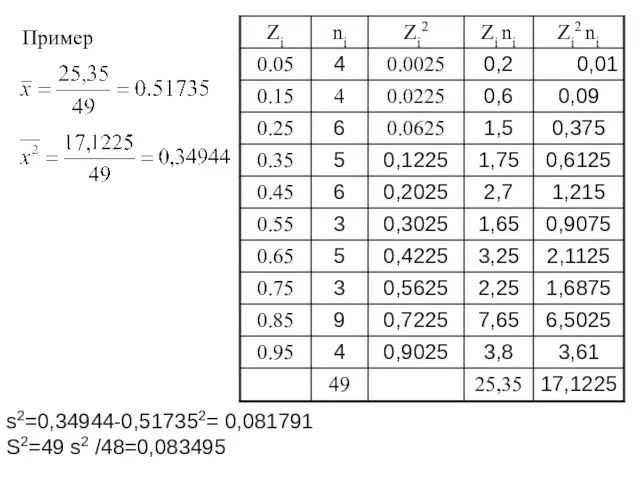
- 95. Приведенное выражение дает состоятельную несмещенную оценку дисперсии генеральной совокупности Для вычисления выборочной дисперсии можно вывести более
- 96. Пример s2=0,34944-0,517352= 0,081791 S2=49 s2 /48=0,083495
- 97. Выборочные мода, медиана, квантили Выборочные мода, медиана и квантиль легко определяются по упорядоченной, но не сгруппированной
- 98. Интервальные оценки Интервальная оценка – некоторый интервал [a,b]. По заданной выборке мы должны найти a(x1,x2,…,xn) и
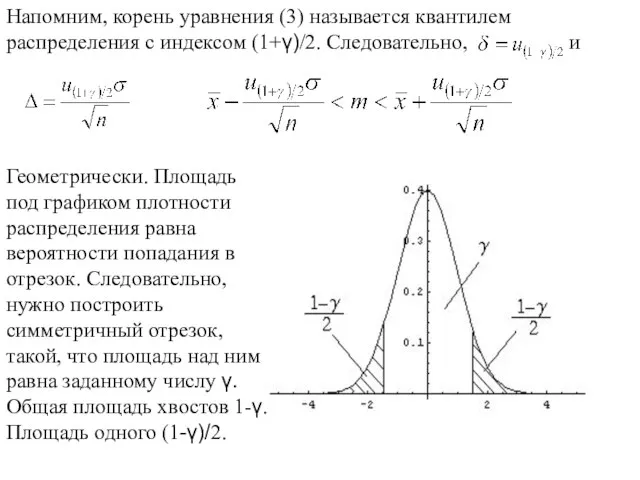
- 99. Доверительный интервал математического ожидания Случай 1. Считаем, что известна дисперсия генеральной совокупности σ2.
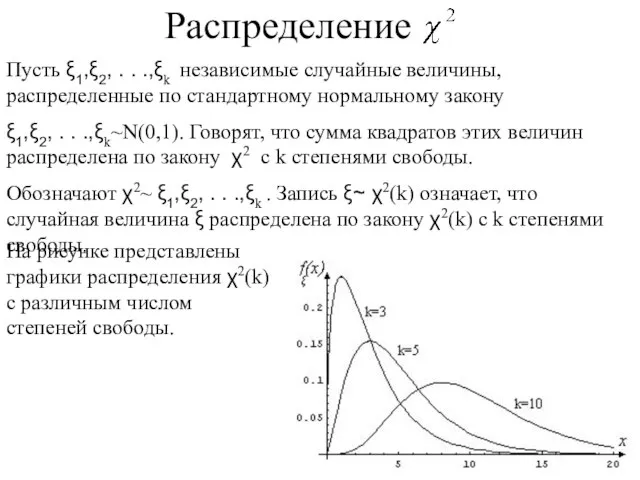
- 102. Пусть ξ1,ξ2, . . .,ξk независимые случайные величины, распределенные по стандартному нормальному закону ξ1,ξ2, . .
- 103. Свойства распределения χ2 . Случайная величина имеет нулевую плотность распределения при x≤0. При большом числе степеней
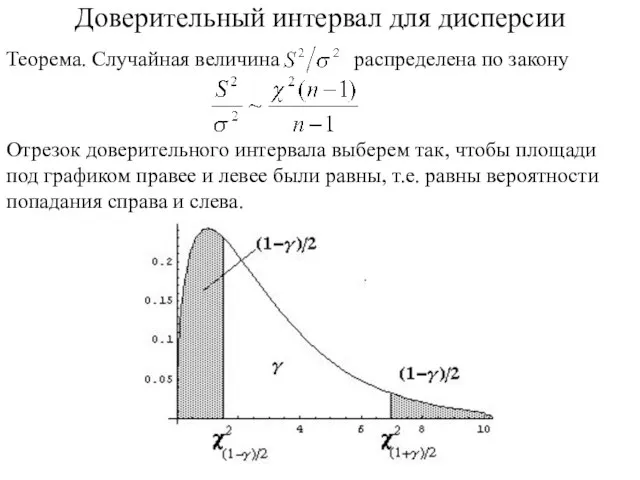
- 104. Доверительный интервал для дисперсии
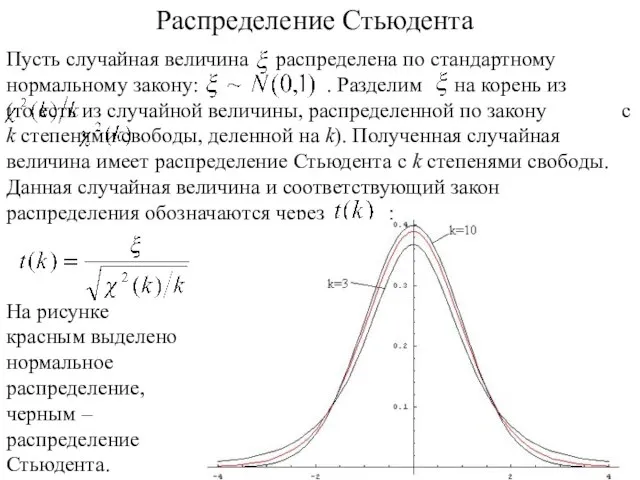
- 106. Распределение Стьюдента На рисунке красным выделено нормальное распределение, черным – распределение Стьюдента.
- 107. Свойства распределения Стьюдента Распределение Стьюдента симметрично, причем Mt(k) = 0. При больших k распределение Стьюдента близко
- 108. Доверительный интервал математического ожидания. Случай 2. Случайная величина U распределена по нормальному закону
- 109. Пример m=0.51735, σ=0,288955, n=49. После вычислений получим 0,0809074. Интервал будет 0.51735- 0,0809074 0,4364426
- 110. Пример. Интервал для дисперсии Находим интервал 0,056131 После вычислений получим 0.51735- 0,082992 0,434358
- 111. Основы теории проверки статистических гипотез Статистической гипотезой называется предположение относительно параметров или вида распределения наблюдаемой случайной
- 112. Например: выдвигается гипотеза о значении математического ожидания H0 : m=a Возможные альтернативные H1: m≠a, m>a, m
- 113. Формирование решающего правила опирается на ту же идею, которая используется при построении доверительных интервалов. Ищется случайная
- 114. Построение решающего правила на основе критерия значимости можно разбить на следующие основные шаги. 1. Сформировать нулевую
- 115. 7. Принять решение: • если Zs∈Vc , гипотеза H0 отклоняется (то есть принимается гипотеза H1): •
- 116. Пример: проверка гипотезы о математическом ожидании
- 117. Пример 2. Иной вариант альтернативной гипотезы
- 118. Ошибки при проверке статистических гипотез Принятие решения на основе статистического критерия носит случайный характер. Возможны следующие
- 119. В этой ситуации выборочное значение попало в область принятия решения, тогда как гипотеза на самом деле
- 120. Проверка гипотезы о функции распределения
- 121. Понятие о факторном анализе Пусть результаты наблюдений составляют k независимых выборок (групп), полученных из k нормально
- 124. Скачать презентацию









































































![Проведем группировку. Разобьем отрезок на 10 полуинтервалов [0,0.1),[0.1,0.2),…[0.8,0.9),[0.9,1.0]. Подсчитаем, сколько элементов выборки](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/410160/slide-80.jpg)













![Интервальные оценки Интервальная оценка – некоторый интервал [a,b]. По заданной выборке мы](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/410160/slide-97.jpg)




















 совместно с Театром праздника «Солнечный зайчик»
совместно с Театром праздника «Солнечный зайчик» ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс
ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс Презентация на тему Врожденные и приобретенные программы поведения
Презентация на тему Врожденные и приобретенные программы поведения Презентация
Презентация ПРОЕКТНАЯ РАБОТА
ПРОЕКТНАЯ РАБОТА к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич
к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич Культура Руси в 10 – 13 веках
Культура Руси в 10 – 13 веках Болгария в 20-30-е годы
Болгария в 20-30-е годы Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя
Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя Приготовление завтрака
Приготовление завтрака «Инвестиционная политика муниципального образования на современном этапе»02.02.2012
«Инвестиционная политика муниципального образования на современном этапе»02.02.2012 Работа академии по направлению научно-технического творчества молодежи
Работа академии по направлению научно-технического творчества молодежи «Трудные» дети и их проблемы.
«Трудные» дети и их проблемы. Приемы расположения к себе. Самопрезентация
Приемы расположения к себе. Самопрезентация Автохимия. Завод автохимии
Автохимия. Завод автохимии Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года
Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года Евангелие от Матфея
Евангелие от Матфея Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов
Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов Аварийная аптечка для первой медицинской помощи
Аварийная аптечка для первой медицинской помощи Власть. Сила. Лекция 2
Власть. Сила. Лекция 2 Вітражі та шпроси
Вітражі та шпроси Моя будущая профессия - бухгалтер
Моя будущая профессия - бухгалтер Олимпиада үрләренә - баскычлап
Олимпиада үрләренә - баскычлап Общероссийские антидопинговые правила
Общероссийские антидопинговые правила Проектирование транспортно-грузовых комплексов
Проектирование транспортно-грузовых комплексов Определение размеров молекул октана
Определение размеров молекул октана Такси Лось
Такси Лось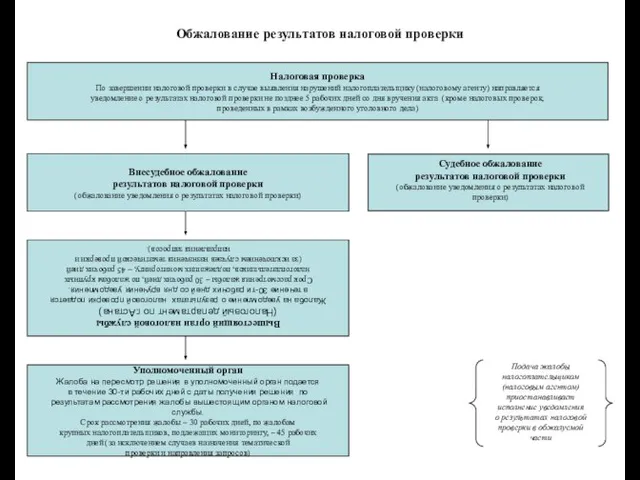 Обжалование результатов налоговой проверки
Обжалование результатов налоговой проверки