ОСНОВЫ ПРОГРАММИРОВАНИЯРаздел 2. Математические основы программированияПредставление чисел в ЭВМ

Рассматриваемые вопросы
Представление целых чисел
представление целых без знака
представление знаковых целых
Представление вещественных чисел
математическая основа представления вещественных чисел
современный стандарт представления вещественных чисел
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Представление чисел в ЭВМ
Особенности представления чисел в ЭВМ:
используется двоичная система счисления
ограниченное количество разрядов
в ЭВМ используется память, элементарная ячейка которой (бит) может иметь только 2 состояния (0 и 1). Поэтому отсутствует возможность хранить знаки: ( "+", "–" и "." ).
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Представление целых
чисел без знака
Пусть дана ячейка памяти, размер которой k бит.
Существует 2k всевозможных битовых наборов длины k.
Следовательно, всего возможно представить 2k различных чисел.
Существует всего (2k)! (количество перестановок из 2k элементов) способов закодировать беззнаковые числа битовыми наборами.
Среди всех теоретически возможных способов наиболее удобно использовать k-разрядную запись этого числа в двоичной системе счисления. Это позволяет естественным образом реализовать арифметические операции над числами.
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Представление целых
чисел без знака (примеры)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
17510 = 1010 11112
3610 = 10 01002

Представление знаковых целых
Отрицательные числа могут быть представлены в ЭВМ несколькими способами, выбор одного из которых оказывает влияние на реализацию арифметических операций.
Для представления знаковых целых чисел используются три способа:
1) прямой код;
2) обратный код;
3) дополнительный код.
Далее будут рассмотрены каждый из способов для десятичной и двоичной систем счисления (СС).
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Прямой код
(десятичная СС, 6 разрядов)
Это наиболее очевидный и близкий к естественному способ записи чисел.
Число формируется из одного знака и фиксированного количества разрядов (цифр), представляющих собой модуль числа. Например:
+123 456
-001 000
-012 123
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Прямой код
(двоичная СС, 8 бит)
При формировании прямого кода в двоичной СС старший бит (разряд) используется для хранения знака: 0 ~ "+", 1 ~ "-".
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
-10010 = 1110 01002, 10010 = 0110 01002
-3610 = 1010 01002, 3610 = 10 01002
знак
-100
-36

Обратный код
(десятичная СС, 6 разрядов)
Отрицательные числа также состоят из фиксированного числа разрядов и формируются путем дополнения каждого разряда до 9:
– 123 456 ↔ 876 543
1 ↔ 9 – 1 = 8
2 ↔ 9 – 2 = 7
3 ↔ 9 – 3 = 6
4 ↔ 9 – 4 = 5
5 ↔ 9 – 5 = 4
6 ↔ 9 – 6 = 3
– 123 456 = 999 999 – 123 456 = 876 543
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

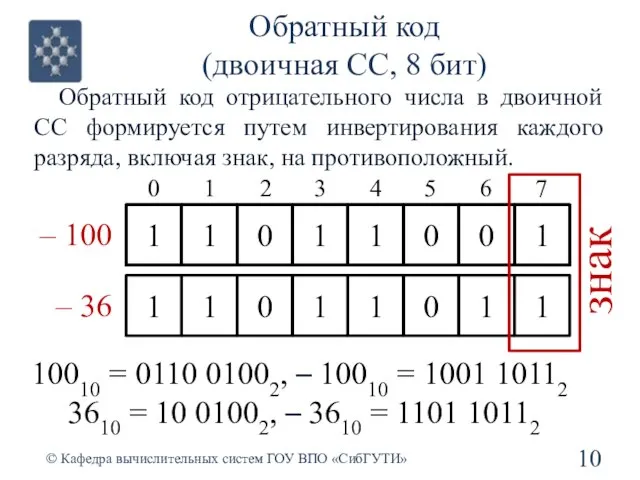
Обратный код
(двоичная СС, 8 бит)
Обратный код отрицательного числа в двоичной СС формируется путем инвертирования каждого разряда, включая знак, на противоположный.
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
10010 = 0110 01002, – 10010 = 1001 10112
3610 = 10 01002, – 3610 = 1101 10112
знак
– 100
– 36

Обратный код
(двоичная СС, 8 бит)
Для формирования обратного кода также может использоваться подход, аналогичный приведенному для десятичной СС:
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
– 10010 = 1111 11112 – 0110 01002 =
1001 10112

Дополнительный код
(десятичная СС, 6 разрядов)
Отрицательные числа в дополнительном коде представляются следующим образом:
– x = 0 – x = 1 000 000 – x
– 1 = 0 – 1 = 1 000 000 – 1 = 999 999
– 500 000 = 0 – 500 000 =
1 000 000 – 500 000 = 500 000
Диапазон: -500 000 до 499 999
(499 999 – 500 000)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Связь дополнительного и
обратного кода (дес. СС, 6 разрядов)
Дополнительный код
– х = 0 – х = 1 000 000 – х
– 1 = 0 – 1 = 1 000 000 – 1 =999 999
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Обратный код
– х = 0 – х = 999 999 – х
– 1 = 0 – 1 = 999 999 – 1 =999 998
<Доп. код> = <Обр. код> + 1

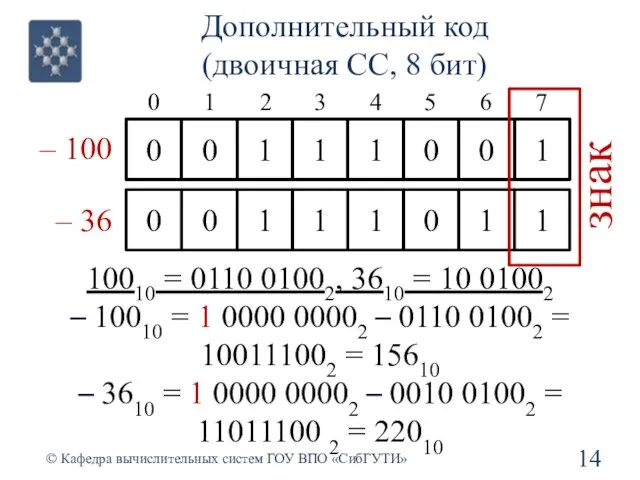
Дополнительный код
(двоичная СС, 8 бит)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
10010 = 0110 01002, 3610 = 10 01002
– 10010 = 1 0000 00002 – 0110 01002 =
100111002 = 15610
– 3610 = 1 0000 00002 – 0010 01002 =
11011100 2 = 22010
знак
– 100
– 36

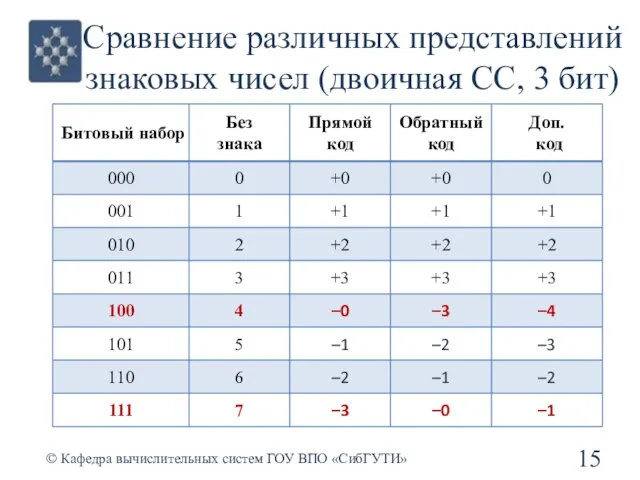
Сравнение различных представлений знаковых чисел (двоичная СС, 3 бит)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Сложение и вычитание
целых чисел без знака
Сложение и вычитание k-разрядных целых чисел без знака происходит по обычным для позиционных систем счисления правилам. Примеры (для k = 3):
0012 + 1002 = 1012;
1012 − 0102 = 0112.
Ситуации, когда уменьшаемое меньше вычитаемого или когда результат суммы не умещается в k разрядов, считаются ошибочными и должны отслеживаться устройством компьютера.
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Обработка переполнения
при сложении целых чисел без знака
Если при сложении двух k-разрядных чисел возникает (k+1)-й разряд, то он будет отброшен. Пример (для k = 3):
510 + 410 =
1012 + 1002 = 10012 =
0012 = 110
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Сложение целых знаковых чисел в дополнительном коде
Сложение k-разрядных знаковых чисел производится аналогично алгоритму для целых чисел без знака.
Складываются все разряды, включая знаковый
Если в результате сложения возникает (k+1)-й разряд, то он отбрасывается.
Для k = 3:
+310 + (−110) = 0112 + 1112 = 10102 =>
0102 = +210.
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Вычитание целых знаковых чисел в дополнительном коде
При вычитании также используется аналогичный алгоритм, однако если уменьшаемое меньше вычитаемого, к двоичному коду уменьшаемого слева приписывается единица (т.е. добавляется 2k ) и только после этого производится вычитание (такой способ называется вычитание по модулю 2k).
Для k = 3:
110 − 310 = 0012 − 0112 =>
10012 − 0112 = 1102 = −210.
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Сложение и вычитание
по модулю 2k
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Вещественные числа
В памяти ЭВМ не предусмотрено специальных средств для запоминания десятичной точки.
Существует два способа представить вещественное число в виде десятичной дроби:
1. Явно указав позицию запятой внутри числа: 23.456, 0.0098;
2. Научный, с помощью степени основания 10: 2.3456*101, 0.98*10-2
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Вещественные числа с
фиксированной точкой
Данное представление соответствует первому варианту записи вещественных чисел.
Положение точки внутри байта (байтов) задается фиксировано, например: для хранения используется 1 байт, пусть биты с 0 по 4 – целая часть, а биты с
5 по 7 – дробная часть:
0000 0.000
0000 0.001
0000 0.010
.....
1111 1.110
1111 1.111
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Вещественные числа с
фиксированной точкой
(недостатки)
1) Малый диапазон значений.
2) Неэффективное использование памяти при работе только с малыми числами или только с большими числами.
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Вещественные числа с
плавающей точкой
p-разрядным числом с плавающей точкой по основанию b с избытком q называется пара величин (e, f), которой соответствует значение:
( e, f ) = f ⋅ b(e – q)
e – порядок – беззнаковое целое число, изменяющаяся в определенном промежутке.
f – мантисса – знаковое вещественное число с фиксированной точкой, при этом:
| f | < 1,
т.е. разделяющая точка находится в крайней слева позиции
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Научная форма записи
вещественных чисел
Научная форма записи вещественных чисел позволяет представить одно и то же число множеством различных способов.
Например, постоянная Планка h = 6.6261⋅10-27 может быть записана одним из следующих способов:
66.261⋅10-28
66261⋅10-31
0.66261⋅10-26
0.00066261⋅10-23
…
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

Нормализованная форма
Представление информации в ЭВМ требует определенности, поэтому вещественные числа представляются в нормализованной форме.
Число с плавающей точкой является нормализованным, если:
1) наиболее значимая цифра в представлении f отлична от нуля:
1/b ≤ | f | < 1
2) f = 0 и е принимает наименьшее возможное значение
Например: 0.615, 0.101, 6.15, 0.01
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

p-разрядные нормализованные вещественные числа
( e, f ) = f ⋅ be-q
В ЭВМ для хранения вещественных чисел отводится ограниченное число разрядов:
–bp ≤ f ⋅ be-q ≤ bp
Пример: рассмотрим следующий пример представления десятичных чисел: f – 8-разрядов, е – 2 разряда, избыток q = 50, основание b = 10.
Число Авогадро: N = 6,02214⋅1023 = 0.602214⋅1024 =
((24+50),+.60221400) = (74, +.60221400)
Постоян. Планка: h = 6.6261 ⋅10-27 = 0.66261 ⋅10-26 =
((-26+50), +.66261000) = (24, +.66261000)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

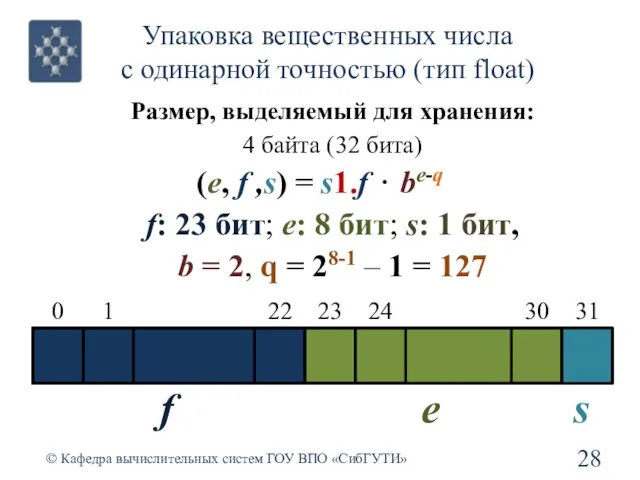
Упаковка вещественных числа
с одинарной точностью (тип float)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
0
Размер, выделяемый для хранения:
4 байта (32 бита)
(e, f ,s) = s1.f ⋅ be-q
f: 23 бит; e: 8 бит; s: 1 бит,
b = 2, q = 28-1 – 1 = 127
22
1
23
24
30
31
f
e
s

Примеры вещественных чисел
с одинарной точностью
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
( e, f ,s) = s1.f ⋅ be-q
( 127, 0 ,0) = +1.0 ⋅ 2127-127 = + 1.0

Примеры вещественных чисел
с одинарной точностью (2)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
( e, f ,s) = s1.f ⋅ be-q
( 127, 0 ,1) = –1.0 ⋅ 2127-127 = – 1.0

Примеры вещественных чисел
с одинарной точностью (3)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
( e, f ,s) = s1.f ⋅ be-q
( 126, 0 ,0) = +1.0 ⋅ 2126-127 = +0.5

Примеры вещественных чисел
с одинарной точностью (4)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
( e, f ,s) = s1.f ⋅ be-q
( 127, 0 ,0) = +1.0 ⋅ 2123-127 = +2-4 = 0.0625

Перевод вещественных чисел
из десятичной СС в двоичную СС
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Пусть дано десятичное вещественное число A10 = A'10 . A''10
Необходимо: найти A2
Решение:
Найти A'2 из A'10, используя алгоритм DB1 перевода целых десятичных чисел в двоичные.
Найти A''2 из A''10, используя алгоритм DB2 перевода дробных (<1) десятичных чисел в двоичные.
A2 = A'2.A''2

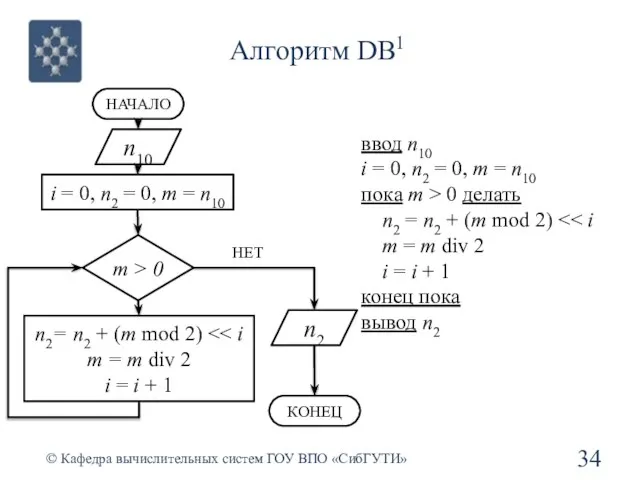
Алгоритм DB1
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
n10
i = 0, n2 = 0, m = n10
НАЧАЛО
m > 0
n2= n2 + (m mod 2) << i
m = m div 2
i = i + 1
КОНЕЦ
НЕТ
ввод n10
i = 0, n2 = 0, m = n10
пока m > 0 делать
n2 = n2 + (m mod 2) << i
m = m div 2
i = i + 1
конец пока
вывод n2
n2

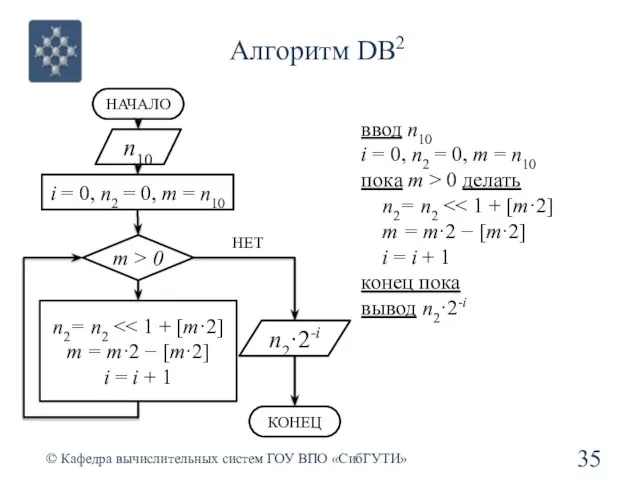
Алгоритм DB2
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
n10
i = 0, n2 = 0, m = n10
НАЧАЛО
m > 0
n2= n2 << 1 + [m·2]
m = m·2 − [m·2]
i = i + 1
КОНЕЦ
НЕТ
ввод n10
i = 0, n2 = 0, m = n10
пока m > 0 делать
n2= n2 << 1 + [m·2]
m = m·2 − [m·2]
i = i + 1
конец пока
вывод n2·2-i
n2·2-i

Представление числа 0.310
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
n10
i = 0, n2 = 0, m = n10
НАЧАЛО
m > 0
n2= n2 << 1 + [m·2]
m = m·2 − [m·2]
i = i + 1
КОНЕЦ
НЕТ
1. n2 = 02<<1 + [0.3·2] = 02
m = 0.6, i = 1
2. n2 = 0<<1 + [0.6·2] = 12
m = 1.2 – 1 = 0.2, i = 2
3. n2 = 12<<1 + [0.2·2] = 102
m = 0.4 – 0 = 0.4, i = 3
4. n2 = 102<<1 + [0.4·2] = 1002
m = 0.8 – 0 = 0.8, i = 4
5. n2 = 100<<1 + [0.8·2] = 10012
m = 1.6 – 1 = 0.6, i = 5
n2·2-5 = 0.01001
6. …
…
0.310 = 0.01001 1001 1001 1001 ….
n2·2-i

Примеры вещественных чисел
с одинарной точностью (5)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
( e, f ,s) = s1.f ⋅ be-q
( 127, 0 ,0) = +1.0011001… ⋅ 2125-127 =
1.0011001… ⋅ 2-2 = 0.010011001….

Примеры вещественных чисел
с одинарной точностью (6)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
( e, f ,s) = s1.f ⋅ be-q
( 127, 0 ,0) = +1.01010011001… ⋅ 2129-127 =
1.01010011001… ⋅ 22 = 101.010011001….

Анализ внутреннего представления
числа 5.310 в типе float
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
1.0101 0011 0011 0011 0011 0102 ⋅ 22 =
= 101.01 0011 0011 0011 0011 0102 =
5 + 2-2 + 2-5 + 2-6 + 2-9 + 2-10 +
2-13 + 2-14 + 2-17 + 2-18 + 2-20 =
5 + 0.25 + 0,03125 + 0,015625 +
+ 0,001953125 + 0,000976562 +
+ 0,00012207 + 0,000061035 +
+ 0,000007629 + 0,000003815 + 0,000000954 =
= 5,299999237 + 0,000000954 = 5,300000191

Примеры вещественных чисел
с одинарной точностью (7)
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
( e, f ,s) = s1.f ⋅ be-q
( 127, 0 ,0) = +1.010 0011 0011 … ⋅ 2129-127 =
1.010 0011 0011 … ⋅ 22 = 101.0 0011 0011 ….

Анализ внутреннего представления
числа 5.110 в типе float
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
1.010 0011 0011 0011 0011 00112 ⋅ 22 =
= 101.0 0011 0011 0011 0011 00112 =
5 + 2-4 + 2-5 + 2-8 + 2-9 +
2-12 + 2-13 + 2-16 + 2-17 + 2-20 + 2-21 =
5 + 0,0625 + 0,03125 +
0,00390625 + 0,001953125 +
+ 0,000244141 + 0,00012207 +
+ 0,000015259 + 0,000007629 +
0,000000954 + 0,000000477 = 5,099999905

Ошибки округления
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Технические средства не позволяют хранить числа, заданные бесконечными дробями
Необходима замена любого числа конечной дробью, ограниченной доступным количеством разрядов. Данная операция называется округлением.
Округлением числа x = ±dn…ds+1dsds–1ds–2 до s разрядов в заданной СС называется его замена числом xs = ±dn…ds+1ds, в котором разряды (s – 1), (s – 2), … являются нулевыми.
Разность (x – xs) называется ошибкой округления.

Способы округления
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Отбрасывание разрядов (s – 1), (s – 2),… как это реализовано для целых чисел. Достоинством данного подходя является простота реализации в аппаратуре. Недостатком служит то, что знак ошибки (x* − x) всегда противоположен знаку x.
Округление по правилам, используемым в школе. Вещественные числа Xis, имеющие нулевые младшие разряды
(s – 1), (s – 2), … располагаются на числовой оси с шагом bs, как показано на рисунке. При этом среди этих чисел есть число x*, которое наиболее близко к x и | x* − x | ≤ bs

Примеры применения алгоритмов округления для числа 5.310
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Отбрасывание разрядов:
5.3 = 101.01 0011 0011 0011 0011 0011 00112 =
5,299999237 + 2-21 = 5,299999714
5,299999714 − 5,3 = − 2.86 · 10-7
Округление с использованием школьной арифметики
5.3 = 101.01 0011 0011 0011 0011 00112 =
101.01 0011 0011 0011 0011 001 + 2-21 =
101.01 0011 0011 0011 0011 010 =
5,299999237 + 2-20 = 5,300000191
5,300000191 – 5,3 = 1.91 · 10-7

Примеры применения алгоритмов округления для числа 5.110
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Отбрасывание разрядов:
5.1 = 101.0 0011 0011 0011 0011 0011 00112 =
5,099999905
5,099999905 − 5,1 = − 0.95 · 10-7
Округление с использованием школьной арифметики
5.1 = 101.0 0011 0011 0011 0011 0011 00112 =
5,099999905
5,099999905 − 5,1 = − 0.95 · 10-7

Машинный ноль
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
( e, f ,s) = s1.f ⋅ be-q
( 0, 0 ,0) = +1.000 0000 0000 … ⋅ 20-127 =
1.000 0000 0000 … ⋅ 2-127 = 2-127

Машинный ноль
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Число ω, для которого f = 0, мантисса m = 1.0, а порядок e принимает наименьшее значение (для float e = 0 => (e – q)= – 127) называется машинным нулем.
Оно совпадает с минимальным положительным числом, которое может быть представлено числом с плавающей точкой при заданных размерностях f и e (для float размерность f – 23 бита, e – 8 бит).
Любое число x < ω рассматривается как 0.

Погрешности измерений
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Абсолютная погрешность (Δх) − разность между приближенным значением некоторой величины и ее точным значением: Δх = | xп – xт |, где xт – точное значение, а xп – приближенное.
Относительная погрешность (δx) – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины:
δx = Δх/xп,
δx = Δх/xт .
δx является безразмерной величиной

Погрешность представления
вещественных чисел
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
В отличие от чисел с фиксированной точкой, сетка чисел, которые способна отобразить арифметика с плавающей точкой, неравномерна: она более густая для чисел с малыми порядками и более редкая — для чисел с большими порядками.
Для чисел с фиксированной точкой постоянным является порядок абсолютной погрешности.
Для чисел с плавающей точкой постоянным является порядок относительной погрешности.

Погрешности вещественных чисел
с фиксированной точкой
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Рассмотрим 2-хразрядные числа с фиксированной точкой, один разряд отводится под целую часть, второй – под дробную.
x
…
0.1
0.2
0.3
1.0
1.1
1.2
…
0.123
1.123
Δх1 = | xп – xт | = | 0.123 – 0.1 | = 0.023, порядок 10-2.
Δх2 = | xп – xт | = | 1.123 – 1.1 | = 0.023, порядок 10-2.
δx1 = Δх/xп = 0.023/0.123 ≈ 0.186, порядок 10-1
δx2 = Δх/xп = 0.023/1.123 ≈ 0,020 , порядок 10-2

Погрешности вещественных чисел
с плавающей точкой
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Рассмотрим 2-хразрядные числа с плавающей точкой, один разряд отводится под мантиссу,
второй – под порядок.
x
…
0.1·10-9
0.2·10-9
0.3·10-9
0.3·109
0.123·10-9
0.123 ·109
Δх1 = | xп – xт | = 0.023·10-9, порядок 10-10.
Δх2 = | xп – xт | = 0.023·109, порядок 108.
δx1 = Δх/xп = 0.023·10-9 / 0.123·10-9 ≈ 0.186, порядок 10-1
δx2 = Δх/xп = 0.023·109 / 0.123·109 ≈ 0.186, порядок 10-1

Машинный эпсилон
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Машинным эпсилоном называется наименьшее положительное число ε такое, что
1 ⊕ ε ≠ 1,
где ⊕ − машинное сложение.
Пример:
Пусть даны два числа: a и b = a + γ.
Если γ < a·ε, то с точки зрения машины a = b.
a < a·(1 ⊕ γ) < a·(1 ⊕ ε)
1 ⊕ γ = 1

Программа поиска
машинного эпсилона
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
#include
int main()
{ float e,e1;
int k=0;
e=1.0;
do
{
e=e/2.0;
e1=e+1.0;
k++;
} while (e1>1.0);
printf("Число делений на 2: %d\n",k);
printf("Машинный эпсилон: %e\n",e);
return 0;
}
Результаты работы:
Число делений на 2: 24
Машинный эпсилон: 5.960464e-08

Алгоритм сложения чисел
с плавающей точкой
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Задача: найти число ω = υ ⊕ ν
а : (2p + 1) разрядный аккумулятор

Алгоритм нормализации чисел
с плавающей точкой
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Задача: обеспечить для числа ω = (eω , ± f ω), f ω < b
выполнение условия: 1/b ≤ | f ω | < 1
почему?

ИТОГИ
© Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»
Рассмотрены внутренние представления целых чисел:
целых чисел без знака
целых чисел со знаком
прямой код, обратный код, дополнительный код;
арифметические действия (сложение и вычитание) над знаковыми числами в дополнительном коде.
Внутреннее представление вещественных чисел:
вещественные числа с фиксированной и плавающей запятой;
упаковка вещественных чисел;
понятие машинного нуля, понятие погрешности вычислений, понятие машинного эпсилона;
арифметические действия (сложение и вычитание) над вещественными числами с плавающей точкой.