Содержание
- 2. Цели практики: 1) Закрепление и расширение теоретических и практических знаний по специальности и применение этих знания
- 3. Исследование нанотрубок имеет большие перспективы в развитии, так как они обладают уникальными комбинациями свойств. Такие свойства
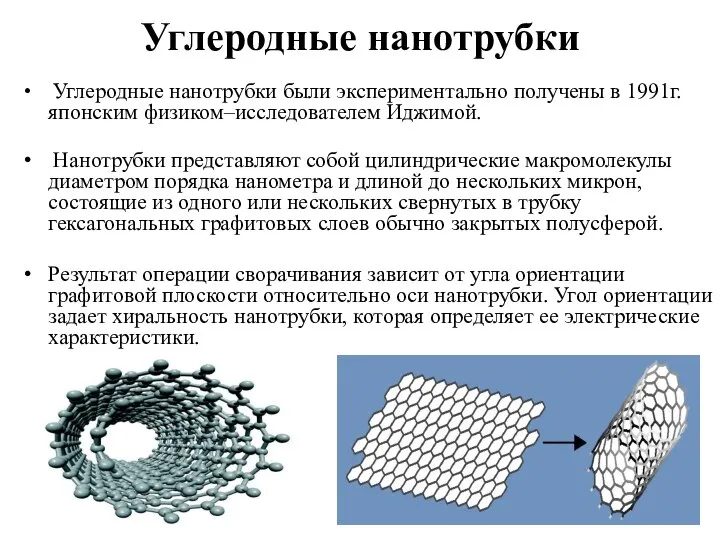
- 4. Углеродные нанотрубки Углеродные нанотрубки были экспериментально получены в 1991г. японским физиком–исследователем Иджимой. Нанотрубки представляют собой цилиндрические
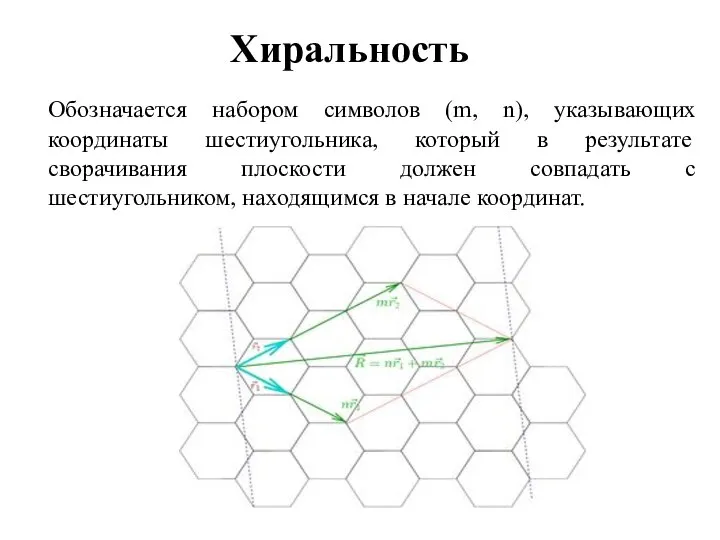
- 5. Хиральность Обозначается набором символов (m, n), указывающих координаты шестиугольника, который в результате сворачивания плоскости должен совпадать
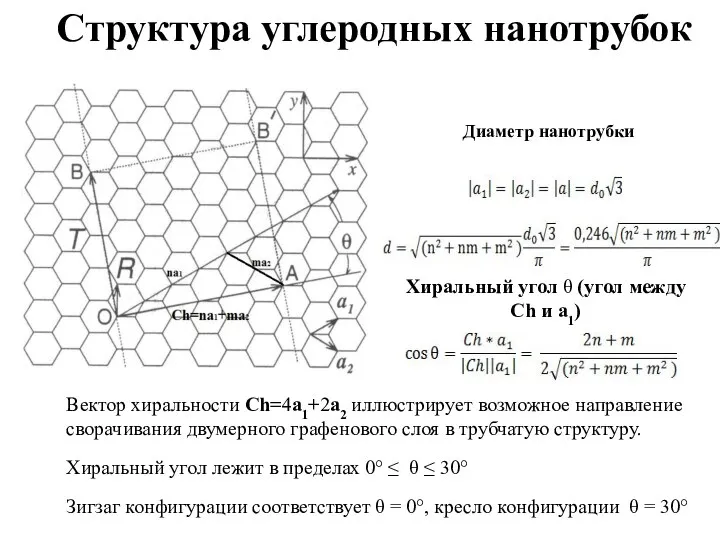
- 6. Структура углеродных нанотрубок Вектор хиральности Ch=4a1+2a2 иллюстрирует возможное направление сворачивания двумерного графенового слоя в трубчатую структуру.
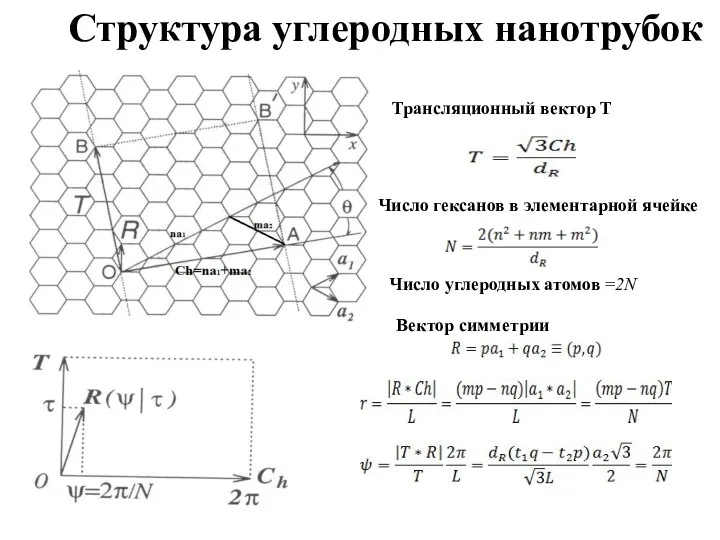
- 7. Трансляционный вектор T Структура углеродных нанотрубок Число гексанов в элементарной ячейке Число углеродных атомов =2N Вектор
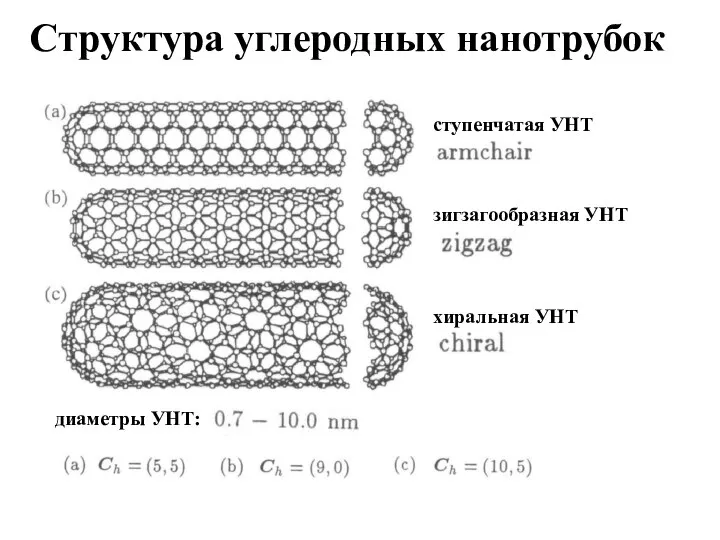
- 8. ступенчатая УНТ зигзагообразная УНТ хиральная УНТ диаметры УНТ: Структура углеродных нанотрубок
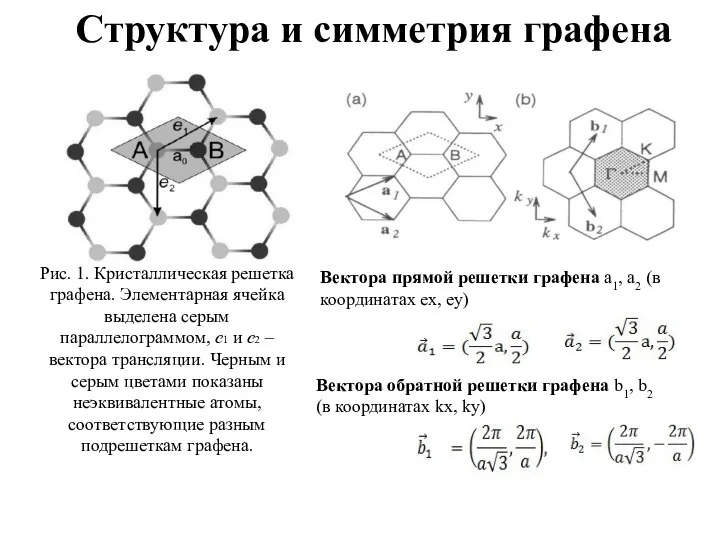
- 9. Структура и симметрия графена Вектора прямой решетки графена a1, a2 (в координатах ex, ey) Вектора обратной
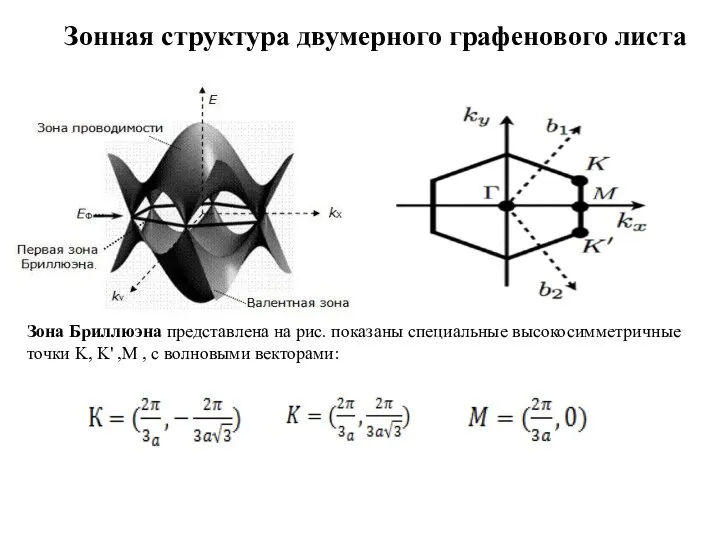
- 10. Зонная структура двумерного графенового листа Зона Бриллюэна представлена на рис. показаны специальные высокосимметричные точки K, K'
- 11. Линейный закон дисперсии Волновая функция графена представляется в виде блоховских функций отдельных электронов в различных подрешётках
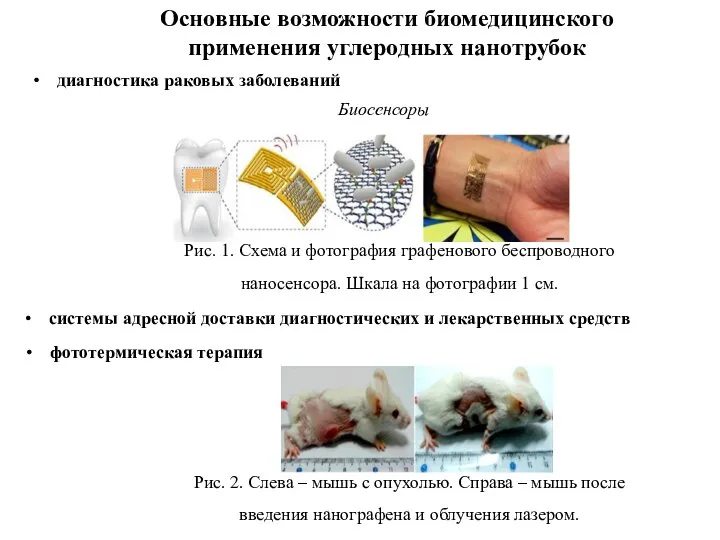
- 12. Основные возможности биомедицинского применения углеродных нанотрубок диагностика раковых заболеваний Биосенсоры Рис. 1. Схема и фотография графенового
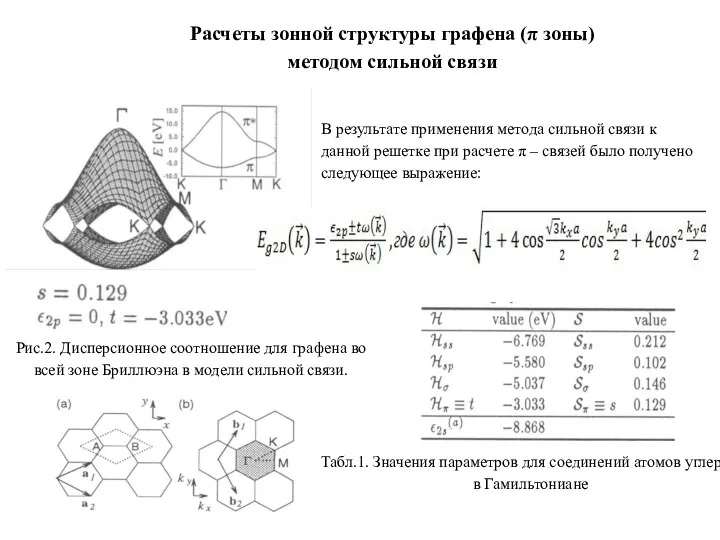
- 13. Рис.2. Дисперсионное соотношение для графена во всей зоне Бриллюэна в модели сильной связи. Расчеты зонной структуры
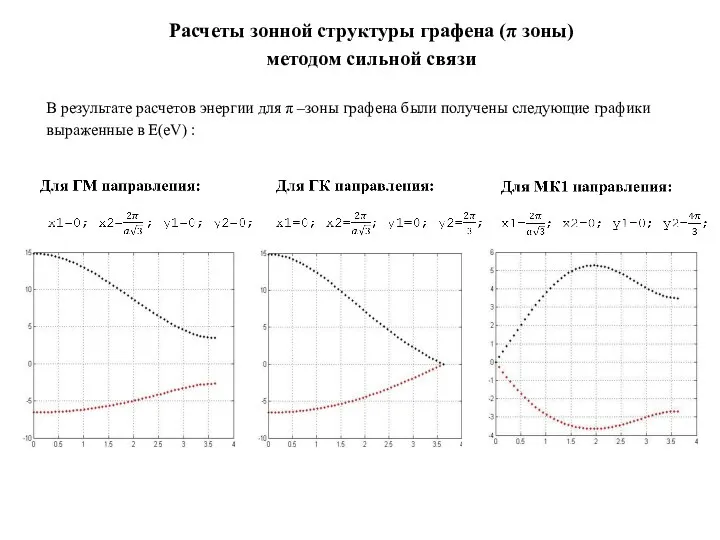
- 14. Расчеты зонной структуры графена (π зоны) методом сильной связи В результате расчетов энергии для π –зоны
- 16. Скачать презентацию



 Презентация на тему Цели, объекты и субъекты управления в таможенных органах
Презентация на тему Цели, объекты и субъекты управления в таможенных органах  Сжатие, архивация и разархивация данных. Архиваторы. Работа с архивами
Сжатие, архивация и разархивация данных. Архиваторы. Работа с архивами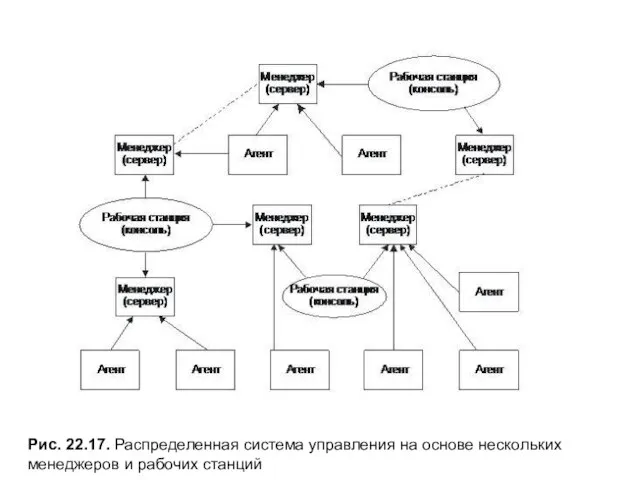 Рис. 22.17. Распределенная система управления на основе нескольких менеджеров и рабочих станций
Рис. 22.17. Распределенная система управления на основе нескольких менеджеров и рабочих станций Решение педагогических ситуаций как форма квалификационного испытания с целью подтверждения соответствия занимаемой должности
Решение педагогических ситуаций как форма квалификационного испытания с целью подтверждения соответствия занимаемой должности  Словари
Словари Ишемическая болезнь сердца
Ишемическая болезнь сердца  Выбор поставщика. Один или несколько?
Выбор поставщика. Один или несколько? Корпоративная система электронного документооборота
Корпоративная система электронного документооборота Презентация тренинга «Функции менеджера»
Презентация тренинга «Функции менеджера» Сварочная дуга
Сварочная дуга Организация государственной службы. Служебный контракт. Тема 32
Организация государственной службы. Служебный контракт. Тема 32 Форма волны
Форма волны Внеклассное занятияТема: «Сударыня Масленица»
Внеклассное занятияТема: «Сударыня Масленица»  Тема проектаГде живут витаминки?
Тема проектаГде живут витаминки? Т1 ГЗ 1 Инженерно-авиационная служба (ИАС)
Т1 ГЗ 1 Инженерно-авиационная служба (ИАС) HIOKI 3390
HIOKI 3390 Перелом
Перелом Музей-усадьба Льва Толстого
Музей-усадьба Льва Толстого Социальные коммуникации
Социальные коммуникации Социальная политика России в контексте сравнительной социальной политики
Социальная политика России в контексте сравнительной социальной политики Управление командой на основе Корпоративного портала.
Управление командой на основе Корпоративного портала. Опыт реализации инклюзивного образования в Норвегии
Опыт реализации инклюзивного образования в Норвегии Дробные числительные. 6 класс
Дробные числительные. 6 класс Социальная ипотекареальность и перспективыИнформация начальника МУ «Управление муниципального жилищного фонда и жилищной п
Социальная ипотекареальность и перспективыИнформация начальника МУ «Управление муниципального жилищного фонда и жилищной п ПРОЕКТ CВIТИЛЬНИК
ПРОЕКТ CВIТИЛЬНИК Презентация на тему Среднеазиатская черепаха
Презентация на тему Среднеазиатская черепаха Урок о дифференциации пола
Урок о дифференциации пола Презентация на тему Cтраны Северной Африки
Презентация на тему Cтраны Северной Африки