Слайд 3Среднее значение
Для небольшого набора n значений (для малой выборки) дискретной случайной

величины х1, х2, …, хn речь, строго говоря, идет лишь об оценках перечисленных измерителей риска.
Так, средним (ожидаемым) значением выборки, или выборочным аналогом математического ожидания, является величина
где - вероятность реализации значения случайной величины Х
Слайд 4Среднее значение
Если все значения равновероятны, то ожидаемое значение случайной выборки вычисляется

по формуле:
Слайд 5Ожидаемая доходность и риск портфеля
Принцип формирования портфеля, заключающийся в распределении средств

по различным видам активов в целях снижения рисков называется диверсификацией.
Любая экономическая проблема сводится к задаче наилучшего распределения ресурсов. Любой экономический субъект - отдельный человек, предприятие, либо правительство, сталкивается с вопросом – как распределить имеющиеся в его распоряжении ресурсы – материальные, финансовые, человеческие, и т.д. Экономическая теория исходит из того, что любой субъект, принимая решение, стремиться к наибольшей выгоде, то есть, действует рационально. Этот же принцип лежит в основе решений о наилучшем инвестировании.
Слайд 6 Что лучше для данного инвестора: держать свои сбережения под подушкой, разместить

их на банковском депозите, дать взаймы государству, купить акции предприятия А или В? Ответ на этот вопрос не очевиден.
Рассмотрим основные принципы так называемой современной портфельной теории (modern portfolio theory, MPT) – теории, которая пытается дать обоснованные ответы на поставленные вопросы. Начало современной портфельной теории было положено революционной работой Гарри Марковица в 1952 году. Результаты Марковица были развиты и дополнены не менее известными работами Джеймса Тобина, Вильяма Шарпа и других исследователей. Важность этих разработок для развития современной экономики и финансов подчеркивает Нобелевская премия по экономике, которой были удостоены перечисленные выше экономисты, в первую очередь, за развитие современной портфельной теории.
Слайд 8 Главным предположением, которое принял Гарри Марковиц, анализируя эту задачу, является то,

что для инвестора, при оценке альтернативных решений, важными являются только два параметра: первый ожидаемая доходность инвестиций
ожидаемая доходность (греческая буква «мю») равна математическому ожиданию доходности выбранных активов,
Слайд 9второй – стандартное отклонение доходности, как показатель, характеризующий риск принимаемого решения
Стандартное отклонение

(сигма) есть корень квадратный из дисперсии доходности ценных бумаг.
Другим, не менее важным предположением, является следующее: инвестор не обязательно должен выбрать какое-то одно решение, он может выбрать любую комбинацию возможных инвестиций, распределяя своё богатство по различным направлениям вложений.
Слайд 10Пусть ( i = 1, … n) – это доля от общего

объёма богатства, инвестируемого в i-й актив. Сформированную таким образом комбинацию инвестиций мы будем называть портфелем. Инвестору необходимо выбрать портфель, ожидаемая доходность и стандартное отклонение которого были бы для него наилучшими.
Прежде всего, необходимо установить какова средняя (ожидаемая) доходность портфеля ценных бумаг. Доходность портфеля определим как прирост богатства в расчёте на единицу вложений к моменту времени, рассматриваемому в качестве планового горизонта
Слайд 11где W – сегодняшний размер богатства, - размер богатства на конец периода.

Доходность портфеля можно рассчитать как взвешенную по объемам инвестиций доходность каждого входящего в портфель актива:
Ожидаемая доходность портфеля определяется по формуле математического ожидания суммы случайных величин:
=
Слайд 12Таким образом, ожидаемая доходность инвестиционного портфеля – это средневзвешенная по долям инвестиций

ожидаемая доходность каждого из активов, входящих в портфель.
Слайд 13Дисперсия доходности портфеля
Дисперсия доходности портфеля рассчитывается как дисперсия суммы случайных величин.

Напомним, что если и - случайные величины, то
где cov() – коэффициент ковариации случайных величин α и β.
Слайд 14Таким образом, для портфеля
тогда
Стандартное отклонение портфеля , тем самым, равно:

Слайд 15Диверсификация портфеля
Основной принцип работы на рынке ценных бумаг соответствует житейской мудрости:

«Никогда не клади все яйца в одну корзину». Применительно к рынку это означает, что инвестор не должен приобретать ценные бумаги только одного вида. Необходимо разнообразие, диверсификация вклада. В противном случае инвестор обрекает себя либо на низкую эффективность вклада, либо на излишне высокий риск.
Уменьшение риска за счет диверсификации портфеля приводит к снижению доходности портфеля. Риск, который не устраняется при помощи диверсификации, называется рыночным. Риск, который относится непосредственно к компании (эмитенту), называется диверсифицируемым или специфическим.
Слайд 16Модель Марковица
Модель поведения инвестора, согласно которой инвестиции оцениваются исключительно по двум

параметрам – ожидаемой доходности и риску, позволяет сформулировать единое правило формирования портфеля, которому следуют все без исключения инвесторы. Независимо от индивидуальных предпочтений, инвесторы стремятся сформировать эффективный портфель – такой, который обеспечивает минимальную степень риска для выбранного уровня дохода либо, что то же самое, максимальный ожидаемый доход при заданной степени риска. Этот подход и сама задача выбора эффективного портфеля носит название модели Марковица.
Слайд 17Суть диверсификации по Марковицу: для снижения риска портфеля необходимо распределить средства между

инвестициями, имеющими минимальную корреляцию. Соотношение риска и доходности – основа для принятия инвестором решения по формированию портфеля ценных бумаг. Модель Марковица можно сформулировать следующим образом: необходимо найти такие пропорции распределения средств между доступными активами: (где
- доля средств, инвестируемых в i-ый актив).
Слайд 18Математически модель можно сформулировать так. Найти
при ограничениях:

Слайд 19В приведённой формулировке модели, - заданный уровень средней доходности, а ковариация равна
В

модели Марковица допустимыми являются только стандартные портфели (без коротких позиций). Это значит, что на вектор Х накладываются два ограничения. Портфель называют стандартным, если инвестор по каждому активу находится в длинной (long) позиции. Длинная позиция - это обычно покупка актива с намерением его последующей продажи (закрытие позиций).
Слайд 20 Такая покупка обычно осуществляется при ожидании повышения цены актива в надежде

получить доход от разности цен покупки и продажи. Допустим, что относительно некоторого актива инвестор уверен, что грядет понижение его стоимости. В этом случае он может совершить сделку, которая называется короткой продажей (short sale). Для этого он берет данный актив взаймы у другого инвестора (кредитора), сразу же продает его, а впоследствии покупает на рынке по сниженной цене и возвращает его своему кредитору. При этом он обязан выплатить кредитору текущий доход по активу за время сделки и некоторый процент за предоставление самой возможности сделки (за кредит). На большинстве фондовых бирж короткие продажи вполне допустимы и часто используются, но ввиду их особой рискованности биржи могут вводить ограничения на общую величину коротких позиций в сделках.
Особенностью модели Марковица является то, что доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен.
Слайд 21
Модель Блека.
В модели Блека допустимыми являются любые портфели. Это значит, что

вектор Х удовлетворяет лишь основному ограничению:
Наличие коротких позиций (отсутствие условия неотрицательности) позволяет реализовать любую, сколь угодно большую доходность, естественно, за счет большого риска.
Слайд 22Модель Тобина-Шарпа-Литнера
В модели Тобина - Шарпа - Литнера предполагается наличие так

называемых безрисковых активов, доходность которых не зависит от состояния рынка и имеет постоянное значение.
Слайд 23Оценка эффективности управления портфелем
Доходность портфеля за определенный промежуток времени можно определить

как
Но эта формула не учитывает, что на протяжении рассматриваемого промежутка времени могли происходить как дополнительные вложения денежных средств, так и их изъятия. Для учета этого факта при расчете используют два подхода - метод взвешенной по стоимости доходности и метод взвешенной по времени доходности.
Слайд 24Взвешенная по стоимости доходность портфеля (в годовом измерении) определяется как решение относительно

r уравнения:
где - средства, дополнительно вносимые в момент времени t (величина - с отрицательным знаком означает изъятие), а t – соответствующий промежуток времени от начала периода.
Слайд 25Оценка эффективности управления портфелем
Взвешенная по времени доходность определяется как средняя величина

доходности за каждый промежуток времени между моментами внесения и изъятия средств, то есть доходность за оцениваемый промежуток времени равна:
Слайд 26
Показатели эффективности:
1) Наиболее простым показателем эффективности управления портфелем является средняя доходность

за определенный исторический период. Средняя доходность определяется как:
Слайд 28Показатели эффективности:
Величина
называется коэффициентом Шарпа. Коэффициент Шарпа – один из наиболее простых,

но в то же время эффективных показателей эффективности управления портфелем. Он показывает степень устойчивости превышения оцениваемым портфелем безрисковой ставки доходности.
Слайд 31VAR - «стоимость под риском» (value at risk)
Рыночный риск – это

возможность несоответствия характеристик экономического состояния объекта значениям, ожидаемым лицами, принимающими решения под действием рыночных факторов.
Риски, связанные с инвестициями в ценные бумаги, – это, прежде всего:
кредитный риск, который по отношению к облигации состоит в том, что фактические доходы по этим инструментам могут не совпадать с теми, которые декларированы условиями выпуска. Например, в случае неплатёжеспособности эмитента, обладатель облигации может рассчитывать на некоторые выплаты (когда облигация обеспечена, например, имуществом эмитента), но они могут отличаться от обещанных как по размеру, так и по срокам;
Слайд 32риск досрочного выкупа, так как неопределённость выплат может быть заложена в самих

условиях выпуска облигаций, например, эмитент может зарезервировать за собой право досрочного выкупа по заранее определённой стоимости, если рыночные ставки доходности изменились неблагоприятным образом;
процентный риск есть отражение системного (рыночного) риска. Это риск изменения доходности (процентных ставок) на рынке в целом. Если кредитный риск (риск невыполнения обязательств) различается для различных видов облигаций, то процентный риск одинаков для всех их разновидностей;
инфляционный риск – риск непредвиденных изменений темпов инфляции.
Слайд 33 Рассмотренные ранее традиционные меры риска, к сожалению, обладают следующими серьезными недостатками:
Многие

из них не могут быть агрегированы, так, например, нельзя агрегировать дельта- и вега-риски. Факторы риска не могут быть агрегированы для различных рынков.
Традиционные меры риска не измеряют «капитал под риском», т.е. капитал, покрывающий потери, вызываемые данными факторами риска. Поэтому на основе этих показателей трудно анализировать качество управления портфелем с учетом риска.
Традиционные меры риска сравнительно плохо позволяют контролировать риск. Лимиты позиций, определяемые по факторам риска или показателям чувствительности, часто неэффективны.
Слайд 34 Все это объясняет ту огромную популярность, которой в современном риск-менеджменте пользуется

подход к измерению рисков на основе показателя «стоимость под риском» (value at risk - VAR).
VAR – это выраженная в данных денежных единицах (базовой валюте) оценка величины, которую не превысят ожидаемые в течение данного периода времени потери с заданной вероятностью.
Показатель VAR обычно не используется применительно к рынкам, находящимся в состоянии кризиса.
Слайд 35 Пусть фиксирован некоторый портфель открытых позиций. VAR портфеля для данного доверительного

уровня (1- ) и данного периода поддержания позиций t определяется как такое значение, которое обеспечивает покрытие возможных потерь «х» держателя портфеля за время t с вероятностью (1- ):
Слайд 36 Как следует из определения, величина VAR для портфеля заданной структуры –

это наибольший ожидаемый убыток, обусловленный колебаниями цен на финансовых рынках, который рассчитывается:
на определенный период времени в будущем (временной горизонт);
с заданной вероятностью его непревышения (уровень доверия);
при данных предположениях о характере поведения рынка.
Слайд 37 Доверительный интервал и временной горизонт являются ключевыми параметрами, без которых невозможны

ни расчет, ни интерпретация показателя VAR. Так, значение VAR в 10 млн. руб. для временного горизонта в один день и доверительного интервала 99% будет означать (при условии сохранения тенденций рыночной конъюнктуры):
вероятность того, что в течение следующих 24 часов мы потеряем меньше, чем 10 млн. руб., составляет 99%;
вероятность того, что наши убытки превысят 10 млн. руб. в течение ближайших суток, равна 1%;
убытки, превышающие 10 млн. руб., ожидаются в среднем один раз в 100 дней торгов.




































 Обеспечение непрерывного IT-образования в школе и вузе в условиях перехода на образовательные стандарты нового поколения
Обеспечение непрерывного IT-образования в школе и вузе в условиях перехода на образовательные стандарты нового поколения РОЛЬ СПЕЦИАЛЬНЫХ ЗНАНИЙ В ОБЛАСТИ ПСИХИАТРИИ И ПСИХОЛОГИИ В РАЗВИТИИ ЮВЕНАЛЬНОЙ ЮСТИЦИИ Е.И. Цымбал
РОЛЬ СПЕЦИАЛЬНЫХ ЗНАНИЙ В ОБЛАСТИ ПСИХИАТРИИ И ПСИХОЛОГИИ В РАЗВИТИИ ЮВЕНАЛЬНОЙ ЮСТИЦИИ Е.И. Цымбал Процессоры ADSP-BF53
Процессоры ADSP-BF53 Жизнь и творчество Виктора Михайловича Васнецова
Жизнь и творчество Виктора Михайловича Васнецова Все о полиграфическом рынке
Все о полиграфическом рынке История Голливуда и независимого кино
История Голливуда и независимого кино Зачем людям имена
Зачем людям имена ООО «ФЛЭР ИНЖИНИРИНГ»
ООО «ФЛЭР ИНЖИНИРИНГ» Презентация отряда имени В.Куриленко
Презентация отряда имени В.Куриленко Презентация на тему Мамин Сибиряк
Презентация на тему Мамин Сибиряк Проблемы и возможности борьбы с фальсифицированными продуктами/скрининг лекарственных средств
Проблемы и возможности борьбы с фальсифицированными продуктами/скрининг лекарственных средств Гипертекстовая интерпретация отрывка из оды М.В. Ломоносова
Гипертекстовая интерпретация отрывка из оды М.В. Ломоносова Colección de Barbies
Colección de Barbies Искусство Гжели
Искусство Гжели Презентация на тему Эрнест Резерфорд
Презентация на тему Эрнест Резерфорд Презентация на тему Польша
Презентация на тему Польша Автобус Wubbo Superbus (ОАЭ)
Автобус Wubbo Superbus (ОАЭ) Презентация на тему Скульптура Древнего Рима
Презентация на тему Скульптура Древнего Рима 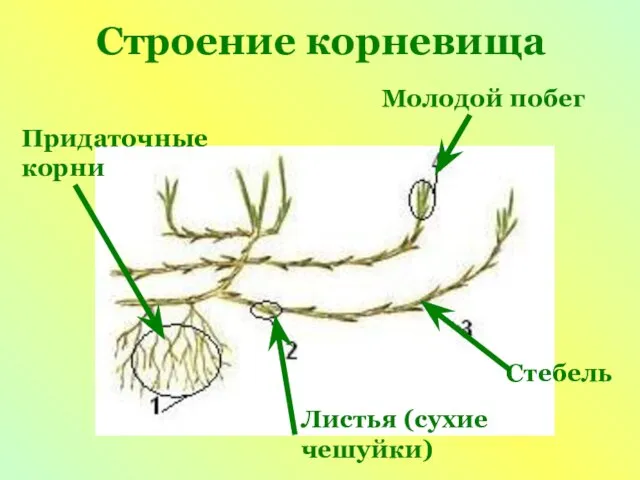 Видоизмененные побеги
Видоизмененные побеги ПОДБОР ВЫСОКОКВАЛИФИЦИРОВАННОГО ПЕРСОНАЛА
ПОДБОР ВЫСОКОКВАЛИФИЦИРОВАННОГО ПЕРСОНАЛА Презентация на тему Биотопы суши
Презентация на тему Биотопы суши Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники БИЗНЕС: ПОИСК ИДЕИ
БИЗНЕС: ПОИСК ИДЕИ Die Muscheln
Die Muscheln Актуализация грамматического материала при интенсивной подготовке к ГИА
Актуализация грамматического материала при интенсивной подготовке к ГИА Логика
Логика УСТРОЙСТВО РИМСКОЙ РЕСПУБЛИКИ
УСТРОЙСТВО РИМСКОЙ РЕСПУБЛИКИ Организация производственного процесса
Организация производственного процесса