Ох, уж эта математика!

Сегодня ты пришёл вот в этот класс,
Не вспоминать недобрым этот час,
Чтоб посидеть, подумать, отдохнуть,
На всё вокруг обдуманно взглянуть.
Пусть ты не станешь Пифагором,
Каким хотел бы, может, быть,
Но будешь ты рабочим, а может, и учёным
И будешь математику любить.

Условия проведения игры:
Игра состоит из 7 конкурсов + конкурс для болельщиков;
Каждый конкурс оценивается в баллах;
Команда, набравшая большее количество баллов, считается победительницей.

Кто
первый?

Разминка для 1команды

Выбери верные утверждения:
Площадь параллелограмма равна:
произведению его сторон;
произведению его высот;
произведению его стороны на высоту, проведенную к данной стороне.

Площадь квадрата со стороной 3 см равна:
6 см²;
8 см;
9 см².

Закончите предложение: «Площадь ромба равна…
произведению его сторон»
половине произведения его диагоналей»
произведению его стороны и высоты»

По формуле можно вычислить:
площадь треугольника;
площадь прямоугольника;
площадь параллелограмма

Площадь трапеции АВСД с основаниями АВ и СД и высотой ВО вычисляется по формуле:

Теорема Пифагора утверждает, что в прямоугольном треугольнике:
квадрат гипотенузы равен квадрату катета;
квадрат гипотенузы равен сумме квадратов катетов;
сумма квадратов катетов равна гипотенузе.

Разминка для 2 команды

Площадь квадрата равна:
произведению его сторон;
квадрату его стороны;
произведению его сторон на высоту

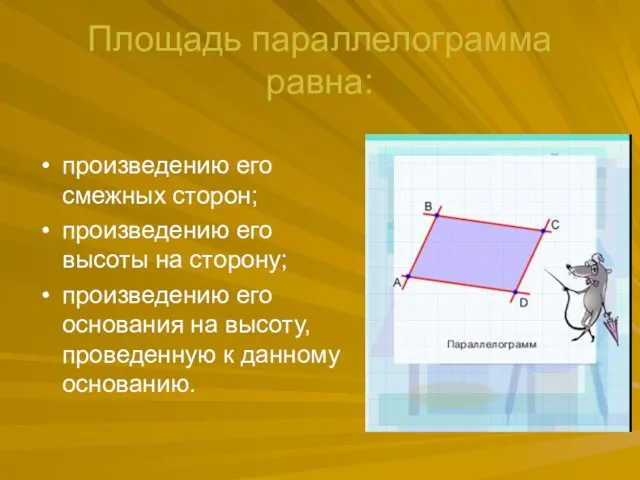
Площадь параллелограмма равна:
произведению его смежных сторон;
произведению его высоты на сторону;
произведению его основания на высоту, проведенную к данному основанию.

По формуле S=d*d /2 можно вычислить площадь:
ромба;
треугольника;
параллелограмма.

Площадь треугольника равна половине произведения:
оснований;
основания на высоту, проведенную к данному основанию;
его высот.

Площадь трапеции АВСД с основаниями ВС и АД и высотой ВН равна
S=(AB+CD)/2*BH;
S=(AD+BC)/2/BH;
S=(BC+AD)/2*BH.

Теорема Пифагора утверждает, что в прямоугольном треугольнике:
квадрат катета равен квадрату гипотенузы;
квадрат гипотенузы равен сумме квадратов катетов;
сумма квадратов катетов равна гипотенузе.

Мозг, хорошо устроенный, стоит больше,
чем мозг , хорошо наполненный.
М.Монтень

Найди
лишнее...

Перед вами четырехугольники.
1 2 3 4
Какой из четырехугольников по очень важному признаку является лишним?
Какая из фигур обладает наибольшим количеством свойств?
Для какого четырехугольника имеет смысл выражение: «Найти среднюю линию»?
Название какой фигуры в переводе с греческого языка означает «обеденный столик»?

Что ты знаешь
обо мне?

Квартирный
вопрос

Задача
Сколько трубок обоев пойдет на ремонт кабинета размером 6*8*3м, если в кабинете имеется 3 окна шириной по 2 метра каждое.

Прайс-лист
Расход материалов:
1 пачка клея на 6 трубок обоев,
1 бордюр на 4 трубки обоев.

Минута на
размышление

Командам предлагается решить задачи по готовым чертежам. Каждая задача стоимостью 2 балла. Отвечает та команда первой ,которая первой поднимет сигнальную карточку.
! Если другая команда предлагает иной правильный способ решения задачи, то она получает 2 балла.!

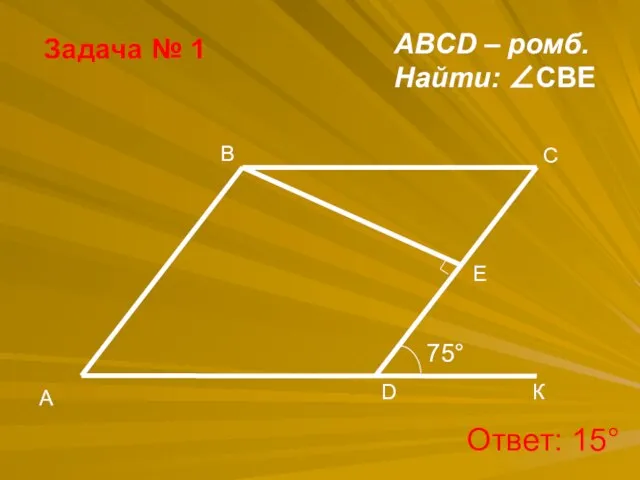
Задача № 1
ABCD – ромб.
Найти: ∠CBE
Ответ: 15°

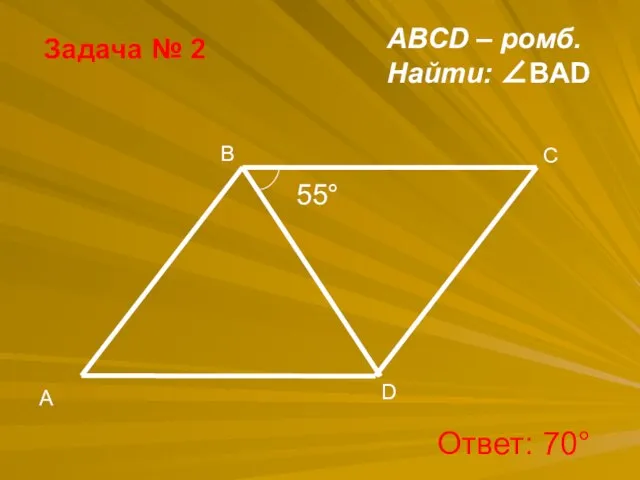
Задача № 2
ABCD – ромб.
Найти: ∠BAD
Ответ: 70°

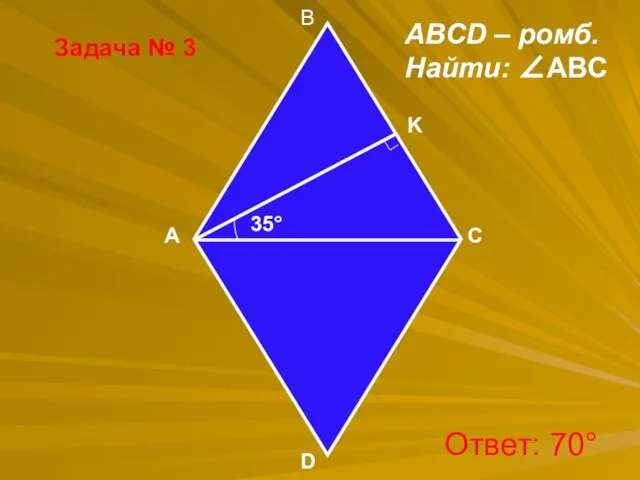
Задача № 3
B
A
D
C
∟
ABCD – ромб.
Найти: ∠ABC
K
35°
Ответ: 70°

Чёрный ящик
?

Одним – двумя высказываниями характеризуется предмет(его свойства, история возникновения и т.д.), который надо отгадать. Если предмет отгадан, то команда зарабатывает максимальное количество баллов, иначе даётся подсказка, которая снижает стоимость ответа и т.д.

Этот предмет – источник множества задач по математике, логике, комбинаторике, программированию (10 очков)
Родина – государство Лидия. Предположительно 7 век до н. э. (9 очков)
На Руси появились в 10 веке (8 очков)
На нем имеется специальное изображение (7 очков)
С названием этого предмета связано название известного российского двора (5 очков)
Бывает золотым, серебряным, медным (4 очка)
Этот предмет получил Буратино от папы Карло (2 очка)

Открытие датируется 1839 годом (10 очков)
Получение этого предмета связано с процессами дагерротипией и калотипией (9 очков)
Некоторые приложения Windows предназначены для работы с этим предметом (8 очков)
Получают его с помощью предмета, который изобрели Ньепс и Дагер (Франция) (7 очков)
Бывает черно-белым и цветным (5 очка)
Связан с фирмами Кодак, Коника и другими (4 очка)
Имеется в паспорте (2 очка)

С геометрией
на "ты"

1 команда
Диагонали ромба
12 см и 16 см Найти сторону ромба
В треугольнике АВС, <С = 90°, СВ = 5 см, АВ = 13 см. Найти площадь треугольника.
2 команда
Стороны прямоугольника 5 см и 12 см. Найти диагональ прямоугольника.
В ∆ABC <С = 90°, АВ = 5 см, АС = 3 см. Найти площадь треугольника.

1 команда
В прямоугольной трапеции основания равны 17 см и 5 см, а большая боковая сторона 13 см. Найти площадь трапеции.
2 команда
В прямоугольной трапеции боковые стороны равны 15 см и 9 см, а большее основание 20 см. Найти площадь трапеции.

Пифагор
Великий древнегреческий математик

По преданию Пифагор родился около 580 г. до нашей эры на острове Самос. Первые познания он мог получить от своего отца, ювелира: в те времена эта профессия требовала многосторонней образованности. Для тогдашней греческой молодежи посещение чужих стран было главным способом расширить запас знаний, и поэтому юность свою Пифагор провел в путешествиях.
Ему было лет тридцать, когда он приехал в Египет и там познакомился с древней мудростью жрецов: медициной, математикой и метеорологией. Говорят, что при вторжении персов в Египет, Пифагор был захвачен в плен и отвезен в Вавилон. Существует легенда, будто в то время он встретился с иранским пророком Заратустрой и даже побывал в Индии. Но, по мнению большинства историков, эти сведения являются скорее романом, чем историей.

Для своих современников Пифагор, прежде всего, был религиозным пророком, воплощением высшей божественной мудрости. О Пифагоре ходило много сказок, вроде тех, что у него было золотое бедро, что люди видели его в одно и то же время в разных местах. В некоторых текстах он предстает как полубог, тем, кем сам он себя воображал – сыном Гермеса. Пифагор считал, что существует три типа существ – боги, простые смертные и ... «похожие на Пифагора». В литературе пифагорейцы чаще всего изображались суеверными и весьма разборчивыми вегетарианцами, но совсем не математиками. Так кем же был на самом деле Пифагор: математиком, философом, пророком, святым или шарлатаном?

Пифагор создал свою философскую школу в Кротоне. Он выступает с проповедью нравственного совершенствования и познания, за что жители избрали его цензором нравов, духовным отцом города. Большое внимание Пифагор уделял исследованиям математических отношений, заложил основы теории пропорций.

Он смог доказать теорему, названную его именем, пользуясь геометрическим методом, единственным приемлемым для того времени. Пифагор умер в Метапонте (Южная Италия) около 500 года до н.э., куда он бежал после восстания в Кротоне. Его ученики обосновались в разных городах Великой Греции и организовали там пифагорейские общества.

Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
c
a
b

Пифагоровы штаны
Шуточное название теоремы Пифагора, возникшее в силу того, что раньше в школьных учебниках эта теорема доказывалась через доказательство равенства суммы площадей квадратов, построенных на катетах прямоугольного треугольника, площади квадрата, построенного на гипотенузе этого треугольника. Построенные на сторонах треугольника и расходящиеся в разные стороны квадраты напоминали школьникам покрой мужских штанов, что породило следующее стихотворение: «Пифагоровы штаны — на все стороны равны».

Слово жюри