Слайд 2 Цели:
установить связи между графиками функций вида у=ах2 , у=ах2+m, у=а(х+n)2;
обобщить выводы

для функции вида у=а(х+n)2+m.
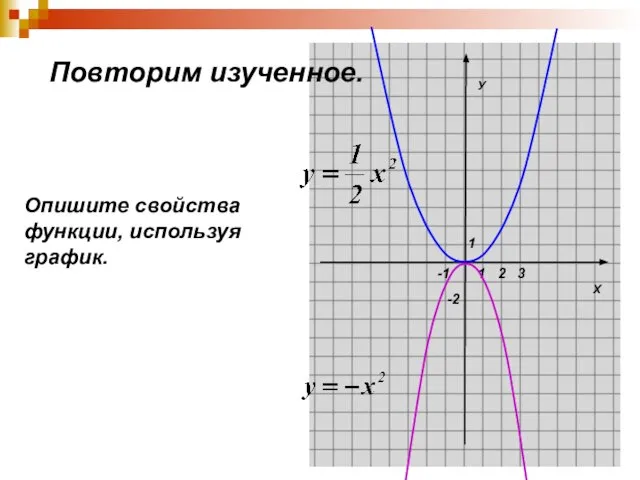
Слайд 3Х
У
1
1
-2
2
3
-1
Опишите свойства
функции, используя
график.
Повторим изученное.
Слайд 51) Построим график квадратичной функции вида
у=ах2+m
0,5
-2
-3,5
-4
-3,5
-2
0,5
Сравните с графиком
исходной функции
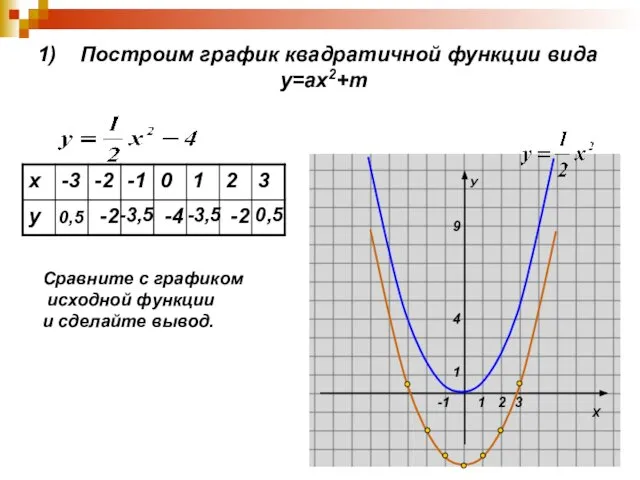
и сделайте вывод.
Слайд 6 График функции у=ах2+m может быть получен из графика функции у=ах2 путем

переноса его вдоль оси Оу на m единиц…
Слайд 72) Построим график квадратичной функции вида
у=а(х+n)2
0
0,5
2
4,5
0,5
2
4,5
Сравните с графиком
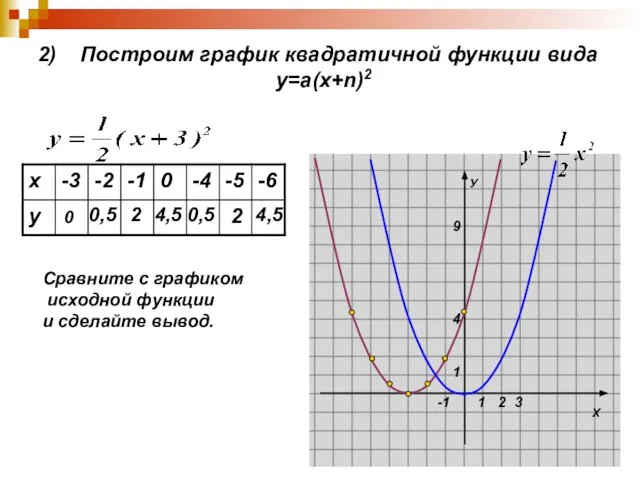
исходной функции
и сделайте вывод.
Слайд 8 График функции у=а(х+n)2 может быть получен из графика функции у=ах2 путем

переноса его вдоль оси Ох на n единиц…
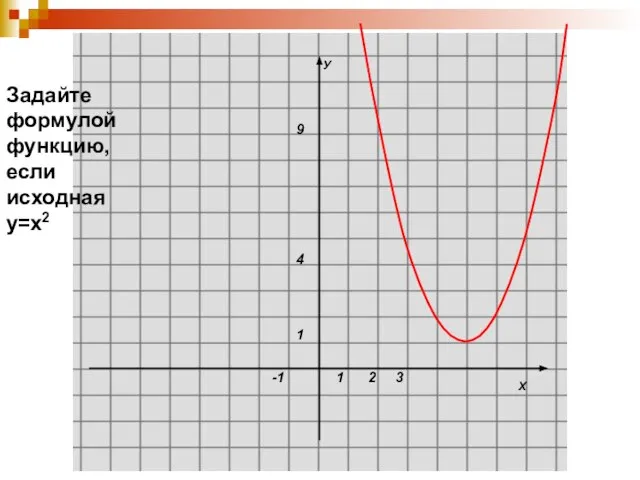
Слайд 9Задайте
формулой
функцию,
если
исходная
у=х2
Слайд 10 График функции у=а(х+n)2+m может быть получен из графика функции у=ах2 путем

переноса его вдоль оси Оу на m единиц… и вдоль оси Ох на n единиц…
Слайд 11У
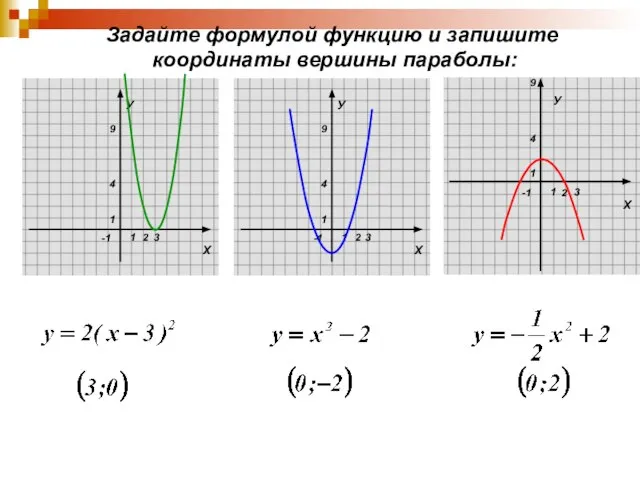
Задайте формулой функцию и запишите
координаты вершины параболы:
Слайд 12У
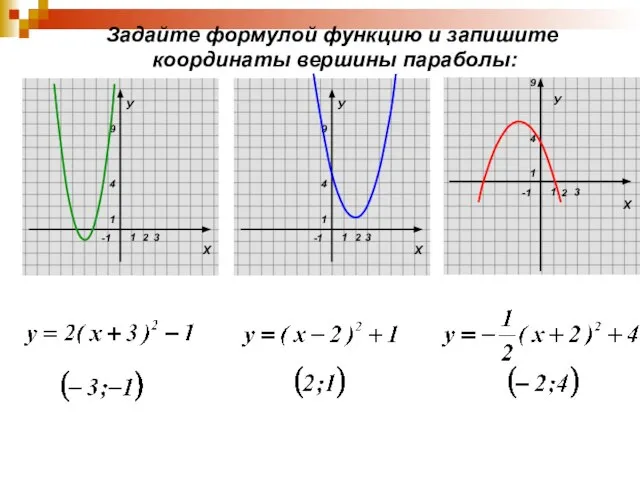
Задайте формулой функцию и запишите
координаты вершины параболы:
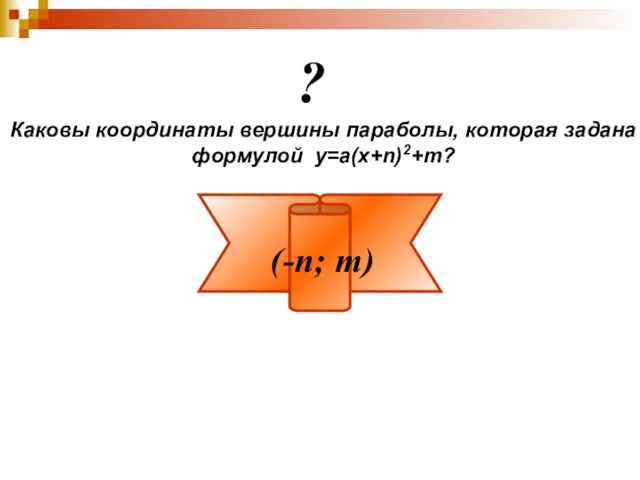
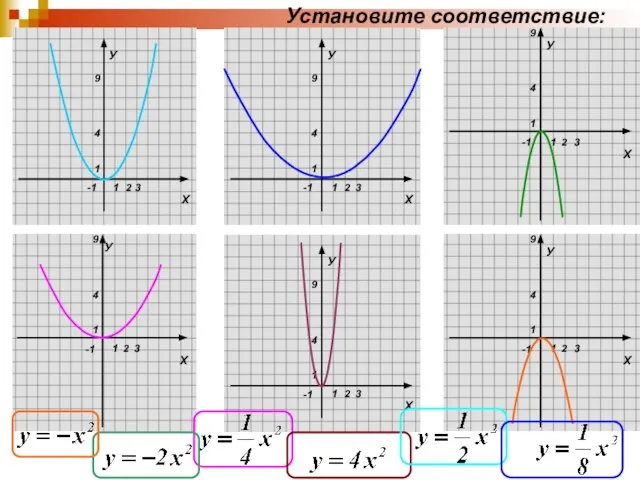
Слайд 13Каковы координаты вершины параболы, которая задана
формулой у=а(х+n)2+m?
?
(-n; m)











 Федеральное государственное автономное образовательное учреждение дополнительного профессионального образования«Академия по
Федеральное государственное автономное образовательное учреждение дополнительного профессионального образования«Академия по Обработка нижнего среза изделия
Обработка нижнего среза изделия Do you know Great Britain?
Do you know Great Britain? Интегральные микросхемы. Лекция 3
Интегральные микросхемы. Лекция 3 Огневая подготовка
Огневая подготовка Характеристика фашистских режимов в европе
Характеристика фашистских режимов в европе Рисуем зимний пейзаж
Рисуем зимний пейзаж тест
тест Настоящая презентация подготовлена неправительственной организацией Лига офицеров Севастополя и не является отражением официа
Настоящая презентация подготовлена неправительственной организацией Лига офицеров Севастополя и не является отражением официа Weather
Weather VPR_v_VS_T_17_Z_1
VPR_v_VS_T_17_Z_1 Spheres of employment
Spheres of employment Монастырь
Монастырь Английские социал-демократические рабочие партии
Английские социал-демократические рабочие партии Презентация на тему ГИДРОСФЕРА ЗЕМЛИ
Презентация на тему ГИДРОСФЕРА ЗЕМЛИ  Виктор Петрович Астафьев Жизнь и творчество
Виктор Петрович Астафьев Жизнь и творчество Стратегия игр
Стратегия игр Функции выборов и типологии избирательных систем
Функции выборов и типологии избирательных систем Школа и семья: От сосуществования к партнёрству
Школа и семья: От сосуществования к партнёрству БАСКЕТБОЛ
БАСКЕТБОЛ Презентация на тему История тепловых двигателей
Презентация на тему История тепловых двигателей  Международный день без интернета
Международный день без интернета Калибраторы. Назначение калибратора
Калибраторы. Назначение калибратора Тьюторский семинар
Тьюторский семинар Как повысить эффективность командной работы? Внутренний портал компании
Как повысить эффективность командной работы? Внутренний портал компании Европейское кафе с авторской кухней
Европейское кафе с авторской кухней Дошкольное воспитание
Дошкольное воспитание ТЕМА: «СОБРАНИЕ И КОНФЕРЕНЦИЯ ГРАЖДАН»ЧАСТЬ - 1 АНАЛИЗ НПА
ТЕМА: «СОБРАНИЕ И КОНФЕРЕНЦИЯ ГРАЖДАН»ЧАСТЬ - 1 АНАЛИЗ НПА