Планирование маршрута доставки груза в смешанном сообщении

В общих чертах
Предметом транспортной логистики является комплекс задач планирования и управления, связанных с перемещением грузов.
Сравнительный анализ «плохого» и «хорошего» вариантов свидетельствуют, что формирование маршрутов должно строиться на известных принципах:

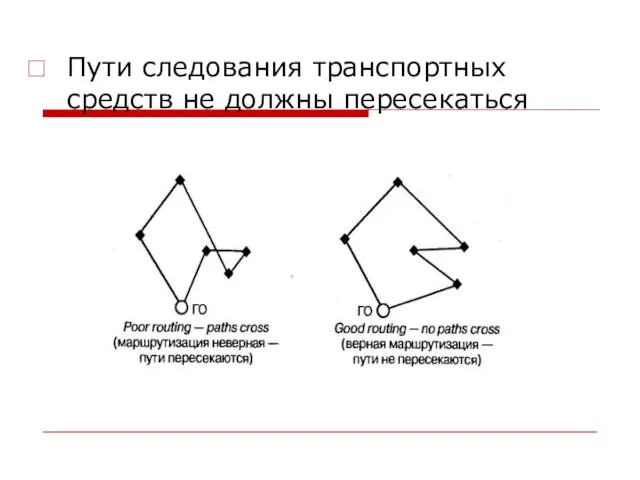
Пути следования транспортных средств не должны пересекаться

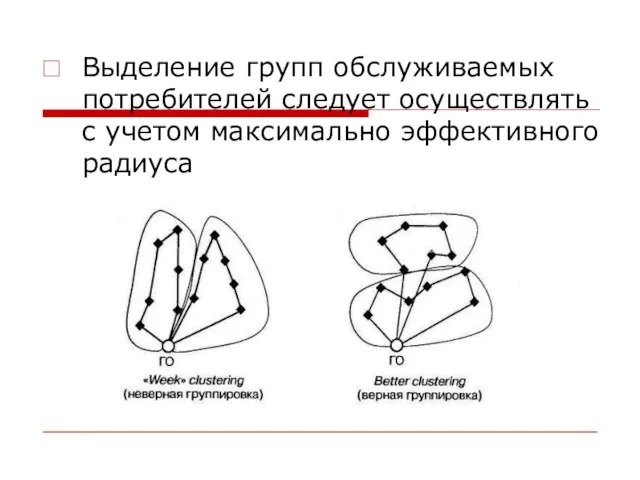
Выделение групп обслуживаемых потребителей следует осуществлять с учетом максимально эффективного радиуса

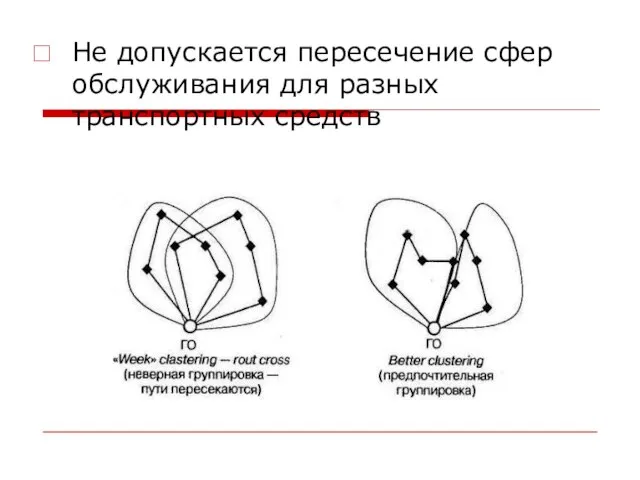
Не допускается пересечение сфер обслуживания для разных транспортных средств

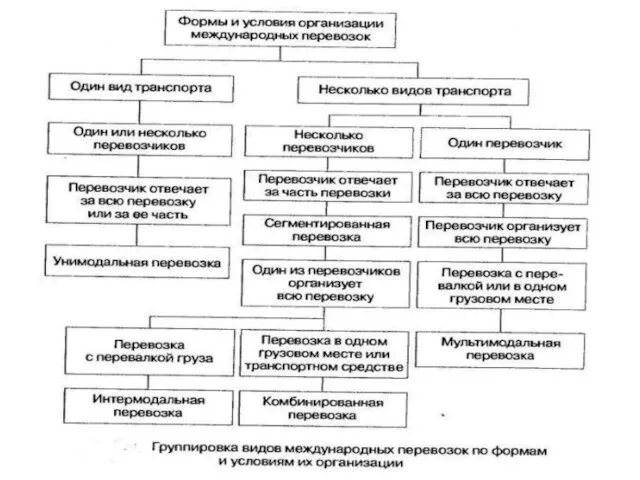
Смешанная перевозка
это транспортировка грузовой партии от пункта отправления до пункта назначения, когда в процессе перемещения используется более одного вида транспорта.
Посредством такой системы доставки выполняются условия «точно в срок» и «от двери до двери».

А теперь о главном.
Для планирования смешанной перевозки грузов наиболее актуальной является использование сетевых моделей.
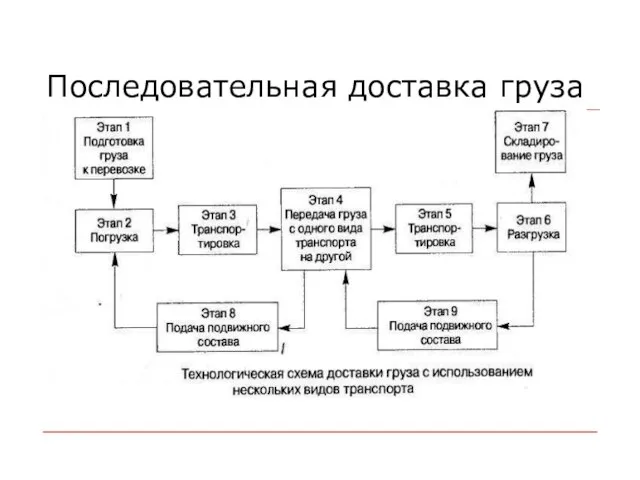
Основным материалом для сетевого планирования является структурная таблица комплекса работ, содержащая:
Перечень элементарных работ комплекса
Перечень работ, на которые опираются элементарные работы
Время выполнения каждой работы

Работы – вектора (дуги). Их проекции на ось времени равны времени их выполнения.
Моменты завершения работ – это узлы графика.

Vi - исходное событие (критический путь)
E(Vi) – ранние сроки события.
Пусть в iое событие входит несколько работ с номерами k,p,…,z.
Из всех сумм E(Vk)+tki, E(Vp)+tpi,…,E(Vz)+tzi,
E(Vi)=max из найденных значений.
L(Vi) – поздний срок наступления события.
L(Vn)= E(Vi) для последней работы n.
Из всех разностей L(Vk)+tik, L(Vp)+tip,…,L(Vz)+tiz,
L(Vi)=min из найденных значений.

Vi - исходное событие (некритический путь)
Rij = L(Vi)-E(Vi) – общий резерв. rij = E(Vj)-E(Vi)- tij – свободный резерв.
Pij = E(Vj)-L(Vi)- tij – независимый резерв

Последовательная доставка груза

Критерии выбора вариантов доставки:
Время (T)
Стоимость (C)
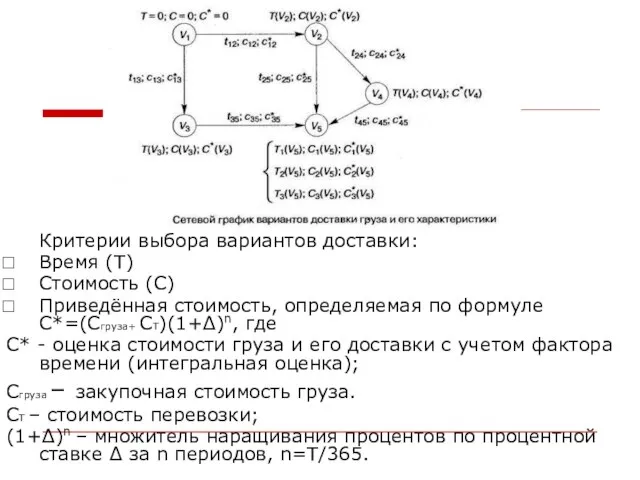
Приведённая стоимость, определяемая по формуле C*=(Cгруза+ CT)(1+Δ)n, где
С* - оценка стоимости груза и его доставки с учетом фактора времени (интегральная оценка);
Cгруза – закупочная стоимость груза.
CT – стоимость перевозки;
(1+Δ)n – множитель наращивания процентов по процентной ставке Δ за n периодов, n=T/365.

Критерии принятия решения в условиях неопределённости

Пример.
Необходимо осуществить перевозку 20футового контейнера из порта Хельсинки до центрального склада в Москве.

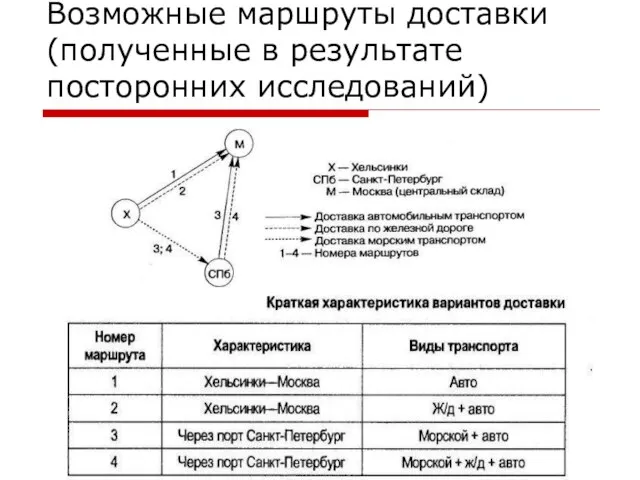
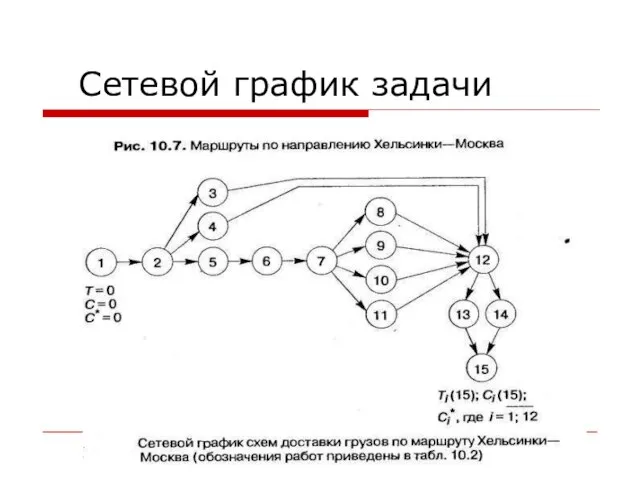
Возможные маршруты доставки (полученные в результате посторонних исследований)

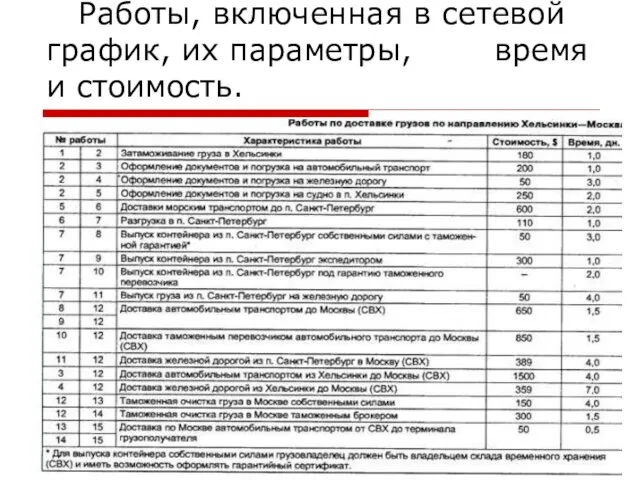
Сетевой график задачи

Работы, включенная в сетевой график, их параметры, время и стоимость.

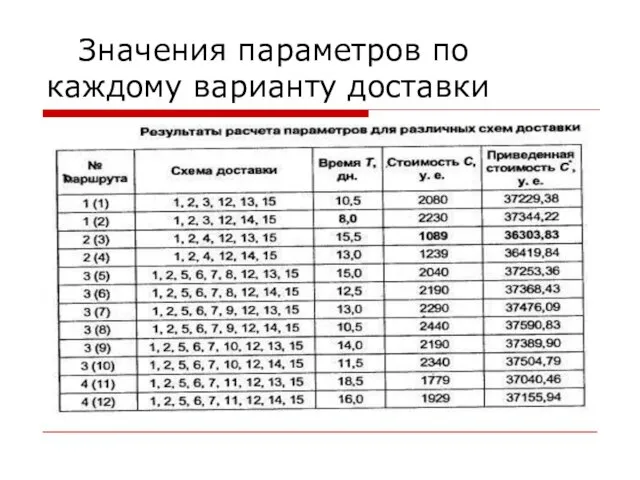
Значения параметров по каждому варианту доставки

Привидение параметров в относительный вид для получение сопоставимых результатов
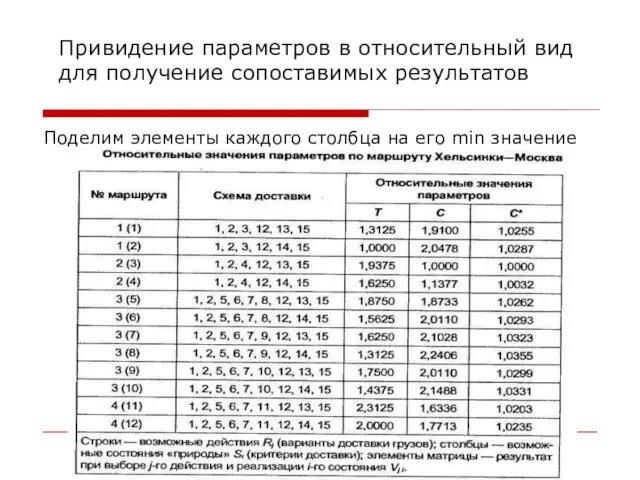
Поделим элементы каждого столбца на его min значение

Критерий Лапласа на примере (определение значения искомых критериев)
Принцип недостаточного основания:
Все состояния природы Si(i=1,…,n) - равновероятны. qi=1/n=1/3
Среднее арифметическое потерь:
M1=1/3 * (1,3125 + 1,9100 + 1,0255)=1,4160
Mj= аналогично.
W=min{Mj(R)}
W – значение параметра, соответствующее варианту доставки груза.
min{Mj} будет соответствовать искомому варианту доставки.

Критерий Вальда на примере (определение значения искомых критериев)
Принцип наибольшей осторожности.
Если Vi – потери, находим в каждой строке находим max{Vji}.
W=minjmaxi{Vji}
Определяем наибольший элемент в каждой строке:
1,9100 - для первого маршрута
2,0478 – для второго

Критерий Сэвиджа на примере (определение значения искомых критериев)
Использование матрицы рисков.
rji=Vij-minj{Vji}
W=minjmaxi{rji}
r11=1,3125-1,00=0,3125
r12=1,9100-1,00=0,9100
r13=1,0255-1,00=0,0255
max rij = 0,9100

Критерий Гурвица на примере (определение значения искомых критериев)
Природа может находиться в самом невыгодном состоянии с вероятностью (1-α)
И в самом выгодном состоянии с вероятностью α.
α – коэффициент доверия.
Если элементы матрицы – потери, то:
W=minj[αminiVji + (1- α) maxiVji]
α=0,5
0,5*1,0255 + 0,5*1,9100=1,4559

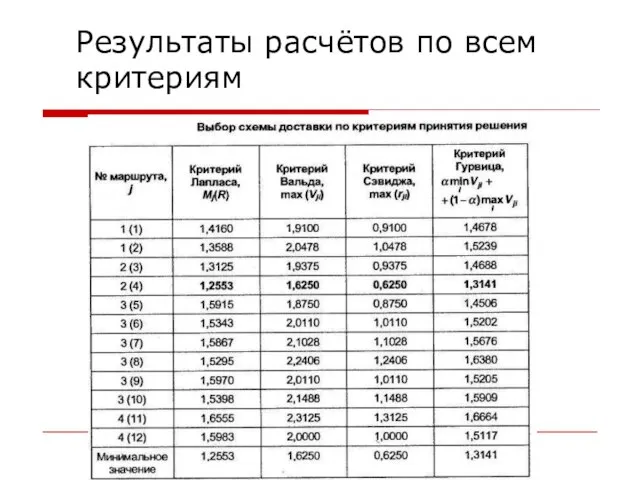
Результаты расчётов по всем критериям