Содержание
- 2. Геометрическая фигура называется простой, если ее можно разбить на конечное число треугольников. Очевидно, что выпуклый плоский
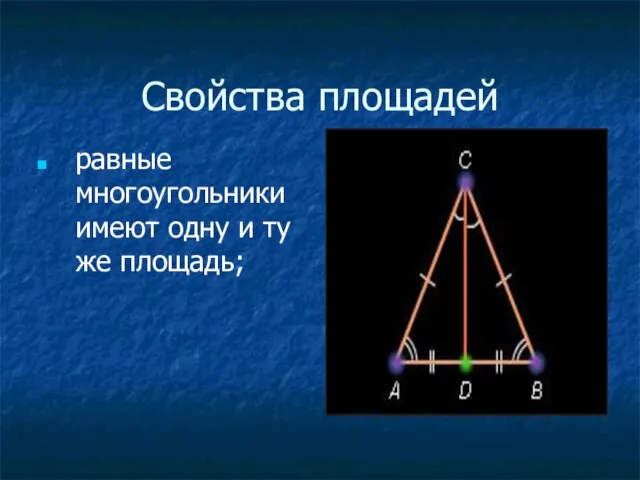
- 3. Свойства площадей равные многоугольники имеют одну и ту же площадь;
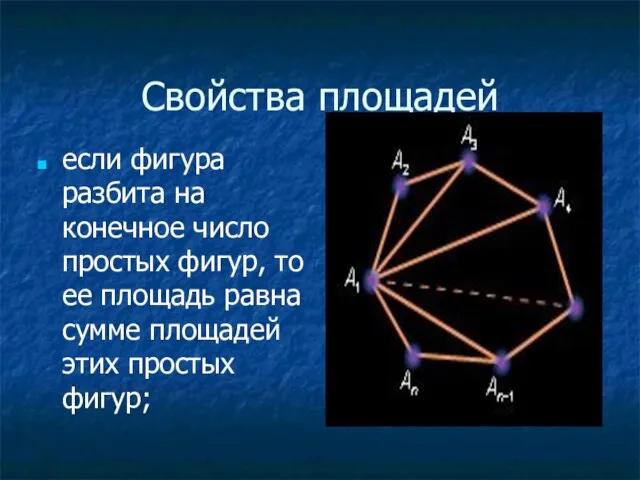
- 4. Свойства площадей если фигура разбита на конечное число простых фигур, то ее площадь равна сумме площадей
- 5. Свойства площадей площадь квадрата со стороной, равной единице измерения, равна единице. 1 1 S квадрата=1
- 6. Измерение площади состоит в сравнении площади SF данной фигуры F с площадью квадрата со стороной, равной
- 7. Фигуры, имеющие одинаковую площадь, называются равновеликими. Площади равных фигур равны.
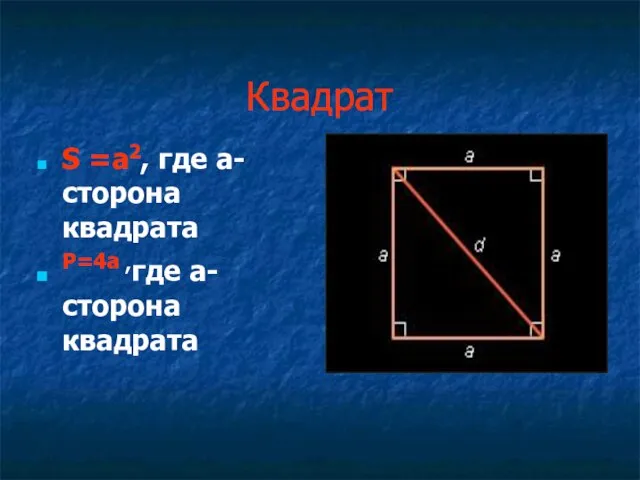
- 8. Квадрат S =a2, где a- сторона квадрата P=4a ,где a- сторона квадрата
- 9. Квадрат S =a2, где a- сторона квадрата P=4a ,где a- сторона квадрата Решить задачу Разность периметров
- 10. ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА.
- 11. А О Е И З М Е Р Е Н И Е О Т Р Е
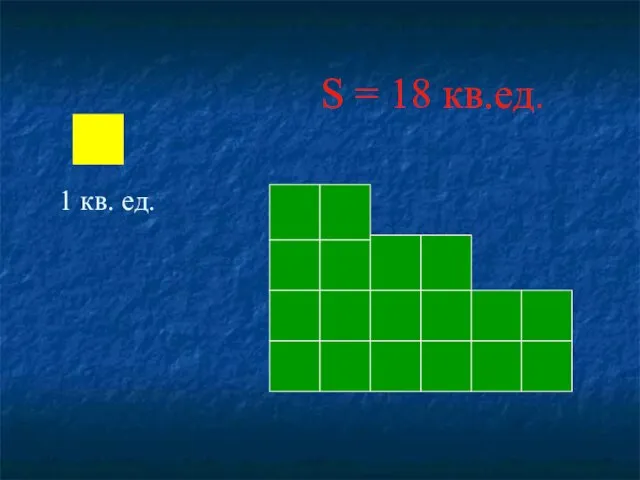
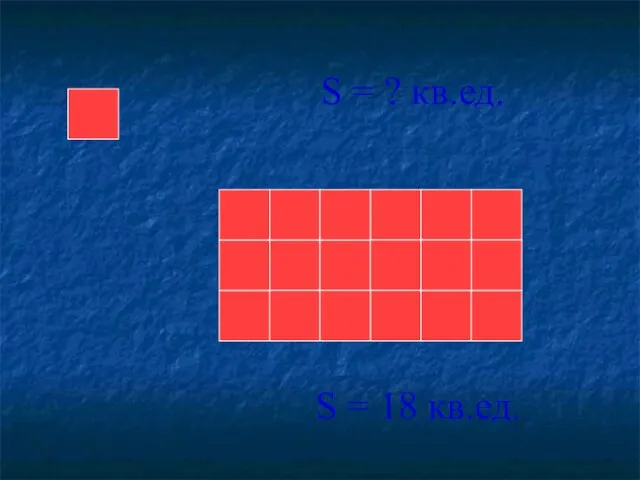
- 12. 1 кв. ед. S = 18 кв.ед.
- 13. РАВНЫЕ ФИГУРЫ
- 14. Равные фигуры – равные площади.
- 16. S = ? кв.ед. S = 18 кв.ед.
- 17. S = 18 кв.ед.
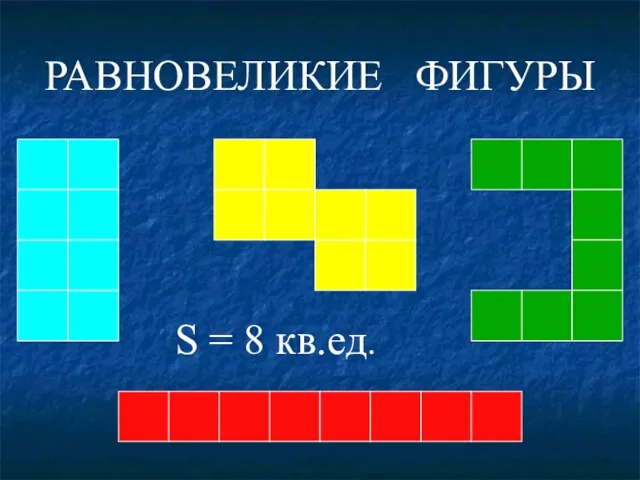
- 18. Фигуры, имеющие равную площадь, называются равновеликими.
- 19. РАВНОВЕЛИКИЕ ФИГУРЫ S = 8 кв.ед.
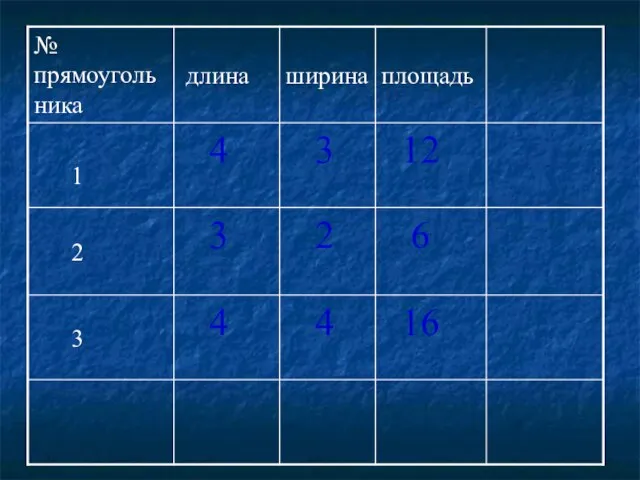
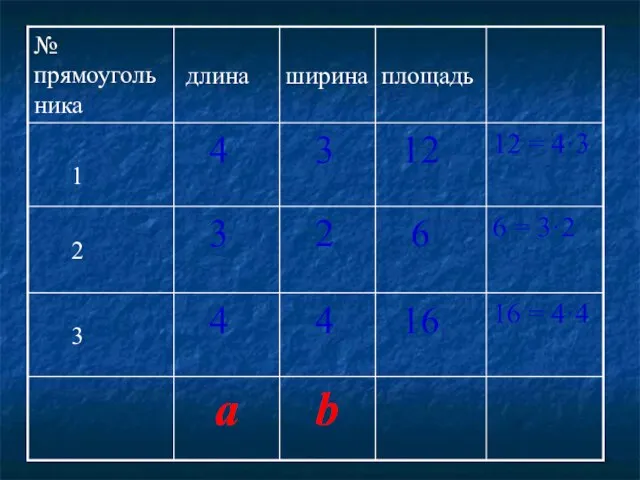
- 21. Найдите длины сторон представленных прямоугольников и их площади. Запишите полученные результаты в таблицу.
- 25. S = a·b Формула площади прямоугольника
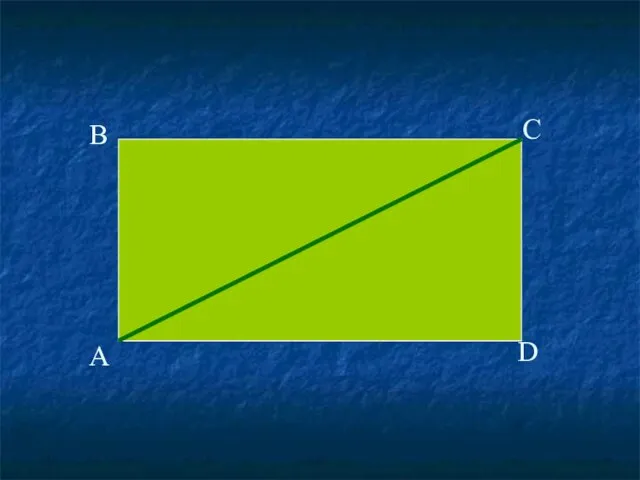
- 26. А В С D
- 27. SΔ= S :2
- 28. Согласны ли вы, что… Равные фигуры имеют равные площади Неравные фигуры имеют различные площади Если фигуры
- 29. 08/18/2023 Площадь треугольника S
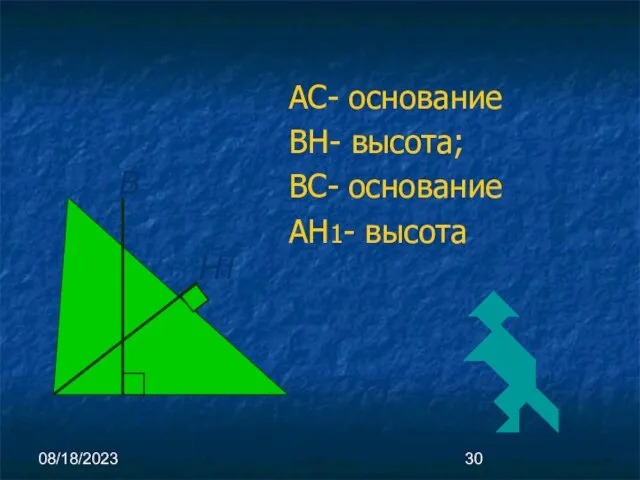
- 30. 08/18/2023 АС- основание ВН- высота; ВС- основание АН1- высота
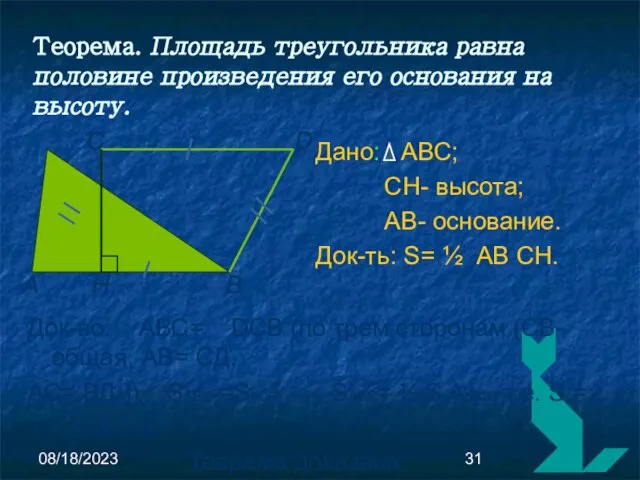
- 31. 08/18/2023 Теорема. Площадь треугольника равна половине произведения его основания на высоту. Док-во: АВС= DСВ (по трем
- 32. 08/18/2023 Следствие 1. ВС- гипотенуза; АВ и АС- катеты. АВС- прямоугольный; SАВС= ½ АВ АС. Площадь
- 33. 08/18/2023 Следствие 2. Если высоты двух треугольников равны, то их площади относятся как основания. ВН= В1Н1
- 34. 08/18/2023 Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как
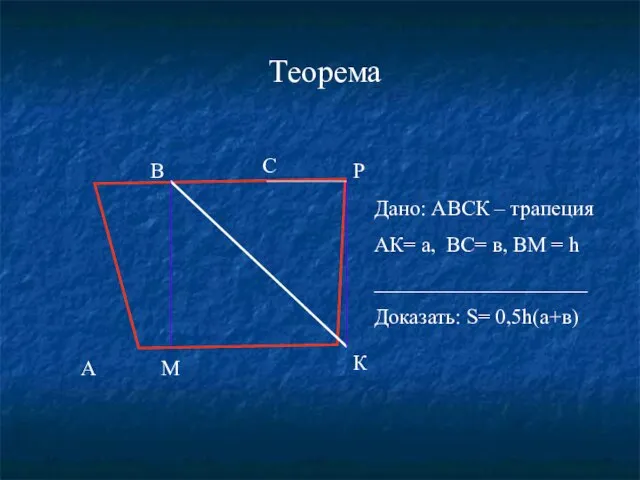
- 35. Площадь трапеции
- 36. А В С К М Р Дано: АВСК – трапеция АК= а, ВС= в, ВМ =
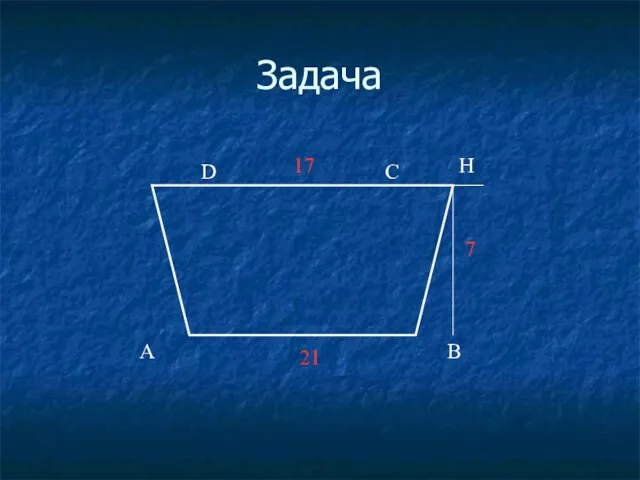
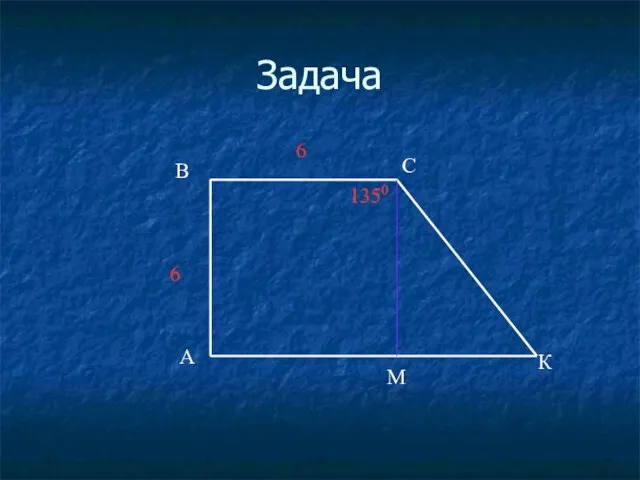
- 37. Задача
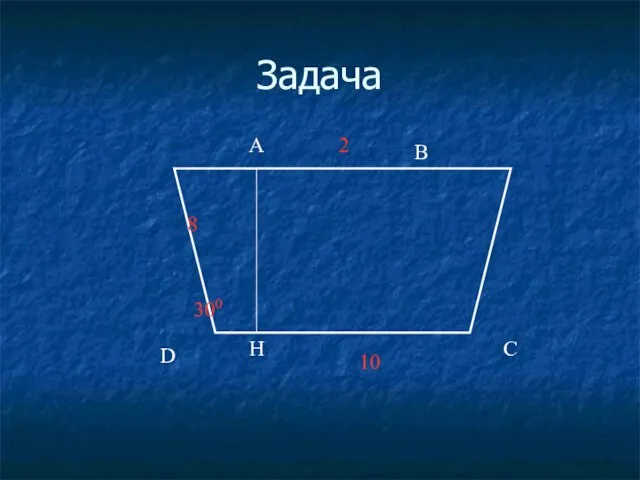
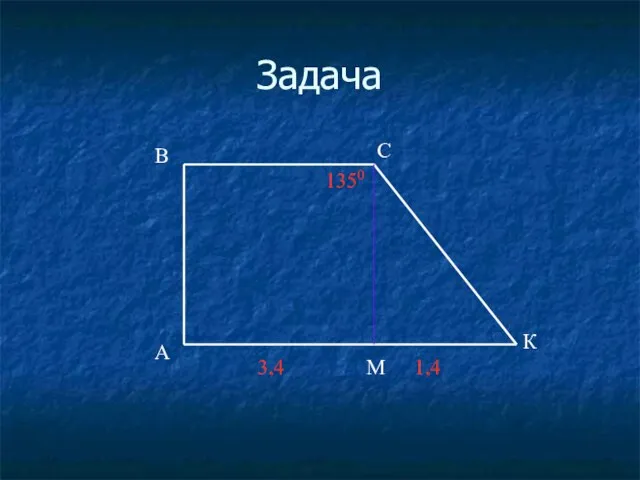
- 38. Задача
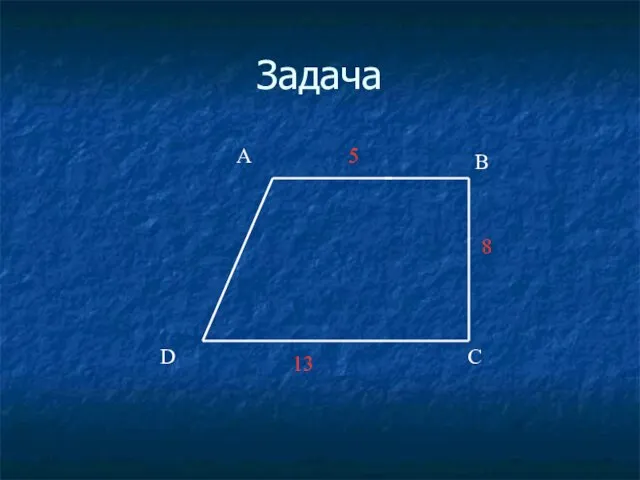
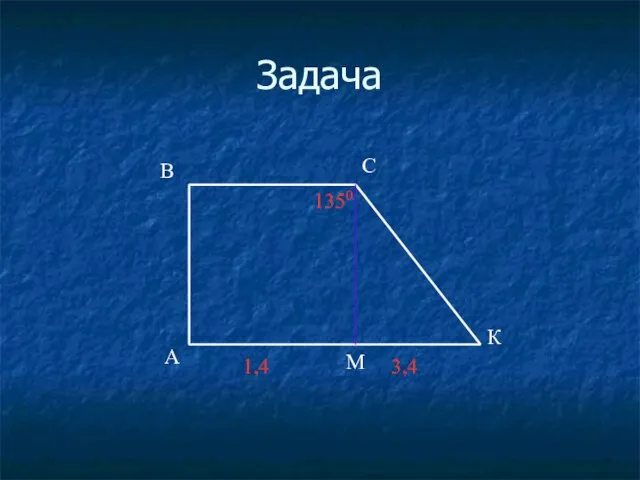
- 39. Задача
- 40. Задача В А С К М
- 41. Задача А В С К М
- 42. Задача А В С К М
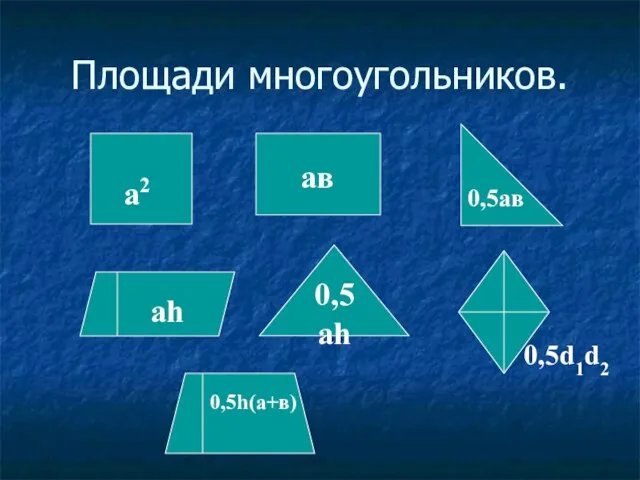
- 43. Площади многоугольников. а2 ав 0,5ав аh 0,5аh 0,5d1d2 0,5h(а+в)
- 44. Cамостоятельная работа Высота и основания трапеции относятся как 5:6:4. Найдите меньшее основание трапеции,если её площадь равна
- 45. Теорема Пифагора Пребудет вечной истина, как скоро Её познает слабый человек! И ныне теорема Пифагора Верна,
- 46. Содержание Формулировка теоремы Доказательства теоремы Значение теоремы Пифагора
- 47. Формулировка теоремы « Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
- 48. Современная формулировка « В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- 49. Доказательства теоремы Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
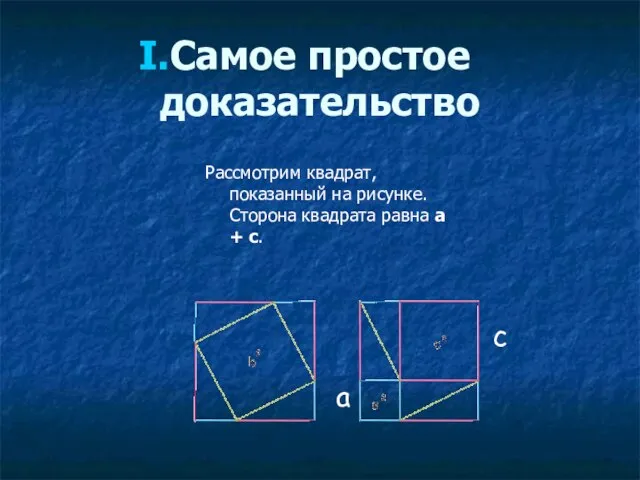
- 50. Самое простое доказательство Рассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c. c a
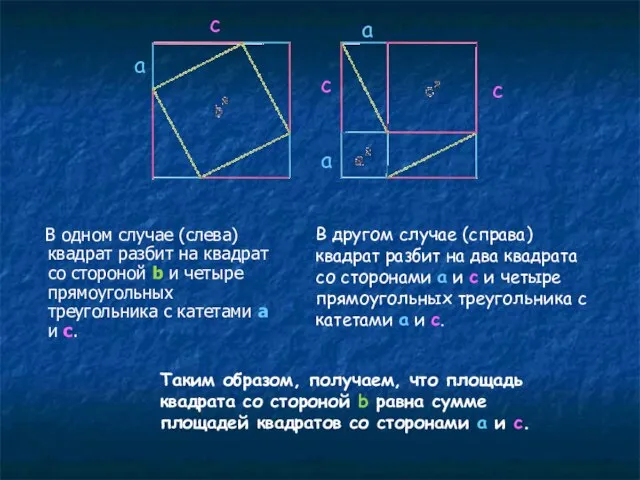
- 51. В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с
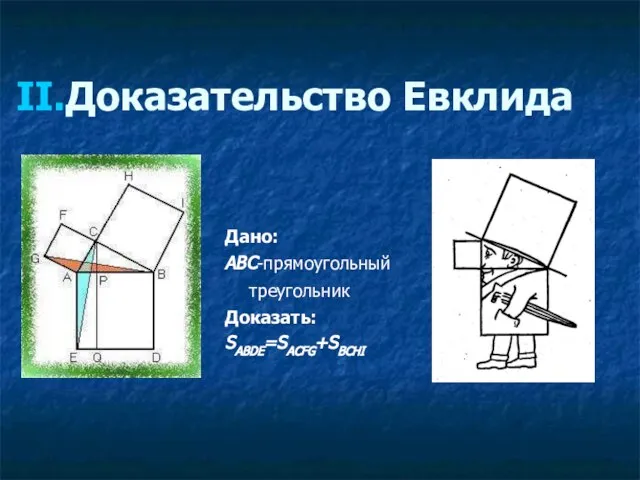
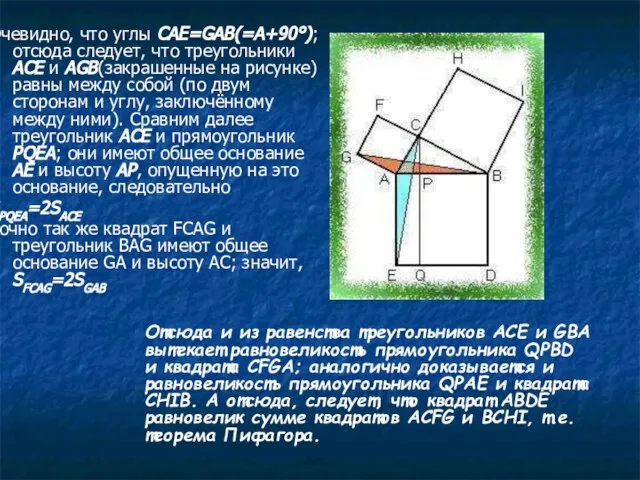
- 52. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать: SABDE=SACFG+SBCHI
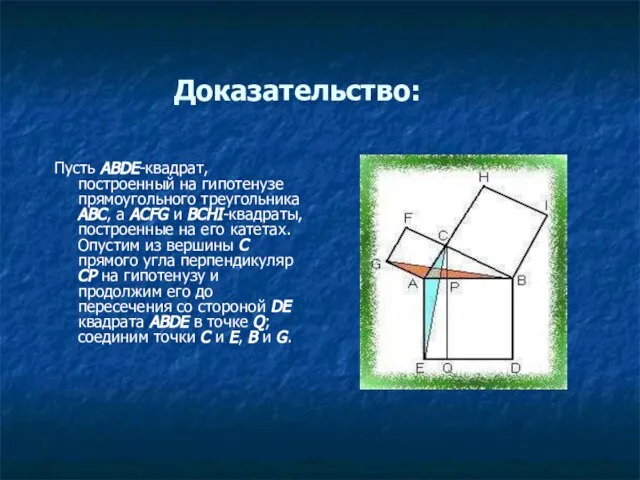
- 53. Доказательство: Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а ACFG и BCHI-квадраты, построенные на его
- 54. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и AGB(закрашенные на рисунке) равны между собой
- 55. Алгебраическое доказательство Дано: ABC-прямоугольный треугольник Доказать: AB2=AC2+BC2 Доказательство: 1) Проведем высоту CD из вершины прямого угла
- 56. Геометрическое доказательство Дано: ABC-прямоугольный треугольник Доказать: BC2=AB2+AC2 Доказательство: 1) Построим отрезок CD равный отрезку AB на
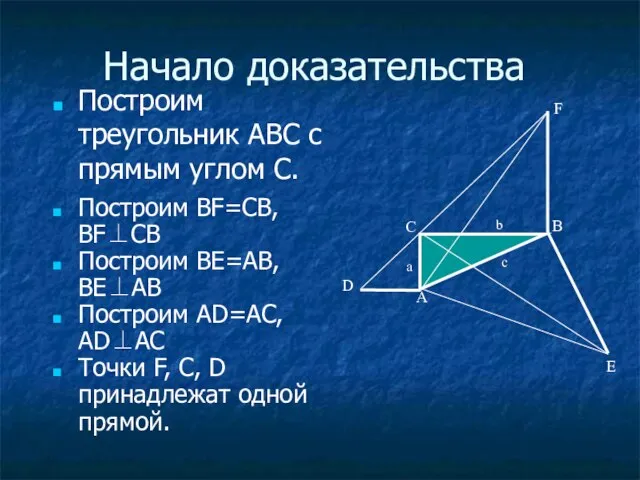
- 57. Построим треугольник ABC с прямым углом С. Начало доказательства Построим BF=CB, BF⊥CB Построим BE=AB, BE⊥AB Построим
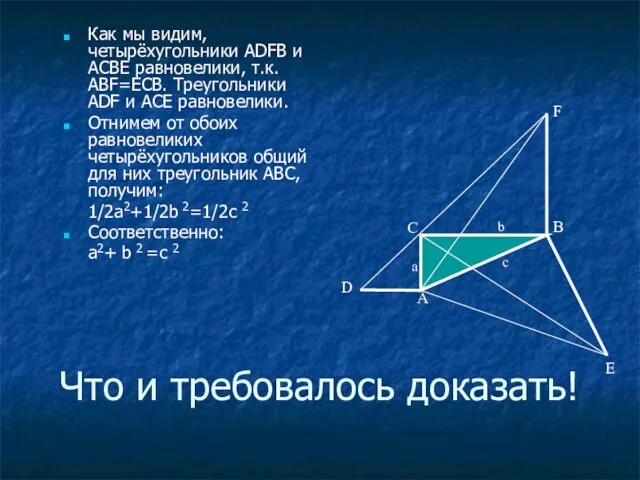
- 58. Что и требовалось доказать! Как мы видим, четырёхугольники ADFB и ACBE равновелики, т.к. ABF=ЕCB. Треугольники ADF
- 59. Начало доказательства Площадь данного прямоугольника с одной стороны равна 0.5ab, с другой 0.5pr, где p –
- 60. Что и требовалось доказать! Имеем: 0.5ab=0.5pr=0.5(a+b+c)*0.5(a+b-c) Отсюда следует, что с2= а2+b2
- 61. Значение теоремы Пифагора Теорема Пифагора- это одна из самых важных теорем геометрии. Значение её состоит в
- 62. Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum - ослиный
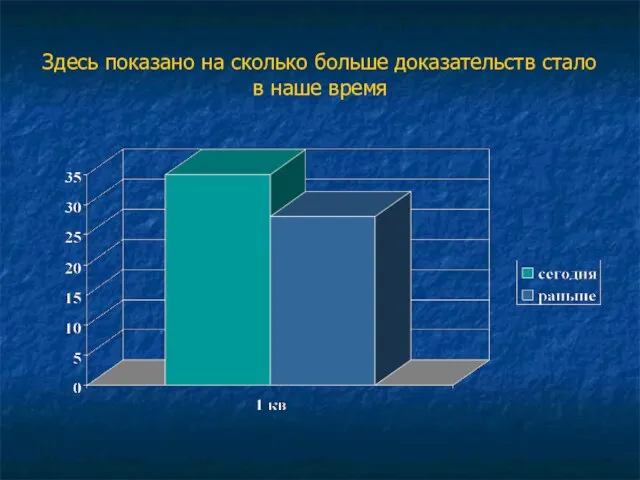
- 63. Здесь показано на сколько больше доказательств стало в наше время
- 64. Подведём итоги Доказательств теоремы Пифагора очень много и они открываются до сих пор ,так что не
- 65. ТЕОРЕМА ПИФАГОРА ПРИМЕНЕНИЕ
- 66. ОБЛАСТИ ПРИМЕНЕНИЯ Строительство Астрономия Мобильная связь
- 67. Мобильная связь Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в
- 68. Строительство Окна Крыши Молниеотводы
- 69. Молниеотвод Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает
- 70. Окна В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только
- 71. В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то
- 72. Астрономия На этом рисунке показаны точки A и B и путь светового луча от A к
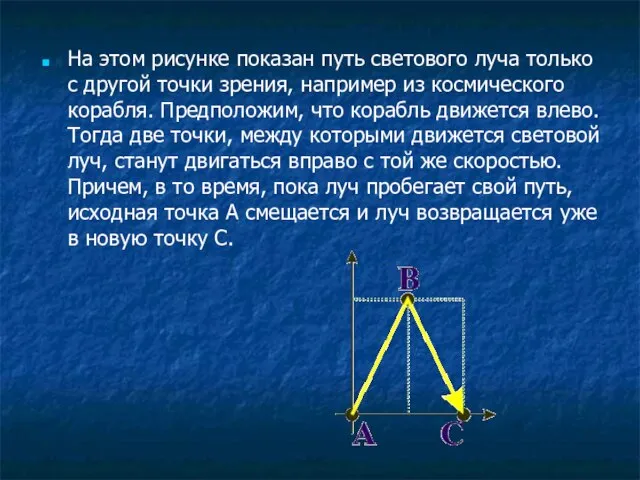
- 73. На этом рисунке показан путь светового луча только с другой точки зрения, например из космического корабля.
- 74. В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя
- 76. Скачать презентацию
















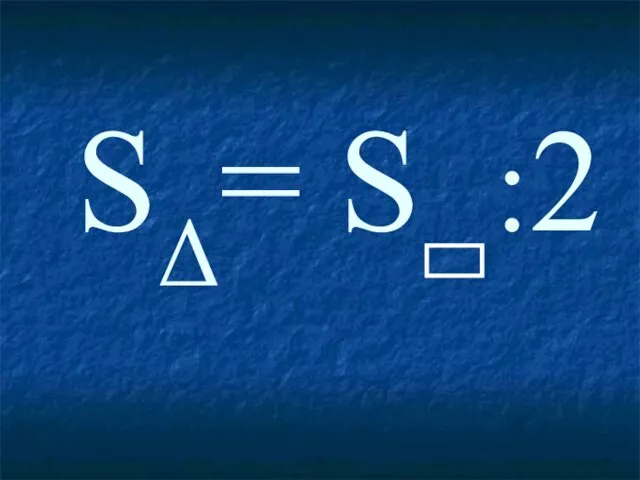




























 Безопасная работа составителя на железной дороге
Безопасная работа составителя на железной дороге Культура России первой половины 19 века
Культура России первой половины 19 века Сидней
Сидней Арифметические действия в двоичной системе счисления
Арифметические действия в двоичной системе счисления Высокодоходные инвестиции в спортивно-тренировочный комплекс
Высокодоходные инвестиции в спортивно-тренировочный комплекс Внедрение ЛЕГО-конструирования в образовательный процесс ДОУ Ергина Д.Г.
Внедрение ЛЕГО-конструирования в образовательный процесс ДОУ Ергина Д.Г.  Установка мини-пруда
Установка мини-пруда Мультимедийная презентация «Пороки человека».
Мультимедийная презентация «Пороки человека». Чевианы треугольникаСвойства медиан
Чевианы треугольникаСвойства медиан Пасхальные каникулы 2011
Пасхальные каникулы 2011 Обкатка машин. Окрашивание
Обкатка машин. Окрашивание Телефония и Умный дом
Телефония и Умный дом Государственно-частное партнерство и долевое финансирование в развитии дорожной инфраструктуры Швеции
Государственно-частное партнерство и долевое финансирование в развитии дорожной инфраструктуры Швеции Музей паровозов
Музей паровозов Строение вещества
Строение вещества Контроль якості металів і зварних з'єднань
Контроль якості металів і зварних з'єднань Царства живой природы
Царства живой природы Открытая Правовая Школа НИУ ВШЭ
Открытая Правовая Школа НИУ ВШЭ Жанры игрового кино
Жанры игрового кино Cancun Underwater Museum – Musa
Cancun Underwater Museum – Musa Модернизация системы дополнительного образования детей в РФ
Модернизация системы дополнительного образования детей в РФ Разработка схемы технологического процесса приготовления фирменного блюда испанской кухни
Разработка схемы технологического процесса приготовления фирменного блюда испанской кухни «Tertium non datur» (лат. «третьего не дано»; одно из двух; или – или) Общешкольный проект Литературной гостиной «Ђ» Участники: обучающиес
«Tertium non datur» (лат. «третьего не дано»; одно из двух; или – или) Общешкольный проект Литературной гостиной «Ђ» Участники: обучающиес Анализ Рынка (2)
Анализ Рынка (2) Презентация на тему Джек Лондон Жизнь и его творчество
Презентация на тему Джек Лондон Жизнь и его творчество  Project on the theme: My sports idol.
Project on the theme: My sports idol. Зачем нужна сменная обувь?
Зачем нужна сменная обувь? Композиция на конкурс . Выбор цветовой гаммы
Композиция на конкурс . Выбор цветовой гаммы