Слайд 2Тема : Прямоугольный параллелепипед

Слайд 3
Цель урока:
1) систематизация и изученного материала, развитие умения и навыков применения

формул площади поверхности и объёма прямоугольного параллелепипеда.
2)развивать пространственное мышление, волю для достижения цели, самостоятельность.
3) воспитывать чувство уверенности в себе.
Слайд 4
План урока
1. Организационный момент
2. Устный счет
3. Работа по теме урока.
4.

Закрепление.
5. Практическая работа.
7. Итог урока
8. Домашнее задание
Слайд 5Поверхность прямоугольного параллелепипеда состоит из 6 граней
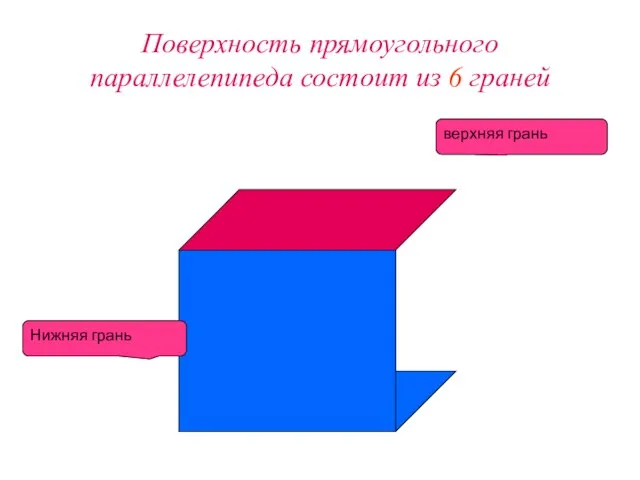
Слайд 6Поверхность прямоугольного параллелепипеда состоит из 6 граней
Нижняя грань
верхняя грань
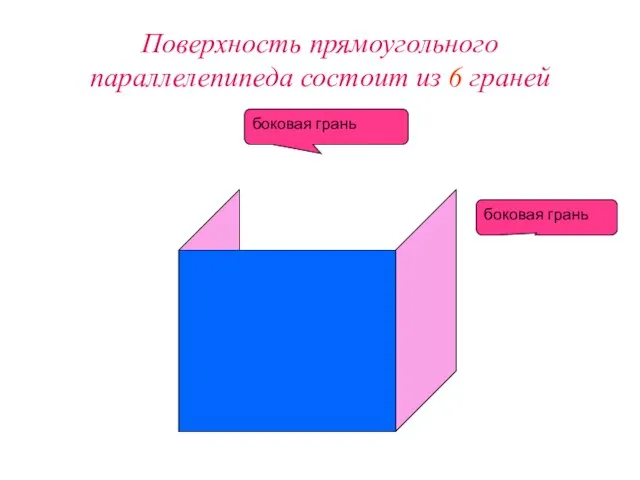
Слайд 7Поверхность прямоугольного параллелепипеда состоит из 6 граней
боковая грань
боковая грань
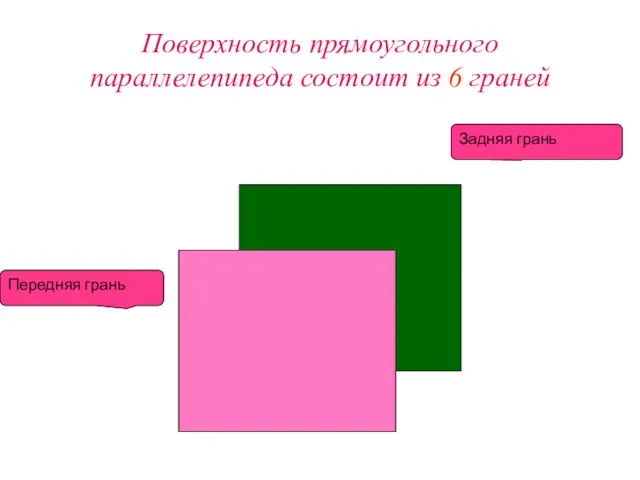
Слайд 8Поверхность прямоугольного параллелепипеда состоит из 6 граней
Задняя грань
Передняя грань
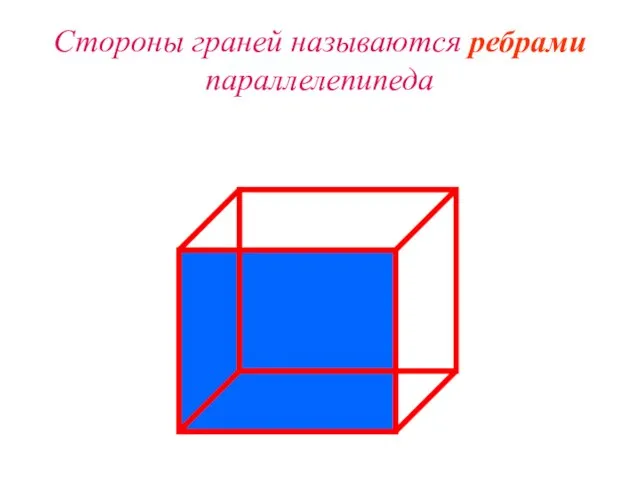
Слайд 9Стороны граней называются ребрами параллелепипеда
Слайд 10Параллелепипед имеет
по 4 равных ребра
а – длина, в – ширина, с
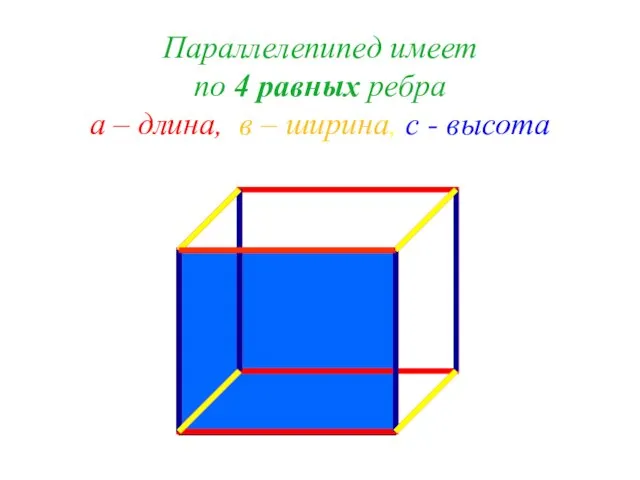
- высота
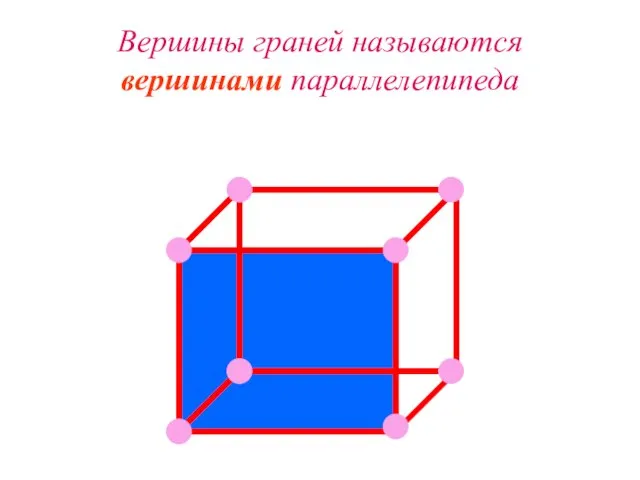
Слайд 11Вершины граней называются вершинами параллелепипеда
Слайд 12Формулы для параллелепипеда.
S=(a•b+a•c+c•b)•2 - площадь поверхности
P=4•(a+b+c) – общий периметр
V=a•b•c – объем

Слайд 13Формулы для куба.
S=6•a² - площадь поверхности
P=12•a – полный периметр
V=a³- объем

Слайд 14
Задача
1. Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 5 дм,
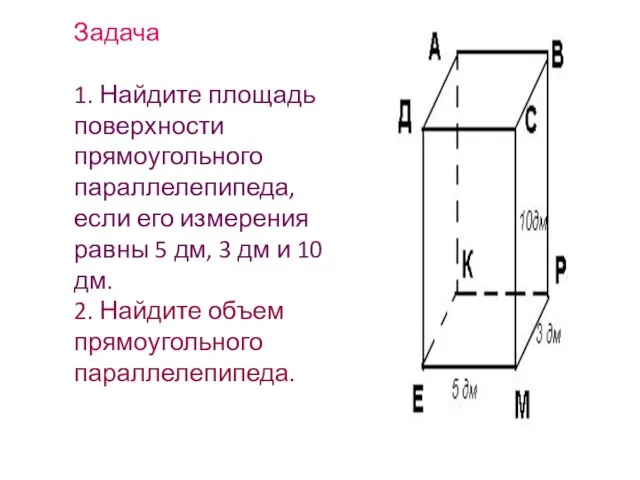
3 дм и 10 дм.
2. Найдите объем прямоугольного параллелепипеда.
Слайд 15Практическая работа
1. Перерисуйте развертку прямоугольного параллелепипеда на плотный лист бумаги, измерения которого

равны а=10 см, в=5 см, с=3 см, вырежьте развертку и склейте из нее прямоугольный параллелепипед.
2. Найдите площадь поверхности и объем прямоугольного
параллелепипеда.
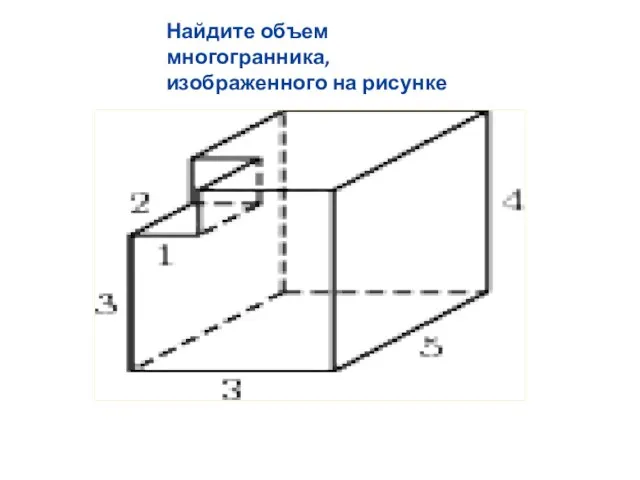
Слайд 16Найдите объем многогранника, изображенного на рисунке .
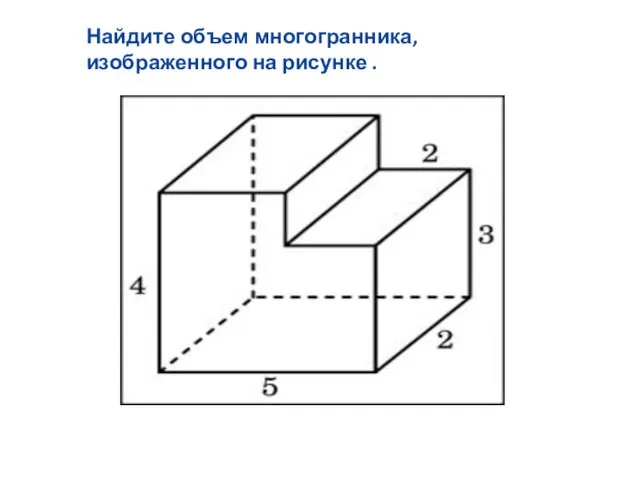
Слайд 17Найдите объем многогранника, изображенного на рисунке .
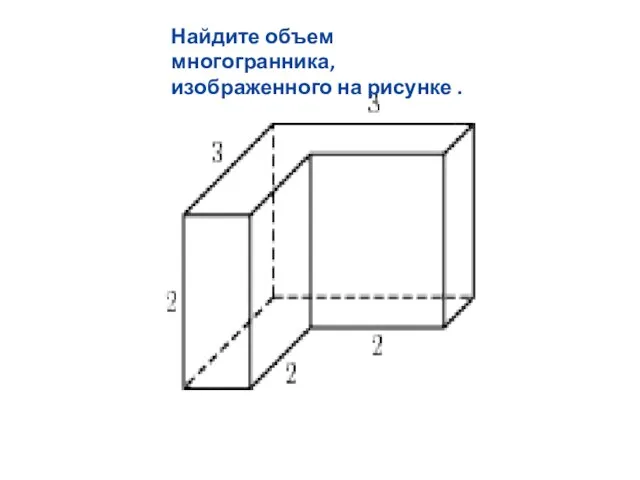
Слайд 18Найдите объем многогранника, изображенного на рисунке .
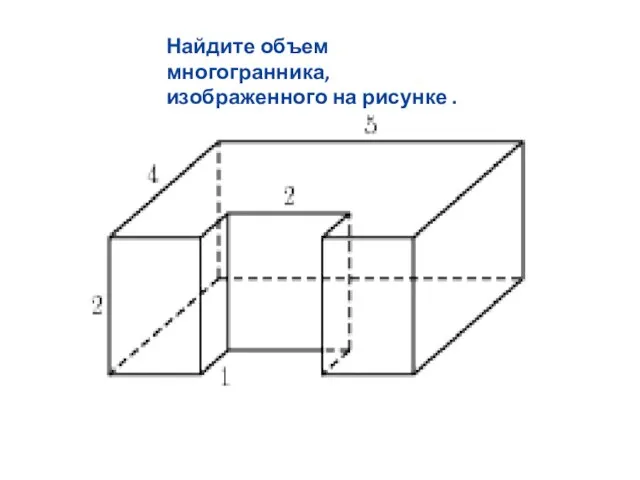
Слайд 19Найдите объем многогранника, изображенного на рисунке
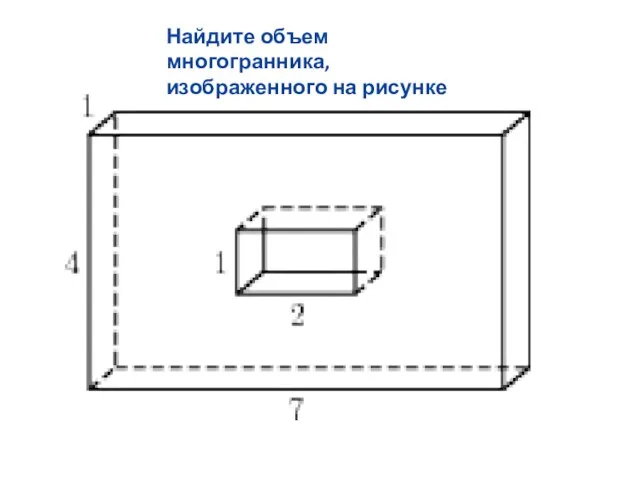
Слайд 20Найдите объем многогранника, изображенного на рисунке
Слайд 21Угадать предмет, название которого произошло от греческого слова, означающего в переводе «игральная

кость»
Слайд 22Историческая справка.
Кубик Рубик - одна из самых известных головоломок. Изобрел его

в 1975 году преподаватель архитектуры из Будапешта Эрне Рубик для развития пространственного мышления у студентов. Головоломка представляет собой куб, как бы разрезанный на 27 одинаковых кубичков. В исходном положении каждая грань куба окрашена в один из шести цветов. Механизм кубика позволяет поворачивать любой слой из девяти кубичков, примыкающих к одной грани куба, вокруг ее центра, при этом цвета граней смешиваются. Задача состоит в том, чтобы вернуть разноцветные грани кубика в исходное положение.
Теоретически из любого состояния в исходное положение можно вернуться не более чем за 23 хода. Лучшие схемы сборки позволяют обойтись примерно 50 поворотами.





















 Chereduyuschiesya_glasnye_v_korne_slova
Chereduyuschiesya_glasnye_v_korne_slova Эмоционально-смысловой метод И.Ю. Шехтера
Эмоционально-смысловой метод И.Ю. Шехтера Презентация на тему Уникумы природных комплексов России
Презентация на тему Уникумы природных комплексов России  Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Произведение искусства в эпоху его технической воспроизводимости
Произведение искусства в эпоху его технической воспроизводимости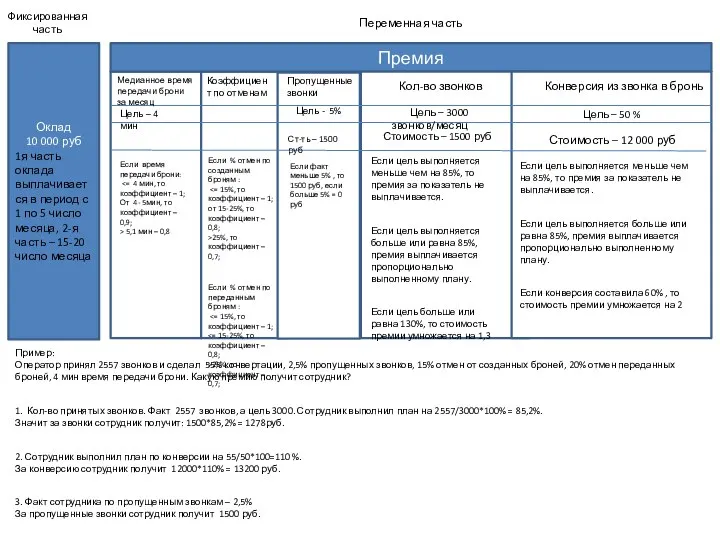 Финансовая мотивация
Финансовая мотивация Выделяя основные элементы общества, их взаимосвязь и взаимодействие, учёные характеризуют общество как
Выделяя основные элементы общества, их взаимосвязь и взаимодействие, учёные характеризуют общество как Картошечка по-деревенски
Картошечка по-деревенски Поздравление с днем рождения внучке
Поздравление с днем рождения внучке Иголка-белошвейка
Иголка-белошвейка Начертательная геометрия и инженерная графика. Тесты
Начертательная геометрия и инженерная графика. Тесты Формирование инфокоммуникационной инфраструктуры Казанского университетского образовательного округа
Формирование инфокоммуникационной инфраструктуры Казанского университетского образовательного округа Социологический факультет МГУ им.Ломоносова
Социологический факультет МГУ им.Ломоносова Добросовестность в ГП
Добросовестность в ГП Метод кейсов
Метод кейсов  Концепция круглогодичного профессионального Индор гольф центра
Концепция круглогодичного профессионального Индор гольф центра Презентация на тему Звёздное небо 1 класс
Презентация на тему Звёздное небо 1 класс Теория организации направления современного развития
Теория организации направления современного развития Что такое ФГТ?
Что такое ФГТ? Fotoreport
Fotoreport Историческая разминка Подготовила: студентка 1 курса группы 1404 Лухманова Ирина
Историческая разминка Подготовила: студентка 1 курса группы 1404 Лухманова Ирина Эволюция темы «маленького человека» в русской литературе
Эволюция темы «маленького человека» в русской литературе Презентация на тему Первый закон термодинамики
Презентация на тему Первый закон термодинамики Методы определения показателей обилия насекомых в луговых /лесных экосистемах
Методы определения показателей обилия насекомых в луговых /лесных экосистемах Презентация на тему Внутреннее строение и размножение рыб
Презентация на тему Внутреннее строение и размножение рыб Презентация на тему Электрическое сопротивление проводника. Удельное сопротивление
Презентация на тему Электрическое сопротивление проводника. Удельное сопротивление Логика, стиль и язык закона
Логика, стиль и язык закона luxe collection. Коллекция препаратов для ухода за кожей лица
luxe collection. Коллекция препаратов для ухода за кожей лица