Элементы_комбинаторики,_статистики_и_теории_вероятностей_

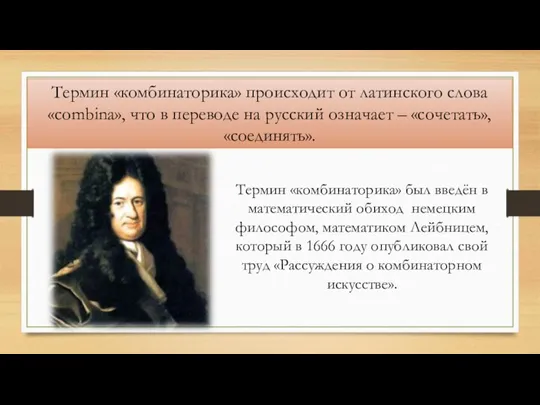
Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Познакомимся с некоторыми
приемами решения комбинаторных задач
решение методом перебора;
решение с помощью дерева возможных вариантов;
решение с помощью комбинаторного правила умножения;
решение с помощью таблиц;
решение с помощью графов.

У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов?
Замечание. При решении для краткости будем писать первые буквы имен.

Составим сначала все пары, в которые входит Вера.
ВЗ, ВМ, ВП, ВС
Выпишем теперь пары, в которые входит Зоя, но не входит Вера.
Далее составим пары, в которые входит Марина, но не входят Вера и Зоя.
Еще одна пара
ЗМ, ЗП, ЗС
МП, МС
ПС
Всего существует 4+3+2+1=10
Решение
Ответ:10 вариантов
Вера
Зоя
Марина
Полина
Света
Получим 4 пары.
Таких пар три.
Их две.
Далее составим пары, в которые входит Полина.

Рассмотрим еще одну задачу. На цветочной клумбе сидели шмель, жук, бабочка и муха. Два насекомых улетели. Какие пары насекомых могли улететь? Укажите все возможные варианты. Сколько таких вариантов?
Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.
ш
ж
б
м

Решение
Всего 3+2+1=6
Ответ:6 вариантов
ш
ш
ш
ж
ж
б
б
б
ж
м
м
м

Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел.
Ответ: 9 чисел.
Приемы решения комбинаторных задач
метод перебора
11;14;17; (начали с 1)
Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?
41;44;47; (начали с 4)
71;74;77; (начали с 7)

Комбинаторные задачи.
1. Дерево вариантов.

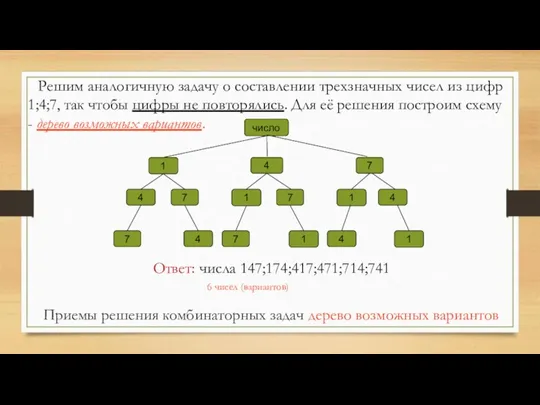
Приемы решения комбинаторных задач дерево возможных вариантов
Решим аналогичную задачу о составлении трехзначных чисел из цифр 1;4;7, так чтобы цифры не повторялись. Для её решения построим схему - дерево возможных вариантов.
число
1
4
7
4
4
7
7
1
1
7
7
1
1
4
4
Ответ: числа 147;174;417;471;714;741
6 чисел (вариантов)

Заметим, что ответ на вопрос, можно получить, не выписывая сами числа. Будем рассуждать так.
Первую цифру можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать двумя способами. Остается приписать одну цифру. Следовательно, общее число искомых трехзначных чисел равно произведению

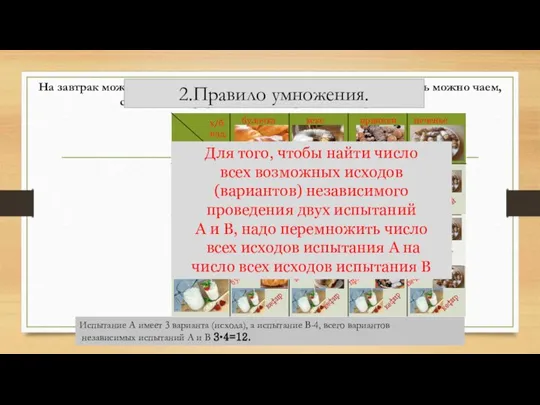
Комбинаторные задачи.
2. Правило умножения.

На завтрак можно выбрать булочку, кекс, пряники или печенье, запить можно чаем, соком или кефиром. Сколько вариантов завтрака есть?
х/б
изд.
напитки
булочка
кекс
пряники
печенье
чай
сок
кефир
чай
чай
чай
чай
кефир
сок
сок
сок
сок
кефир
кефир
кефир
булочка
булочка
булочка
кекс
кекс
кекс
пряники
пряники
пряники
печенье
печенье
печенье
Выбор напитка- испытание А
Выбор хл./бул. изделия.- испытание В
Испытание А имеет 3 варианта (исхода), а испытание В-4, всего вариантов
независимых испытаний А и В 3•4=12.
Для того, чтобы найти число
всех возможных исходов
(вариантов) независимого
проведения двух испытаний
А и В, надо перемножить число
всех исходов испытания А на
число всех исходов испытания В
2.Правило умножения.

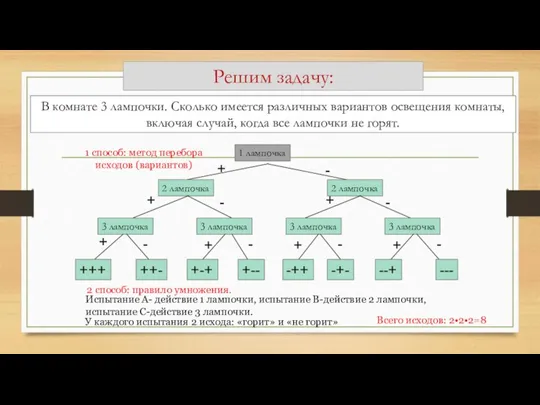
В комнате 3 лампочки. Сколько имеется различных вариантов освещения комнаты, включая случай, когда все лампочки не горят.
1 лампочка
2 лампочка
2 лампочка
+
-
+
-
3 лампочка
3 лампочка
+
-
3 лампочка
3 лампочка
+
-
+
+
+
-
+++
++-
+-+
+--
-++
-+-
--+
---
-
-
1 способ: метод перебора
исходов (вариантов)
2 способ: правило умножения.
Испытание А- действие 1 лампочки, испытание В-действие 2 лампочки,
испытание С-действие 3 лампочки.
Решим задачу:
У каждого испытания 2 исхода: «горит» и «не горит»
Всего исходов: 2•2•2=8

Семейный ужин.
В семье 6 человек, а за столом в кухне 6 стульев. Было решено каждый вечер перед ужином рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?
№1
№2
№3
№4
№5
№6
6
5
4
3
2
1
6•5•4•3•2•1=
720дн.
-почти 2 года

«Если объект А можно выбрать m способами, а другой объект В можно выбрать k способами, то объект «А и В» можно выбрать m ∙ k способами».
Мы нашли ответ на вопрос, используя так называемое комбинаторное правило умножения

У куклы Светы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светы?
Решение. 3·5 = 15
Комбинаторное правило умножения

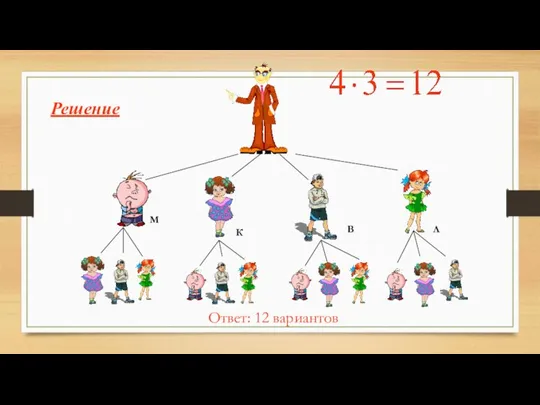
Решите задачу, используя
дерево возможных вариантов
В класс пришли четыре новых ученика Миша, Катя, Вася, Лиза. С помощью дерева возможных вариантов покажи, все возможные варианты расположения четырех учеников за одной партой. Сколько вариантов выбора будет?
Л
В
К
М

Ответ: 12 вариантов
Решение
М
В
К
Л

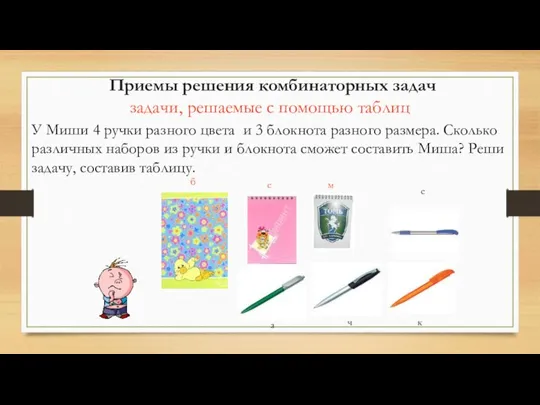
У Миши 4 ручки разного цвета и 3 блокнота разного размера. Сколько различных наборов из ручки и блокнота сможет составить Миша? Реши задачу, составив таблицу.
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
м
с
б
с
з
ч
к

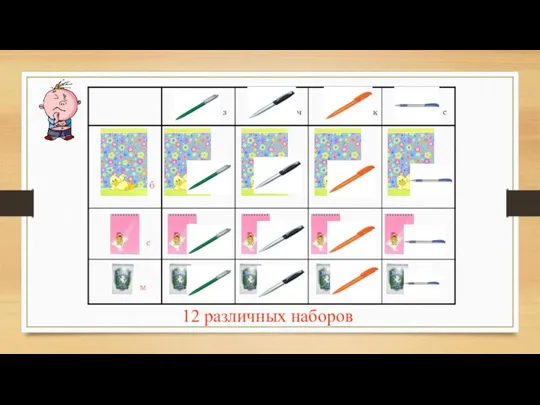
12 различных наборов
м
с
б
з
ч
к
с

Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
Ответ:15 чисел (5·3)
1
2
4
5
9
0
2
4
10
14
12
20
22
24
40
42
44
50
52
54
90
92
94

о
ГРАФ – совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи – как дуги, или ребра.
вершины
ребра

Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал руку. Сколько всего было сделано рукопожатий?
Ответ:10 рукопожатий

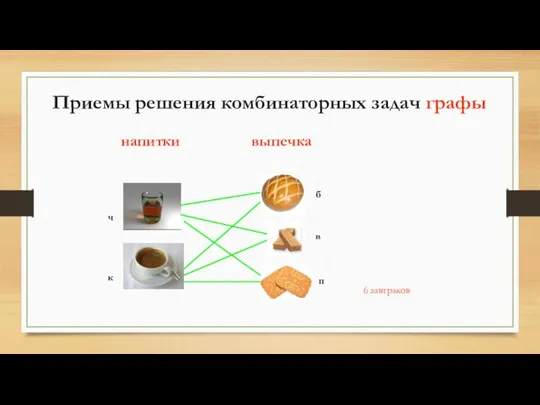
Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая, кофе, булочки, печенья и вафель?
Решите задачу, используя граф
ч
к
б
п
в

6 завтраков
напитки
выпечка
ч
к
б
п
в
Приемы решения комбинаторных задач графы

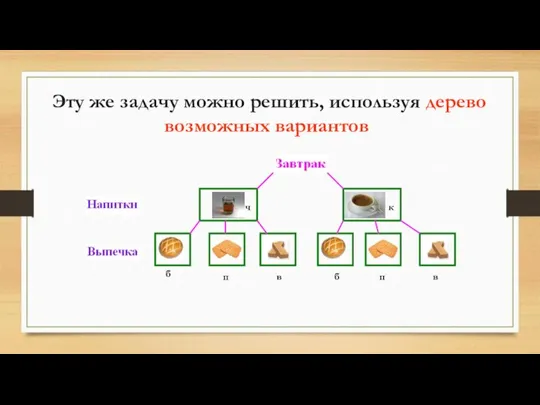
ч
к
б
б
п
п
в
в
Эту же задачу можно решить, используя дерево возможных вариантов

ч
ч
ч
ч
к
к
к
к
п
п
п
б
б
б
в
в
в
Решение задачи с помощью таблицы

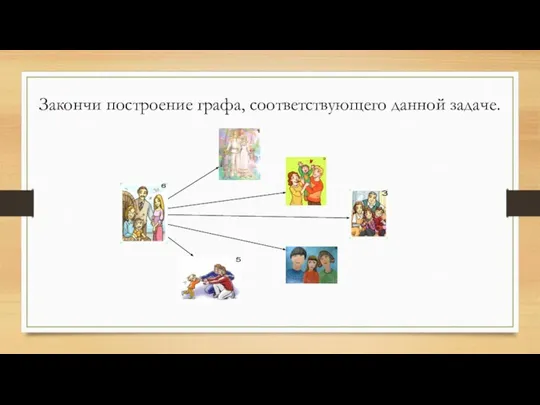
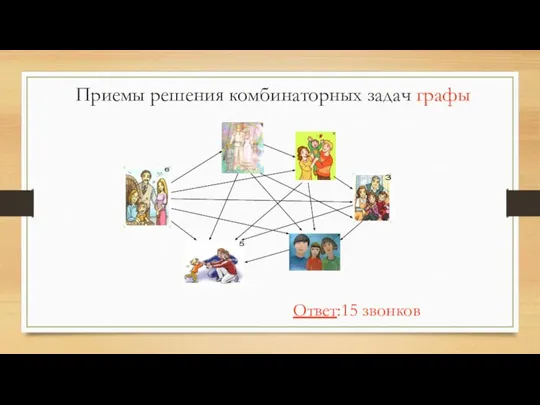
Шесть семей уехали отдыхать в разные города. Приехав к месту отдыха, они поговорили друг с другом по телефону. Сколько звонков было сделано?
Решите задачу, используя граф

Закончи построение графа, соответствующего данной задаче.

Приемы решения комбинаторных задач графы
Ответ:15 звонков

–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
Ответ:15 звонков
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц

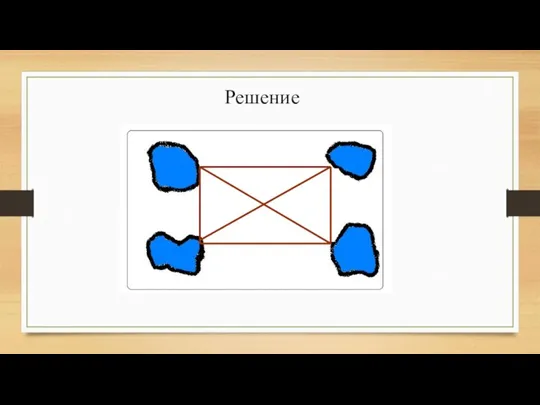
В парке 4 пруда. Было решено засыпать песком дорожки между ними так, чтобы можно было пройти от одного пруда к другому кратчайшим путем, т.е. не нужно было идти в обход.
Задание: покажи, какие дорожки надо сделать.
Графы

Решение

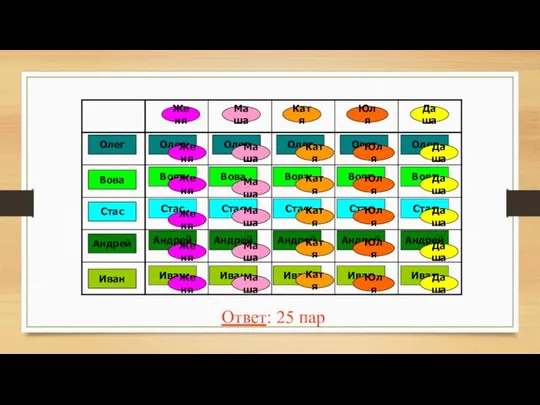
В танцевальном кружке занимаются пять девочек: Женя, Маша, Катя, Юля и Даша и
пять мальчиков: Олег, Вова, Стас, Андрей и Иван. Сколько различных танцевальных пар можно составить? Заполни таблицу.
Задачи, решаемые
с помощью таблиц

Ответ: 25 пар
Женя
Маша
Катя
Юля
Даша
Олег
Вова
Стас
Андрей
Иван
Олег
Олег
Олег
Олег
Олег
Вова
Вова
Вова
Вова
Вова
Стас
Стас
Стас
Стас
Стас
Андрей
Андрей
Андрей
Андрей
Андрей
Иван
Иван
Иван
Иван
Иван
Женя
Женя
Женя
Женя
Женя
Маша
Маша
Маша
Маша
Маша
Катя
Катя
Катя
Катя
Катя
Юля
Юля
Юля
Юля
Юля
Даша
Даша
Даша
Даша
Даша

На завтрак Миша может выбрать: плюшку, бутерброд, пряник, или кекс, а запить он может: кофе, соком, кефиром. Сколько возможных вариантов завтрака?
Ответ:12 (4·3=12)

Тест «Комбинаторные задачи»
1) Сколькими способами можно расставить 3 различные книги на книжной полке?
а) 12 б) 6 в) 9 г) 4
2) В магазине "Все для чая" есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
а) 15 б) 8 в) 9 г) 12
3) Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0; 1 и 2?
а) 12 б) 4 в) 6 г) 24
4) Государственные флаги некоторых стран состоят из трёх горизонтальных полос разного цвета. Сколько существует различных вариантов флагов с белой, синей и красной полосой?
а) 3 б) 4 в) 9 г) 6
5) При встрече 4 школьника обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
а) 6 б) 8 в) 12 г) 4

Проверка !

Комбинаторные задачи.
3. Факториалы и перестановки.

Определение.
Произведение подряд идущих первых n
натуральных чисел обозначают n! и называют
«эн факториал»: n!=1•2•3•…•(n-1)•n.
2!=
1•2=
2
3!=
1•2•3=
6
4!=
1•2•3•4=
24
5!=
1•2•3•4•5=
6!=
120
1•2•3•4•5•6=
720
7!=
1•2•3•4•5•6•7=
5040

Сколькими способами 4 вора могут по одному разбежаться на все 4 стороны.
2
1
3
4
N
O
W
S
Банк
4
3
2
1
1•2•3•4=4!=24
Их разыскивает полиция…

Расписание уроков.
В 9 классе в среду 7 уроков: алгебра, геометрия, литература, русский язык, английский язык, биология и физкультура. Сколько вариантов расписания можно составить?
Расставляем предметы по порядку
Алгебра
7
Геометрия
6
Литература
5
Русский язык
4
Английский язык
3
Биология
2
1
Физкультура
Всего вариантов расписания
1•2•3•4•5•6•7=
=5040
7!=

Перестановки и их число.
Теорема о перестановках элементов конечного множества.
n различных элементов можно расставить
по одному на n различных мест ровно
n! способами.
Определение.
Перестановкой называется множество из n элементов, записанных в определённом порядке.

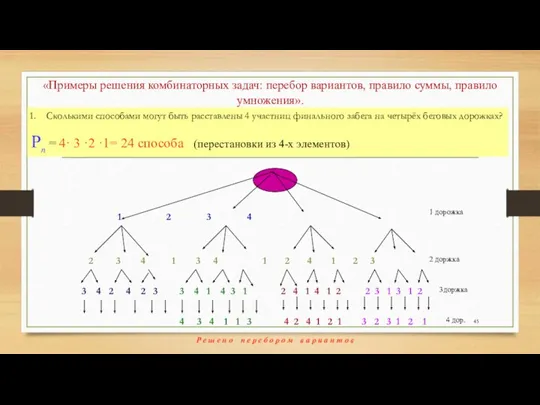
«Примеры решения комбинаторных задач: перебор вариантов, правило суммы, правило умножения».
Сколькими способами могут быть расставлены 4 участниц финального забега на четырёх беговых дорожках?
Рп = 4· 3 ·2 ·1= 24 способа (перестановки из 4-х элементов)
1 2 3 4
2 3 4 1 3 4 1 2 4 1 2 3
3 4 2 4 2 3
4 3 4 2 3 2
3 4 1 4 3 1
4 3 4 1 1 3
2 4 1 4 1 2
4 2 4 1 2 1
2 3 1 3 1 2
3 2 3 1 2 1
1 дорожка
2 доржка
3доржка
4 дор.
Р е ш е н о п е р е б о р о м в а р и а н т о в

Перестановки
Перестановкой из п - элементов называется комбинации, отличающиеся друг от друга лишь порядком следования элементов
Рп- число перестановок (Р первая буква французского слова permutation- перестановка)
Рп= n·(n-1)·(n-2)·(n-3)·(n-4)·. . .·3 ·2 ·1= n!
Рп = n!
В математике принято считать 0! =1 и 1! = 1

Размещения
Пусть имеется 4 шара и 3 пустых ячейки. Обозначим шары буквами a, b, c, d. В пустые ячейки можно по разному разместить три шара из этого набора.
Выбирая по-разному первый, второй и третий шары, будем получать различные упорядоченные тройки шаров
Каждая упорядоченная тройка, которую можно составить из четырёх элементов называется размещением из четырёх элементов по три

Сколько же размещений можно составить из 4-х элементов (abcd) по три?
abc abd acb acd adb adc
bac bad bca bcd bda bdc
cab cad cba cbd cda cdb
dab dac dba dbc dca dcb
Р е ш е н о п е р е б о р о м в а р и а н т о в

Можно решить и не выписывая самих размещений:
первый элемент можно выбрать четырьмя способами, так им может быть любой элемент из четырёх;
для каждого первого второй можно выбрать тремя способами;
для каждых первых двух можно двумя способами выбрать третий элемент из двух оставшихся.
Получаем
= 4·3·2 = 24
Решено с использованием п р а в и л а у м н о ж е ни я

Сочетания
Сочетанием из n элементов по k называют любое множество, составленное из k элементов, выбранных из n элементов
В отличии от размещений в сочетаниях не имеет значение порядок элементов. Два сочетания отличаются друг от друга хотя бы одним элементом

Р е ш и з а д а ч и:
1. На плоскости отмечено 5 точек.
Сколько получится отрезков, если соединить точки попарно?
2. На окружности отмечено п точек. Сколько существует треугольников с вершинами в этих точках?

Статистика: дизайн информации.

«Кто владеет информацией, тот правит миром»
Ф. Бекон
В век бесконечного потока информации крылатое выражение Ф. Бекона приобретает особый смысл. Мало владеть какой-то информацией, её нужно правильно использовать. Но часто информация трудна для восприятия: она не наглядна, занимает много места, никак не упорядочена и т.д. А значит, она не может принести пользу. Единственный разумный выход – преобразовать первоначальную информацию. Значительную часть подобного преобразования берёт на себя статистика.
Статистика — отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) данных.
Научимся способам первоначальной обработке информации.

Задача
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 15, 14.
Обработайте эти данные.
Обработать данные – значит:
упорядочить;
группировать;
составить таблицы распределения;
построить график распределения;
составить паспорт данных.

Что такое статистика?
Статистика- дизайн информации.
Статистика – получение, обработка, анализ и публикация информации, характеризующей количественные закономерности жизни в обществе в неразрывной связи с их количественным содержанием.
Энциклопедический словарь.

Задачи статистики:
1) обработка информации;
2) получение и хранение информации;
3)выработка различных прогнозов;
4)оценка достоверности прогнозов и т.д.

Статистические методы обработки информации:
4)Получение «паспорта» данных измерения, в котором собраны основные числовые характеристики полученной информации.
3)Построение графиков распределения данных.
2)Составление таблиц распределения данных.
1) Упорядочение и группировка измерений.

1. Группировка информации

Упорядочение.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
Наименьшая сумма баллов равна 12 (за 4 экзамена получены «3»), наибольшая сумма – 20 (4 экзамена по «5»).
Суммы от 12 до 20 составляют полный ряд данных. Один из результатов измерения называется его вариантой.
Расположим варианты по возрастанию:
12, 13, 13, 14, 14, 14, 16, 16, 16,17, 17, 18, 19, 19, 20.

100 20 30 40 50 30 80 90 40
50 20 50 30 30 50 60 60 50
30 40 60 50 100 60 90 10 20 50
80 20 40 50 10 50 40 30 40
60 120 30 40 60 20 60 10 50 60
1)Заявлено ли время менее 10 минут?
2)Заявлено ли время более 180 минут?
У 50 рабочих городского предприятия попросили оценить время, которое они в среднем тратят на проезд от дома до работы. Получились следующие данные в минутах (с точностью до 10 минут).

Группировка.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
Наименьшая сумма баллов равна 12 (за 4 экзамена получены «3»), наибольшая сумма – 20 (4 экзамена по «5»).
Суммы от 12 до 20 составляют полный ряд данных. Один из вариантов измерения называется его вариантой.
Если среди всех данных конкретного измерения одна варианта встретилась ровно К раз, то число К называют кратностью этой варианты.
Зачем?
кратностью

Выпишем общий ряд данных в измерениях
1) Месяц рождения учеников нашей школы.
1)1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
2) Год рождения ваших родственников и знакомых.
2)1910, 1911, 1912,…, 2008, 2009, 2010, 2011.
3)Годовой процент начислений по вкладам в банке.
3)0,1; 0,2; 0,3;…;0,9; 1; 2; 3;…;14; 15.
4)Начальные буквы в первой строке стихотворения.
4)1, 2, 3,… 28, 29, 30.
Общий ряд данных - это ряд всех значений измерения, заключённых в промежутке от наименьшего возможного до наибольшего возможного значений.
Общий ряд данных.

Варианта измерения- это один из
результатов этого измерения.
Выпишем ряд данных измерения, состоящего из всех разных букв
первых двух строк стихотворений:
«Не говори никому
Всё, что ты видел, забудь…
а, б, в, г, д, е, ё, з, и ,к, л, м, н, о, р, с, т, у, ч, ы, ь.
«Это дерево сосна,
И судьба сосны ясна…
а, б, в, д, е, и, н, о, р, с, т, у, ы, ь, э, я.
100 20 30 40 50 30 80 90 40
50 20 50 30 30 50 60 60 50
30 40 60 50 100 60 90 10 20 50
80 20 40 50 10 50 40 30 40
60 120 30 40 60 20 60 10 50 60
20
30
40
50
60
80
90
100
10
120
Ряд данных измерения- это
ряд из всех его вариант.
Ряд данных измерения.

Кратностью варианты измерения называется число k, которое показывает сколько раз встретилась варианта среди всех данных конкретного измерения.
2 10 2 3 4 5 3 8 9 4
3 5 2 5 3 3 5 6 6 5
3 4 6 5 10 6 9 1 2 5
9 8 2 4 5 1 5 4 3 4
6 12 3 4 6 2 6 1 5 6
Запишем общий ряд данных
Сгруппированный ряд данных.
1,1,2,…,2, 3,…,3, 4,…,4, 5,…,5, 6,…,6, 8,8,8, 9, 9, 10, 10, 12
6
8
7
10
8
1, 2 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
Группировка данных измерения.

2. Табличное представление информации.

Таблицы распределения.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
Наименьшая сумма баллов равна 12 (за 4 экзамена получены «3»), наибольшая сумма – 20 (4 экзамена по «5»).
Суммы от 12 до 20 составляют полный ряд данных. Один из вариантов измерения называется его вариантой.
Таблица, в которой записаны варианты и их кратности, называется таблицей распределения.
Чтобы составить таблицы распределения, удобно сначала упорядочить или сгруппировать данные.

Таблица распределения частот.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
Количество всех измерений (в задаче их 15) называют объёмом измерения.
Частотой варианты называют частное от деления кратности варианты на объём измерения.
Таблица, в которой записаны варианты, их кратности и их частоты, называется таблицей распределения частот.
Чтобы составить таблицы распределения частот, необходимо сначала вычислить кратности вариант.

Таблица распределения частот в процентах.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
Количество всех измерений (в задаче их 15) называют объёмом измерений.
Частотой варианты называют частное от деления кратности варианты на объём измерения.
Чтобы составить таблицы распределений частот в процентах, необходимо сначала вычислить кратности вариант и их частоты.
Можно выразить это частное в процентах.

1,1,2,…,2, 3,…,3, 4,…,4, 5,…,5, 6,…,6, 8,8,8, 9, 9, 10, 10, 12
6
8
7
10
8
1
3
2
6
3
8
4
7
5
10
6
8
8
3
9
2
10
2
12
1
50
2)Табличное представление информации.
Таблица распределения данных
Объём измерения - сумма всех кратностей или количество всех данных измерения.

0,06
0,12
0,16
0,14
0,2
0,04
0,16
0,06
0,04
0,02
1
Часто-
та
Часто-
та, %
6
12
16
14
20
16
4
6
4
2
100
Таблица распределения частот измерения.
Частотой варианты называется отношение её кратности к объёму измерения.
Частота варианты измерения.

3. Графическое представление информации.

График распределения.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
Для наглядности удобно использовать графическое представление информации.
Если по оси Х отметить варианты, по оси У – кратность, то получим ломаную, которая называется полигоном (или многоугольником) распределения данных.

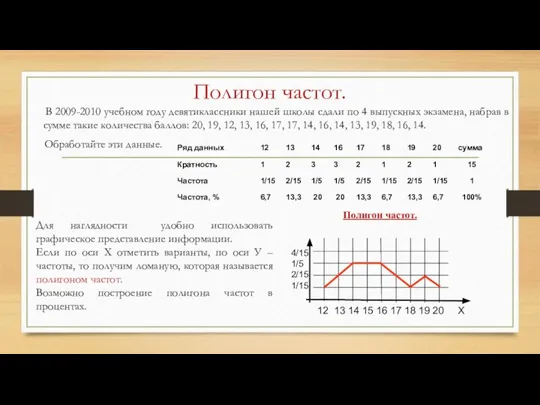
Полигон частот.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
Для наглядности удобно использовать графическое представление информации.
Если по оси Х отметить варианты, по оси У – частоты, то получим ломаную, которая называется полигоном частот.
Возможно построение полигона частот в процентах.

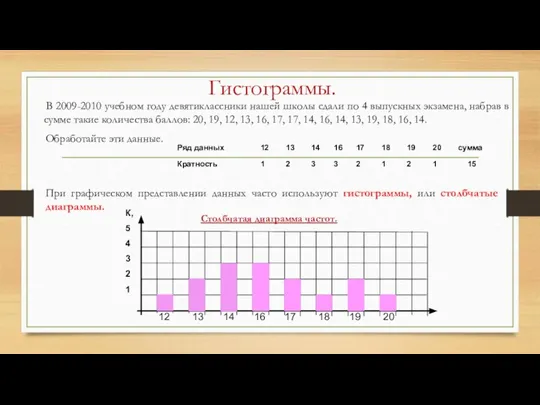
Гистограммы.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
При графическом представлении данных часто используют гистограммы, или столбчатые диаграммы.

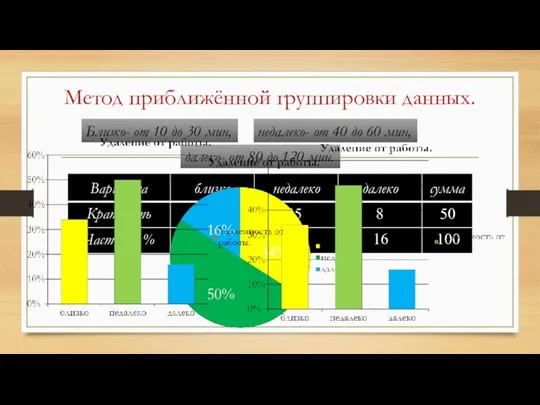
Близко- от 10 до 30 мин,
недалеко- от 40 до 60 мин,
далеко- от 80 до 120 мин.
17
25
8
50
34
50
16
100
34%
50%
16%
Метод приближённой группировки данных.

4. Числовые характеристики данных измерения.

Паспорт данных по таблице распределения.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
Паспорт данных состоит из набора числовых характеристик:
размах (размах – это разность между максимальной и минимальной вариантами);
Размах: R = 20 – 12 = 8
Мода: Мо1 = 14, Мо2 = 16
Медиана: Ме = 16 (искать не удобно)
Среднее: (12*1+13*2+14*4+16*3+17*2+18*1+19*2+20*1)/15 ≈ 15,9
мода (мода – это та варианта, которая встречалась чаще других, та, у которой наибольшая кратность);
медиана (после упорядочения по возрастанию медиана – это варианта, стоящая в середине, если вариант нечётное количество, и среднее арифметическое двух средних вариант, если вариант чётное количество);
среднее значение (среднее арифметическое значений вариант).

Паспорт данных по упорядоченному ряду.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14.
Обработайте эти данные.
Паспорт данных состоит из набора числовых характеристик:
размах (размах – это разность между максимальной и минимальной вариантами);
мода (мода – это та варианта, которая встречалась чаще других, та, у которой больше кратность);
медиана (после упорядочения по возрастанию медиана – это варианта, стоящая в середине, если вариант нечётное количество, и среднее арифметическое двух средних вариант, если вариант чётное количество);
среднее значение (среднее арифметическое значений вариант).
Размах: R = 20 – 12 = 8.
Мода: Мо1 = 14, Мо2 = 16.
Медиана: Ме = 16.
Среднее: (12+13+13+14+14+14+16+16+16+17+17+18+19+19+20) /15 ≈ 15,9.
С помощью упорядоченного ряда данных:
12, 13, 13, 14, 14, 14, 16, 16, 16,17, 17, 18, 19, 19, 20.

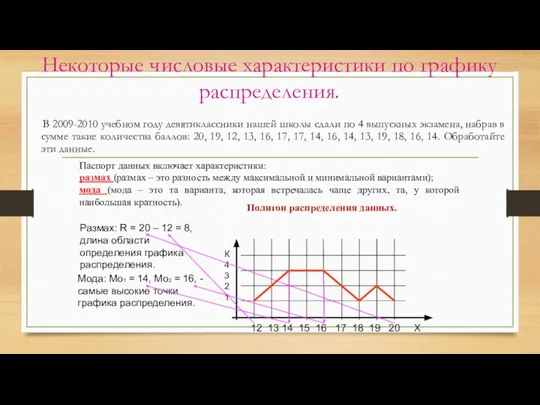
Некоторые числовые характеристики по графику распределения.
В 2009-2010 учебном году девятиклассники нашей школы сдали по 4 выпускных экзамена, набрав в сумме такие количества баллов: 20, 19, 12, 13, 16, 17, 17, 14, 16, 14, 13, 19, 18, 16, 14. Обработайте эти данные.
Паспорт данных включает характеристики:
размах (размах – это разность между максимальной и минимальной вариантами);
мода (мода – это та варианта, которая встречалась чаще других, та, у которой наибольшая кратность).
Размах: R = 20 – 12 = 8, длина области определения графика распределения.
Мода: Мо1 = 14, Мо2 = 16, -
самые высокие точки графика распределения.

Продавец записывал вес арбузов, которые продавал, округляя до целых. Запись выглядит так:
6 5 6 7 8 6 9 8 4 10 5 6 5 6 9 6 10 12 7 10 9 4 8 6 9 10 4 5 9 8 12 9.
Найти объём измерения, составить таблицы распределения, построить график распределения данных, составить паспорт данных.
Объём измерения (количество вариант) – 32.
Таблица распределения
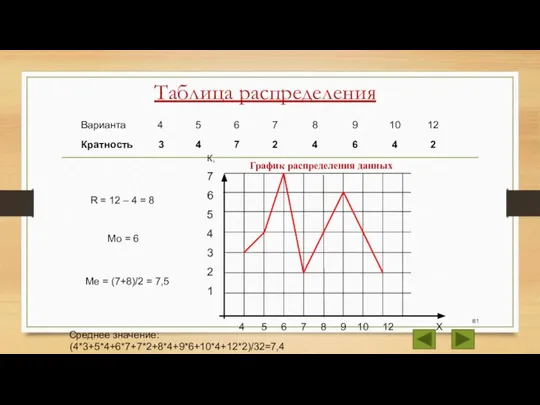
Проверка

Таблица распределения
R = 12 – 4 = 8
Мо = 6
Ме = (7+8)/2 = 7,5
Среднее значение:
(4*3+5*4+6*7+7*2+8*4+9*6+10*4+12*2)/32=7,4

Размахом измерения называется разность между
максимальной и минимальной вариантами.
Полигон распределения частот.
12дес.-1дес.=11дес.
Размах измерения
(И)-110мин.
Модой измерения называется варианта, которая
в измерении встретилась чаще других.
Мода измерения
(И)-50мин.
Медиана измерения
равна (5+6):2=5,5
Частота
варианты
Варианта
1, 2, 3, 4, 5, 6, 8, 9,10, 12
4) Числовые характеристики данных измерения.
Медианой измерения называется варианта, которая
стоит в ряду данных, расположенных по возрастанию,
в середине, если количество вариант нечётно.
В случае чётности количества вариант медиана равна среднему арифметическому двух средних вариант ряда данных.

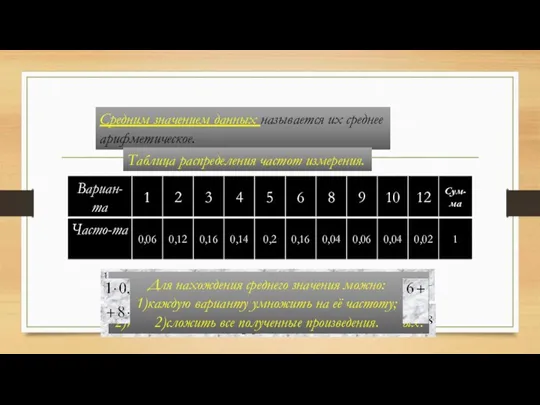
Средним значением данных называется их среднее
арифметическое.
Таблица распределения данных
Среднее значение данных измерения (И)-4,8дес.
или 48минут.
Для нахождения среднего значения нужно:
1)просуммировать все данные измерения;
2)полученную сумму разделить на количество данных.
Таблица распределения частот измерения.
Для нахождения среднего значения можно:
1)каждую варианту умножить на её частоту;
2)сложить все полученные произведения.

На вступительном письменном экзамене по математике можно получить от 0 до 10 баллов. Сорок абитуриентов получили такие оценки:
6 7 7 8 9 2 10 6 5 6
7 3 7 9 9 2 3 2 6 6
6 7 8 8 2 6 7 9 7 5
9 8 2 6 6 3 7 7 6 6
а)Составить общий ряд данных и ряд данных измерения (Э); упорядочить и сгруппировать полученные оценки.
б)Составить таблицы распределения данных и распределения частот.
в)Построить графики распределения данных и распределения частот.
г)Найти размах, моду, среднее значение и медиану.

а)Составить общий ряд данных и ряд данных измерения (Э);
упорядочить и сгруппировать полученные оценки.
Сгруппированный ряд данных.
2,…,2, 3, 3, 3, 5, 5, 6,…,6, 7,…, 7, 8,…,8, 9,…, 9, 10
5
11
9
4
5
Решение задания а).

б)Составить таблицы распределения данных и распределения
частот.
Таблица распределения данных и частот.
Решение задания б).

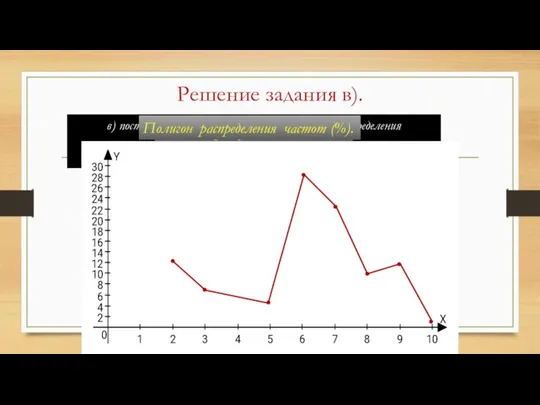
в) построить графики распределения данных и распределения
частот.
Полигон распределения данных.
Полигон распределения частот (%).
Частота варианты
Варианта
Кратность
варианты
Варианта
Решение задания в).

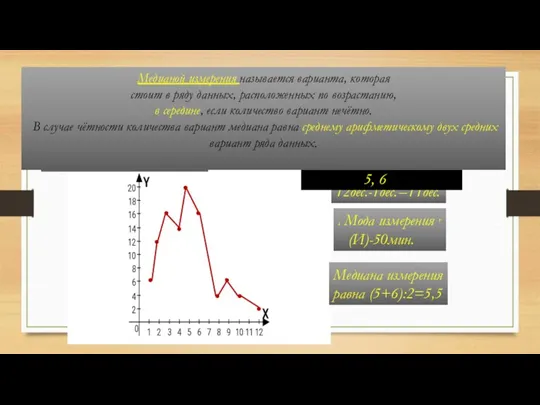
Размах измерения равен 10-2=8
Мода равна 6
Среднее статистическое значение:
Медиана равна (6+7):2=6,5
г)Найти размах измерения, моду, среднее значение и медиану.
( 2∙5+3∙3+5∙2+6∙11+7∙9+8∙4+9∙5+10∙1):40
245:40=6,125
Решение задания г).

5. Дисперсия.

Отклонением от среднего называют разность между рассматриваемым значением случайной величины и средним значением всей совокупности

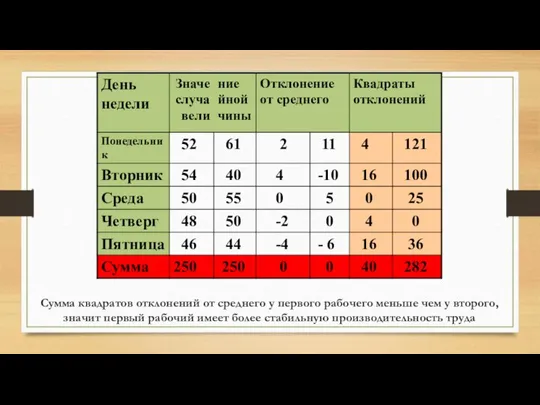
Задача
На место токаря претендуют двое рабочих. Для каждого из них установили испытательный срок, в течение которого они должны были изготовить одинаковые детали. Результаты работы претендентов представлены в таблице:

Средняя производительность труда рабочих одинаковая 50 дет. \ день

Сумма квадратов отклонений от среднего у первого рабочего меньше чем у второго, значит первый рабочий имеет более стабильную производительность труда

Дисперсия
Среднее арифметическое суммы квадратов отклонений от среднего называется дисперсией (dispersus)

Корень квадратный из дисперсии называют средним квадратичным отклонением и обозначают σ
σ =√D

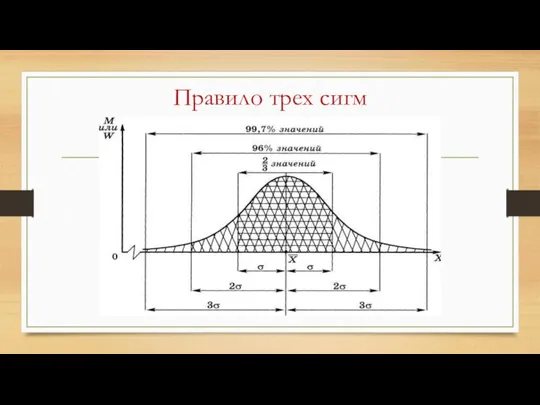
Правило трех сигм

Правило трех сигм
~68% (2\3) всех значений нормально распределенной случайной величины имеют отклонения от среднего по абсолютной величине не превосходящие σ;
~96% всех значений – не превосходящие 2σ;
~99,7% всех значений – не превосходящие 3σ.

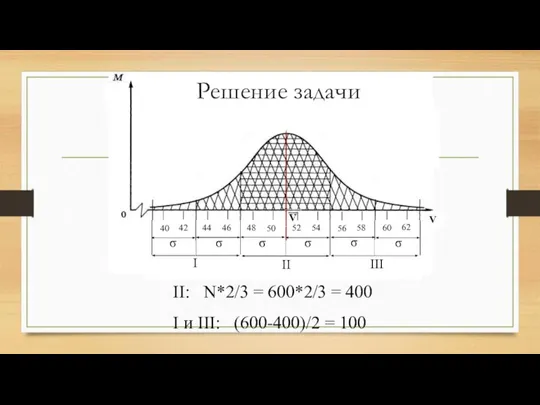
Применение правила трех сигм
ЗАДАЧА.
N=600 спортсменов
V от 40 до 62 размера
Условные I, II, III размеры
Сколько маек каждого из трех условных размеров следует шить?

Решение задачи
II: N*2/3 = 600*2/3 = 400
I и III: (600-400)/2 = 100

Простейшие вероятностные задачи.

Основные понятия
Познание действительности в естественных науках происходит в результате испытаний (эксперимента, наблюдений, опыта).
Испытанием или опытом называется осуществление какого-нибудь определенного комплекса условий, который может быть воспроизведено сколь угодно большое число раз.
Случайным (СС)называется событие, которое может произойти или не произойти в результате некоторого испытания (опыта).
Таким образом, событие рассматривается как результат испытания.
Пример.
Бросание монеты – это испытание.
Появление орла при бросании – событие.

Основные понятия
Два или несколько событий называются равновозможными в данном испытании, если имеются основания считать, что ни одно из этих событий не является более возможным или менее возможным, чем другие.
Пример. При одном бросании одной и той же игральной кости появление 1, 2, 3, 4, 5 и 6 очков - все это события равновозможные.
Два события называются несовместными в данном испытании, если появление одного из них исключает появление другого, и совместными в противном случае.
Пример. В ящике имеются стандартные и нестандартные детали. Берем на удачу одну деталь. Появление стандартной детали исключает появление нестандартной детали. Эти события несовместные.
События А и В называются противоположными, если всякое наступление события А означает ненаступление события В.
Обозначение:
А -событие А
_
А - событие противоположное событию А (читается «не A»).
Пример. Попадание и промах при одном выстреле по цели - события противоположные.
Наблюдаемые нами события различаются по степени возможности их появления и по характеру их взаимосвязи.
Событие называется достоверным, если оно обязательно произойдет в результате данного испытания.
Пример. Получение студентом положительной или отрицательной оценки на экзамене есть событие достоверное, если экзамен протекает согласно обычным правилам.
Событие называется невозможным, если оно не может произойти в результате данного испытания.
Пример. Извлечение из урны белого шара, в которой находятся лишь цветные (небелые) шары, есть событие невозможное.

ИТАК…
Случайное событие (СС)- это событие, которое либо произойдёт, либо нет.
Каждое случайное событие (СС) иметь свою вероятность произойти (сбыться, реализоваться).
Испытание – любое действие, которое может привести к одному или нескольким результатам.
Исход - конечный результат испытания. Значит испытание может иметь один или несколько исходов.
Благоприятный исход - желаемый исход.

1. Подсчёт вероятностей.

Решение различных задач по комбинаторике и теории вероятности

2. Классическое определение вероятности.

Простейшие вероятностные задачи

3. События и множества.

СЛУЧАЙНОЕ СОБЫТИЕ
Определение:
Примеры:
Выпадение орла при подбрасывании монеты.
Выпадение шестёрки при бросании игральной кости.
Выигрыш по данному лотерейному билету.
Выход из строя электролампы в течение определённого отрезка времени.
Некоторое событие (А,В,С,..) называют случайным по отношению к данному опыту, если при осуществлении этого опыта оно либо происходит , либо не происходит.

ДОСТОВЕРНОЕ СОБЫТИЕ
Определение:
Примеры:
Извлечение из урны , где лежат белые шары, белого шара.
Выпадение одного из чисел от 1 до 6 при бросании игральной кости игральной кости.
Событие U называют достоверным, если оно обязательно наступает в результате данного опыта.

Невозможное событие
Определение:
Примеры:
Выпадение числа 7 при бросании игральной кости.
Извлечение черного шара из урны с белыми шарами.
Событие V называется невозможным, если оно заведомо не может произойти в результате данного опыта.

При одном бросании игральной кости могут появиться числа 1,2,3,4,5,6. Каждое из этих событий случайно, т.к. оно может произойти, а может не произойти. Тот факт, что выпадет одно из чисел 1,2,3,4,5,6,- достоверное событие, т.к. при бросании кости оно обязательно произойдет.
Рассмотренные события несовместны (появление одного из их исключает появление другого), единственно возможны (обязательно появится одно из чисел) и равновозможны (у всех чисел шансы появиться одинаковы).

Комбинации событий
Суммой (объединением ) событий А и В называется событие, которое состоит в том, что происходит хотя бы одно из данных событий.
А+В (или А В)

Произведением событий А и В называется событие, которое считается наступившим тогда и только тогда, когда наступают оба события А и В. Произведение А и В обозначают АВ (или А В).
А
В

События А и В называют равносильными (равными) и пишут А=В, если событие А происходит тогда и только тогда, когда происходит событие В.
Противоположное для А событие , которое считается наступившим тогда и только тогда, когда А не наступает.
А
А

ВЕРОЯТНОСТЬ СОБЫТИЯ
Определение:
n- число всех исходов
m – число благоприятных
исходов
Р(А)=
Вероятностью Р(А) события А в опыте с равновозможными элементарными исходами называется отношение числа исходов, благоприятствующих событию А, к числу всех исходов.

События и множества.

4. Вероятность и геометрия.

Вероятность и геометрия.

Экспериментальные данные и вероятности событий.

Полученные из практики величины являются статистическими данными, а вероятность случайного события — моделью реальных ситуаций. Значительно или нет отличается абстрактная модель от практической ситуации? Чтобы ответить на этот вопрос, рассмотрим понятие статистической устойчивости:
Частота появления события отлична от вероятности события для каждого определённого числа повторений опыта.

Явление статистической устойчивости обеспечивает тот факт, что с возрастанием количества повторений опыта вероятность заметного отличия частоты события от его вероятности стремится к нулю. Этот вид устойчивости характерен в случаях, когда подбрасываем монетки, вытаскиваем карты, бросаем игральные кости (кубики) и ждём выпадения конкретного числа очков и для большей части случайных событий.
Благодаря явлению статистической устойчивости соединяются проводимые в реальности, эмпирические испытания с теоретическими моделями этих испытаний.
Так, в истории известны случаи, когда авторство литературатурного произведения подтверждали по частоте употребления в нём оборотов речи, слов и букв.

Статистическая устойчивость показывает, что при осуществлении большого числа повторений испытания рассчитанная частота почти совпадёт с неизвестной нам вероятностью наступления события A. Следовательно, подсчитанная частота примерно равна вероятности события A.

Пример 1
Разумно предположить, что вероятность выпадения орла при бросании монеты равна 0,5. Однако при небольшом числе бросаний это может и не проявиться. Например, при пяти бросаниях орел может выпасть все пять раз (а может и ни разу). Вместе с тем при очень большом числе бросаний орел выпадает примерно в половине случаев. Так в XVIII в. при бросании монеты 4040 раз орел выпал 2048 раз (вероятность 0,5069); в конце XX в. при бросании 10 000 раз - 4979 раз (вероятность 0,4979).
Таким образом, при неограниченном увеличении числа независимых повторений одного и того же опыта в одинаковых условиях частота появления определенного результата случайного события приближается к некоторому постоянному числу. Это явление называют статистической устойчивостью, а указанное число - статистической вероятностью события.
Результат каждого бросания монеты является случайным событием и непредсказуем. Однако явление статистической устойчивости гарантирует, что с увеличением числа повторений опыта частота события стремится к его вероятности.
Отметим, что статистическая вероятность позволяет определять фундаментальные математические постоянные, например, число π.