Плоская система произвольно расположенных сил

Теорема Пуансо
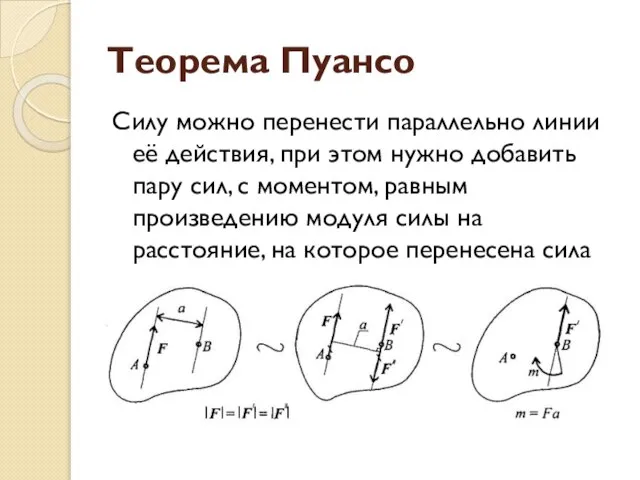
Силу можно перенести параллельно линии её действия, при этом нужно добавить пару сил, с моментом, равным произведению модуля силы на расстояние, на которое перенесена сила

Луи Пуансо
1777 − 1859
Французский математик и механик
Академик Парижской Академии наук
Ввёл понятие реакции связей, сформулировал принцип освобождаемости от связей

Произвольная плоская система сил ⇒
Силы не пересекаются в одной точке ⇒
Упрощаем, перенеся все силы системы в одну произвольную точку приведения ⇒
Применяем теорему Пуансо ⇒
При переносе силы в точку, не лежащую на линии действия, добавляем присоединённую пару сил

Произвольная плоская система сил
Точка приведения
Моменты
Главный вектор
Главный момент

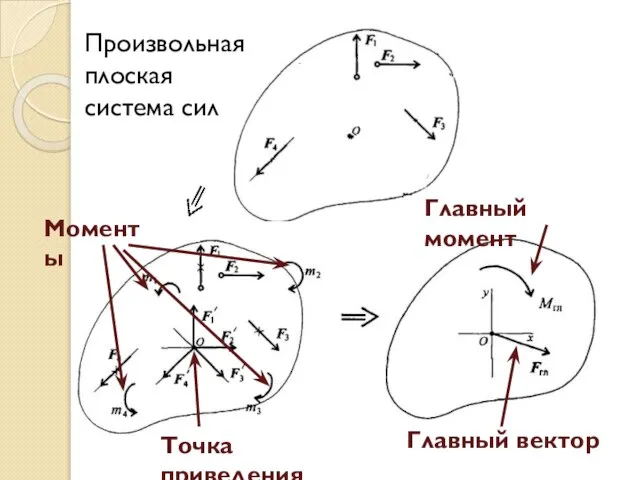
Главный вектор системы
Геометрическая сумма векторов
Для проекций
Модуль главного вектора

Главный момент системы
Алгебраическая сумма моментов сил системы относительно точки приведения

Условие равновесия
Для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы векторная сумма всех сил была равна нулю и алгебраическая сумма моментов всех сил относительно произвольно выбранной точки также была равна нулю

Основная форма уравнения равновесия

Уравнений моментов можно записать бесконечное множество
Но на плоскости можно составить только 3 независимых уравнения моментов, при этом центры моментов не должны лежать на одной линии
Для разных случаев − три группы уравнений равновесия

Формы уравнений равновесия
Первая
Вторая
Третья

Задача
Найти момент присоединённой пары при переносе силы F3 в точку В
F1=10 кН
F2=15 кН
F3=18 кН
a=0.2 м
По теореме Пуансо

Задача
Найти главный вектор системы и главный момент системы относительно точки В
F1=10 кН
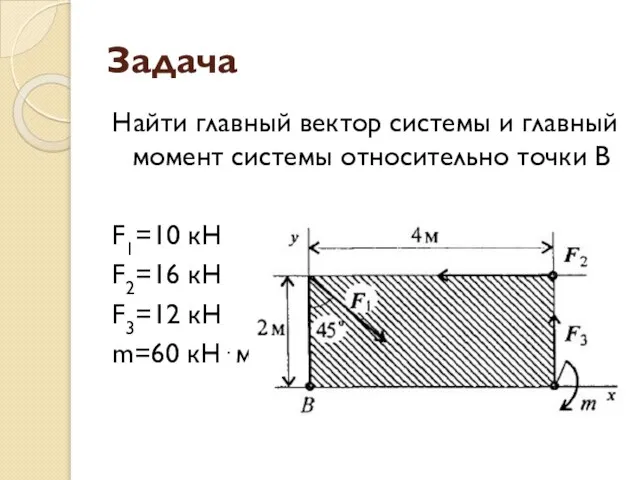
F2=16 кН
F3=12 кН
m=60 кН⋅м

Решение