Содержание
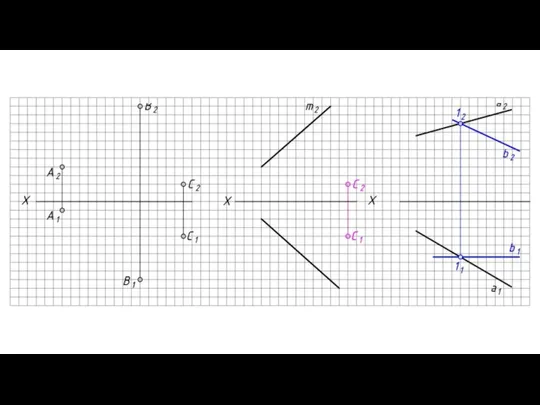
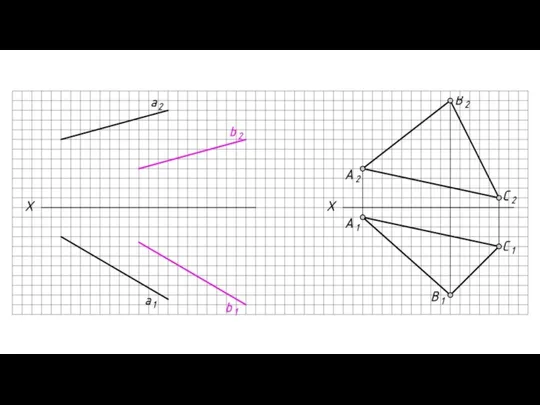
- 2. ЗАДАНИЕ ПЛОСКОСТИ НА ЧЕРТЕЖЕ Определителем плоскости являются три точки, не принадлежащие одной прямой. Для задания плоскости
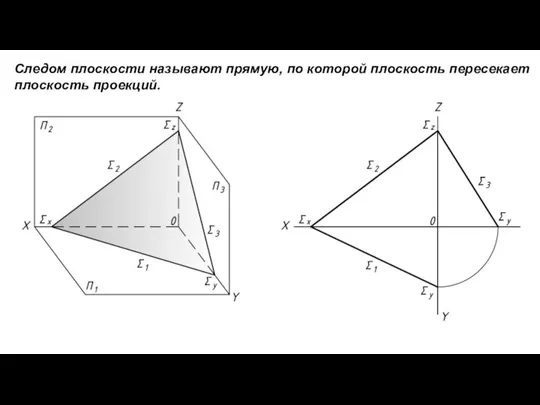
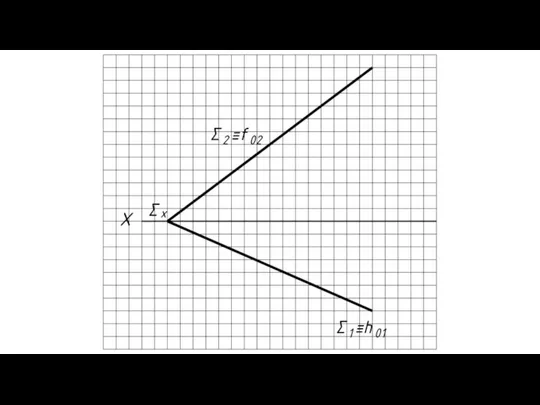
- 5. Следом плоскости называют прямую, по которой плоскость пересекает плоскость проекций.
- 6. КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ Плоскости общего положения – занимает произвольное положение по отношению к плоскостям проекций. Плоскости частного
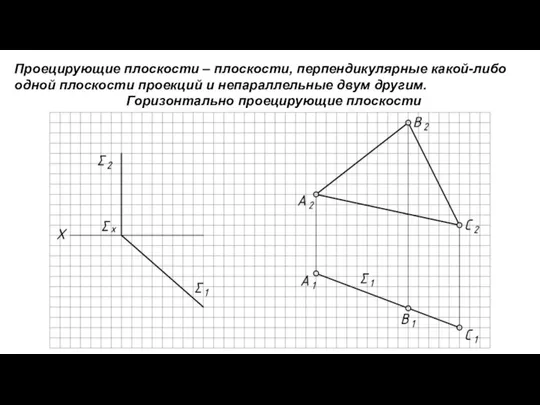
- 7. Проецирующие плоскости – плоскости, перпендикулярные какой-либо одной плоскости проекций и непараллельные двум другим. Горизонтально проецирующие плоскости
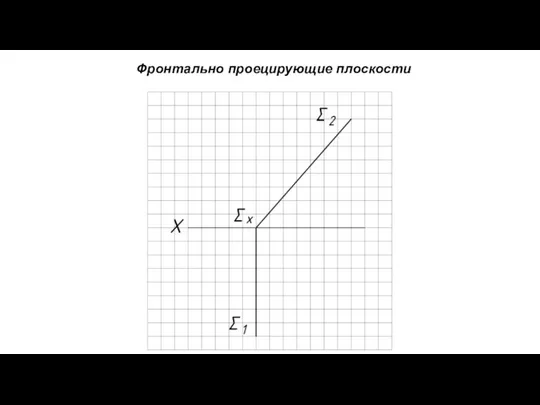
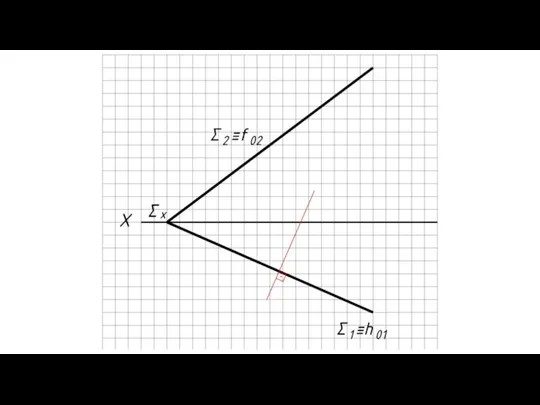
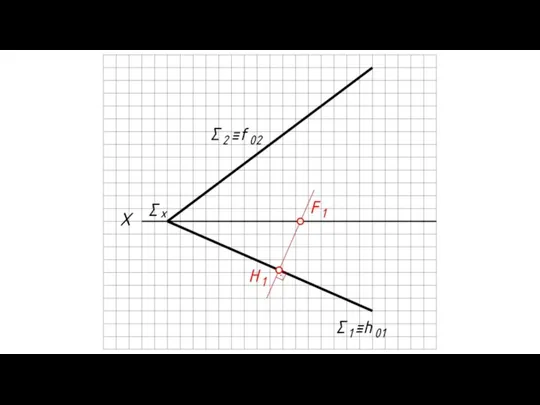
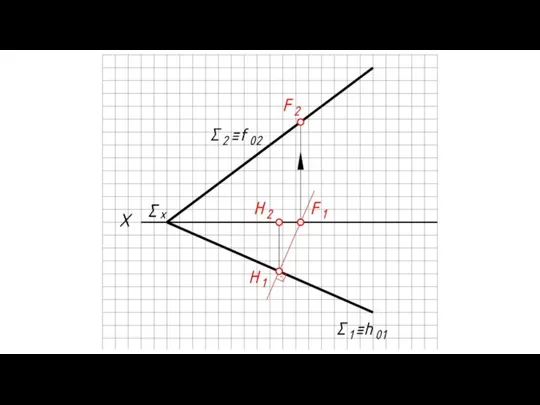
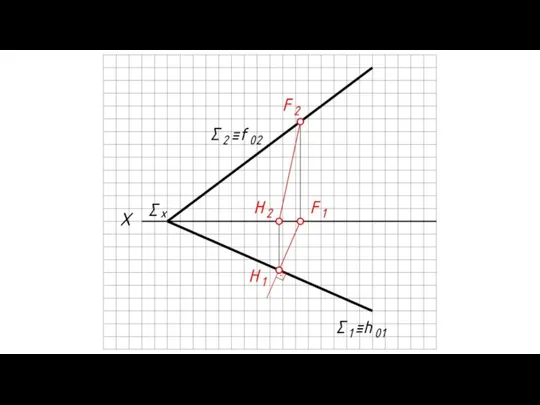
- 8. Фронтально проецирующие плоскости
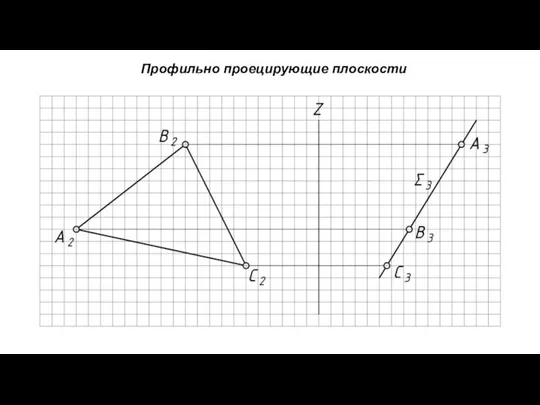
- 9. Профильно проецирующие плоскости
- 10. Плоскости уровня – плоскости, параллельные одной плоскости проекций и перпендикулярные двум другим плоскостям проекций. Плоскости горизонтального
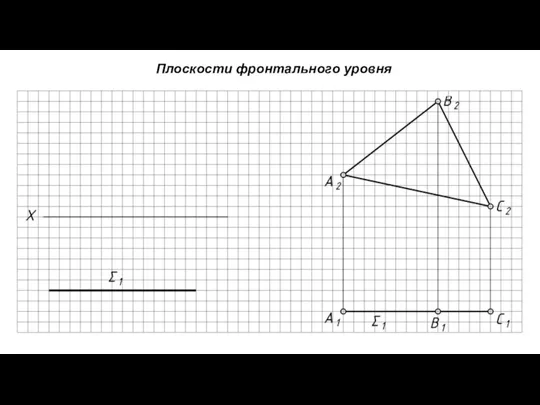
- 11. Плоскости фронтального уровня
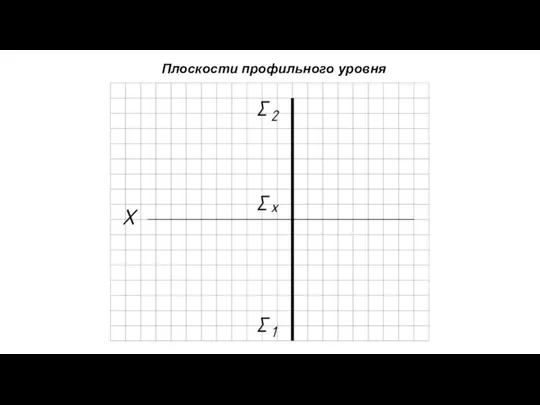
- 12. Плоскости профильного уровня
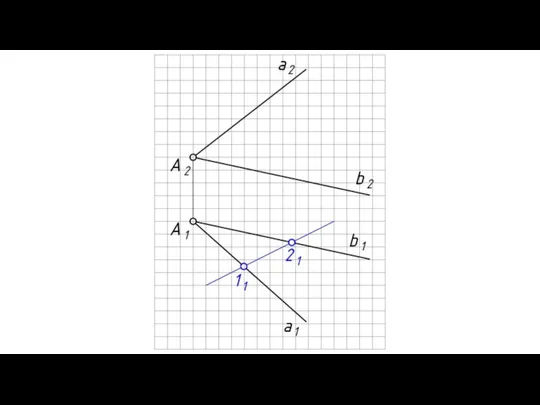
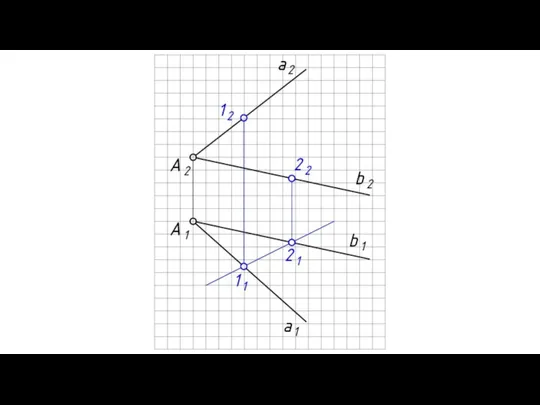
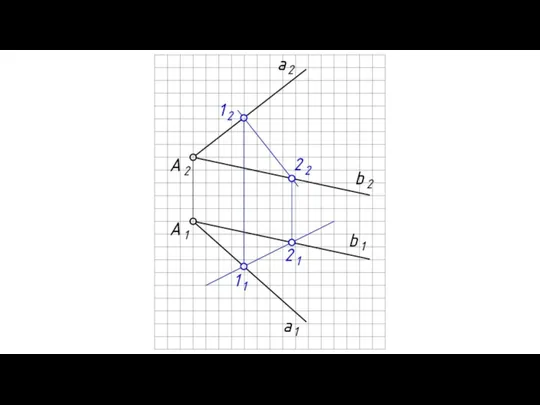
- 13. ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ ПЛОСКОСТИ Теорема: Прямая принадлежит плоскости, если она проходит через две точки принадлежащие
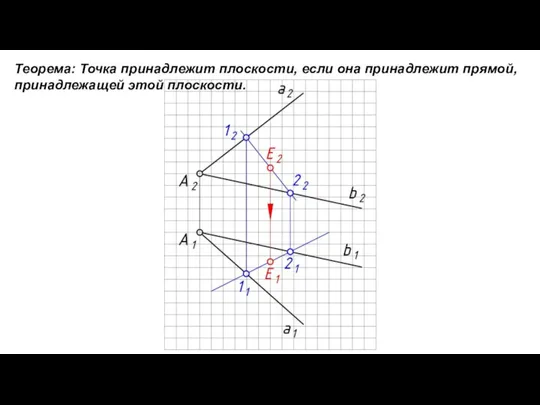
- 17. Теорема: Точка принадлежит плоскости, если она принадлежит прямой, принадлежащей этой плоскости.
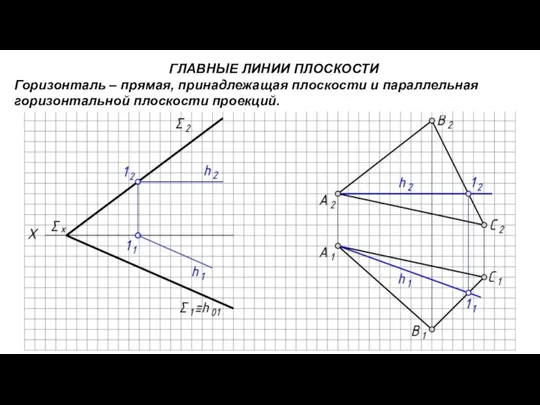
- 18. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ Горизонталь – прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций.
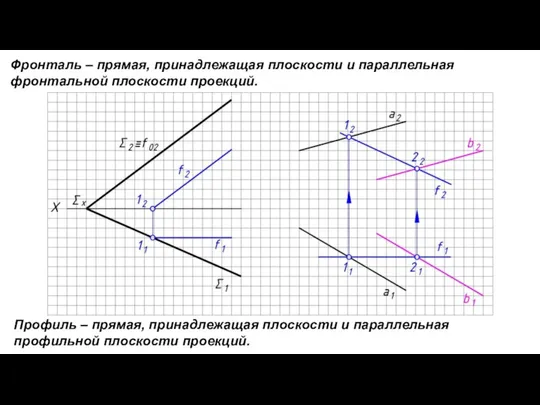
- 19. Фронталь – прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций. Профиль – прямая, принадлежащая плоскости и
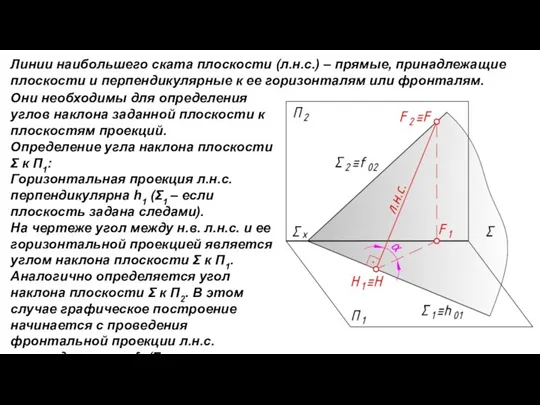
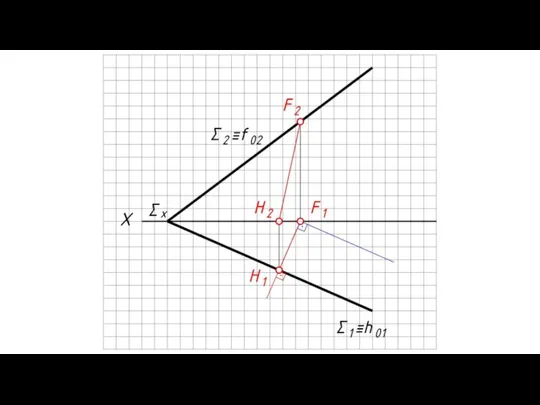
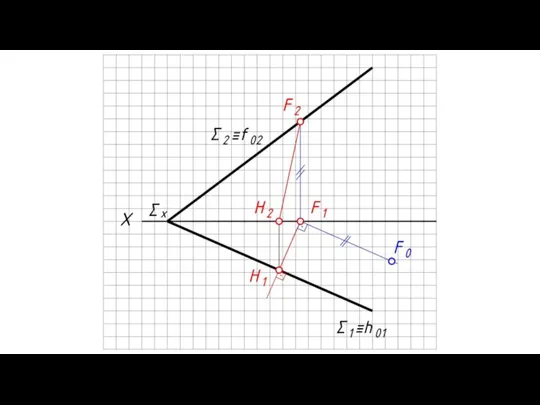
- 20. Линии наибольшего ската плоскости (л.н.с.) – прямые, принадлежащие плоскости и перпендикулярные к ее горизонталям или фронталям.
- 29. Скачать презентацию




 Программа “43 секунды”
Программа “43 секунды” Эстафета пионерских поколений
Эстафета пионерских поколений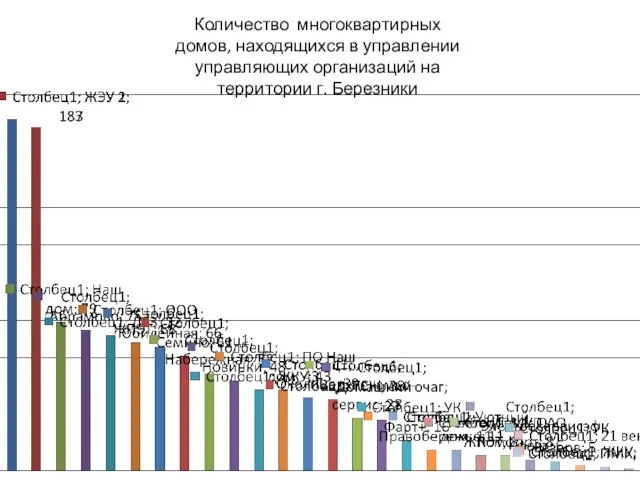 Количество многоквартирных домов, находящихся в управлении управляющих организаций на территории г. Березники
Количество многоквартирных домов, находящихся в управлении управляющих организаций на территории г. Березники Working with Directives and Pipes Presentation. Part 2
Working with Directives and Pipes Presentation. Part 2 Рим – открытый город
Рим – открытый город Основы автоматики
Основы автоматики НАНОТЕХНОЛОГИЧЕСКАЯ ПРОДУКЦИЯ И СПЕЦИАЛИЗИРОВАННОЕ ОБОРУДОВАНИЕ
НАНОТЕХНОЛОГИЧЕСКАЯ ПРОДУКЦИЯ И СПЕЦИАЛИЗИРОВАННОЕ ОБОРУДОВАНИЕ Презентация на тему Вавилов Николай Иванович
Презентация на тему Вавилов Николай Иванович Древний Рим / Римская империя. История искусства. Часть 2
Древний Рим / Римская империя. История искусства. Часть 2 Управление и менеджмент
Управление и менеджмент Правописание приставок в заданиях
Правописание приставок в заданиях 20141007_issledovatelskaya_deyatelnost
20141007_issledovatelskaya_deyatelnost Интернет
Интернет Интерактивно-аналитический онлайн-сервис Калькулятор процедур
Интерактивно-аналитический онлайн-сервис Калькулятор процедур Медиация. Никифорова Анастасия Владимировна. Контактная информация
Медиация. Никифорова Анастасия Владимировна. Контактная информация Проблемы формирования профессиональной компетентости специалистов в области организации дистанционного обучения
Проблемы формирования профессиональной компетентости специалистов в области организации дистанционного обучения Умножение чисел, оканчивающихся нулями
Умножение чисел, оканчивающихся нулями Результаты пробного ГИА-9 по русскому языку
Результаты пробного ГИА-9 по русскому языку Песколовки
Песколовки Однажды в ДКП
Однажды в ДКП СКОРОВАРКА SCARLETT SL-1529
СКОРОВАРКА SCARLETT SL-1529 Система
Система Развитие транспортной системы города Москвы
Развитие транспортной системы города Москвы Презентация на тему Числовые и буквенные выражения
Презентация на тему Числовые и буквенные выражения Финансовое обеспечение деятельности учреждения.Cубсидия на выполнение государственного (муниципального) задания. Субсидии на ин
Финансовое обеспечение деятельности учреждения.Cубсидия на выполнение государственного (муниципального) задания. Субсидии на ин Мобильный офис глазами пентестера Дмитрий Евтеев (Positive Technologies)
Мобильный офис глазами пентестера Дмитрий Евтеев (Positive Technologies) Суслики
Суслики Великие композиторы мира
Великие композиторы мира