Плоскость на эпюре Монжа

Способы задание плоскости
на эпюре

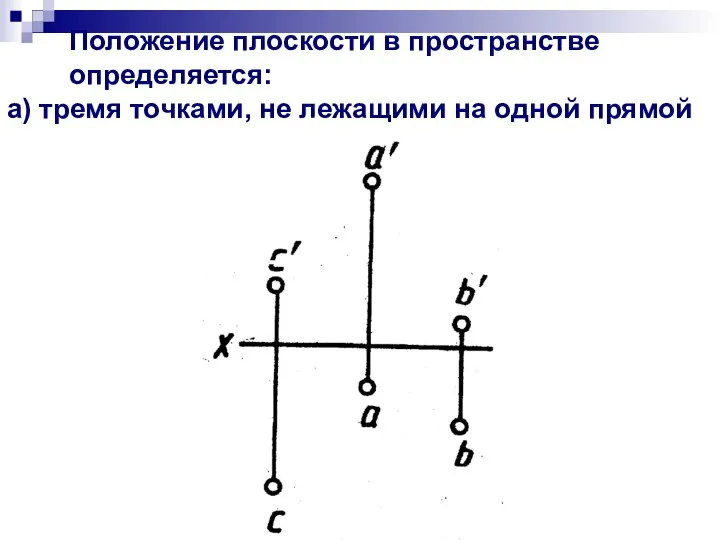
Положение плоскости в пространстве
определяется:
а) тремя точками, не лежащими на одной прямой

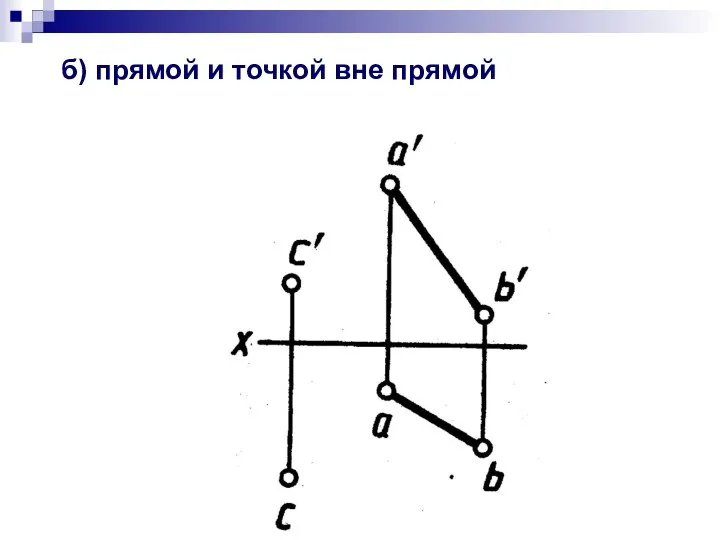
б) прямой и точкой вне прямой

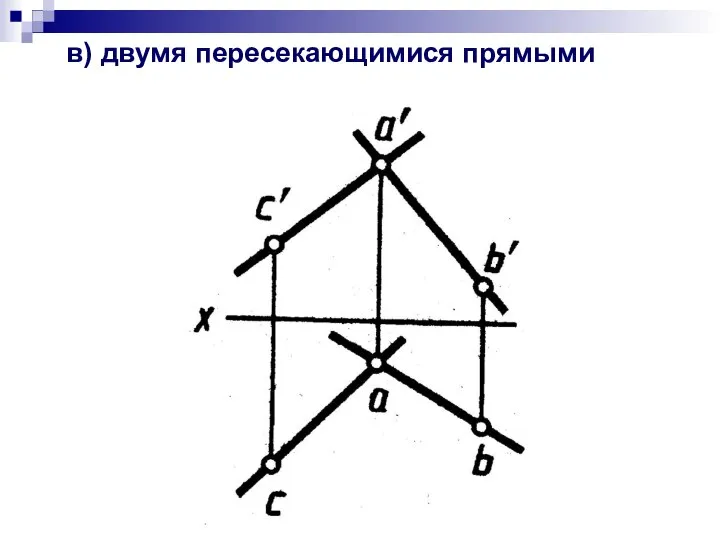
в) двумя пересекающимися прямыми

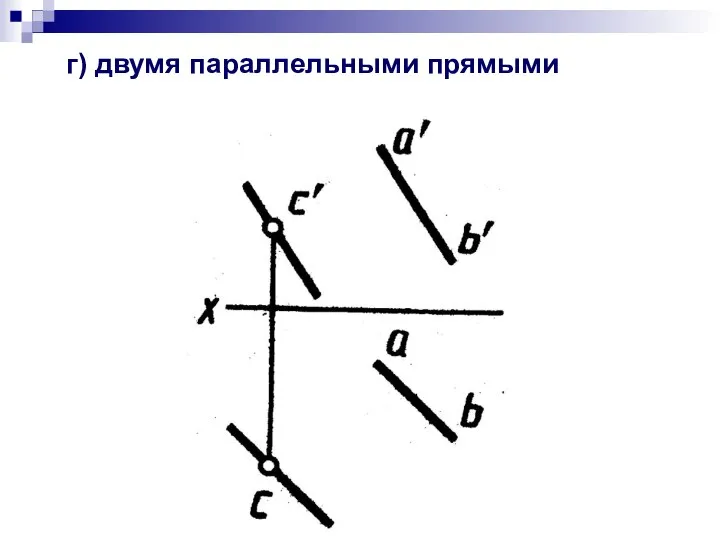
г) двумя параллельными прямыми

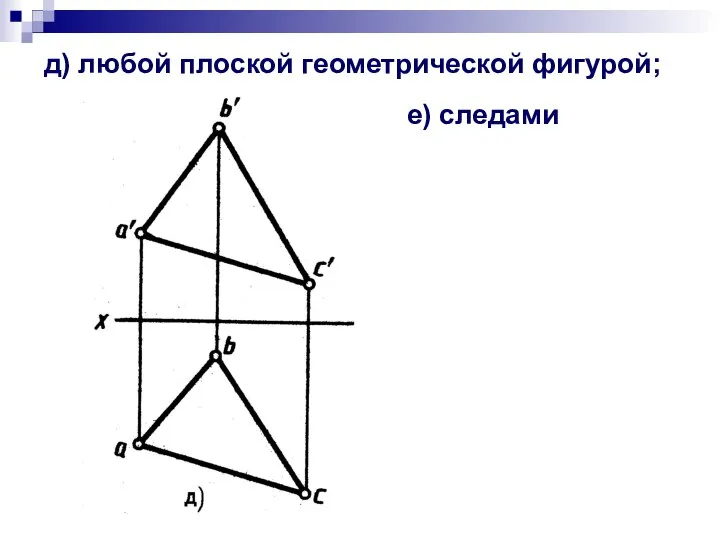
д) любой плоской геометрической фигурой;
е) следами

Положение плоскости относительно плоскостей проекций
В зависимости от положения плоскости относительно плоскостей проекций заданная плоскость может занимать общее или частное положение.

Плоскости общего положения не параллельны и не перпендикулярны ни к одной из плоскостей проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня.
Плоскости, перпендикулярные к какой-либо плоскости проекций, называются проецирующими.

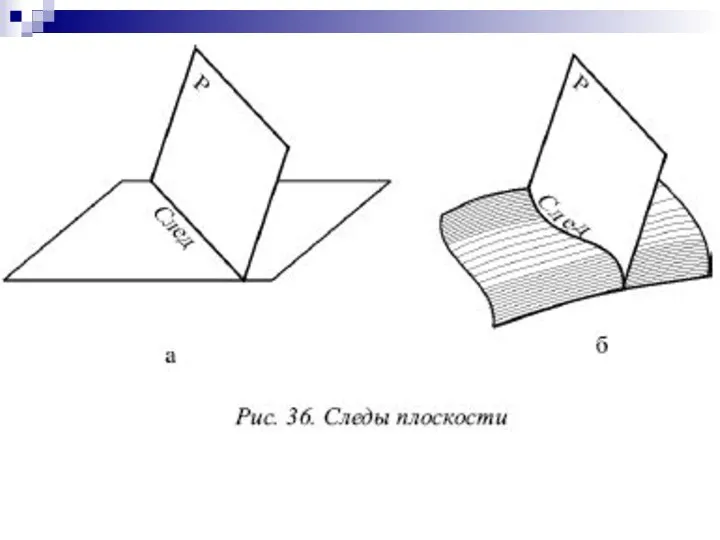
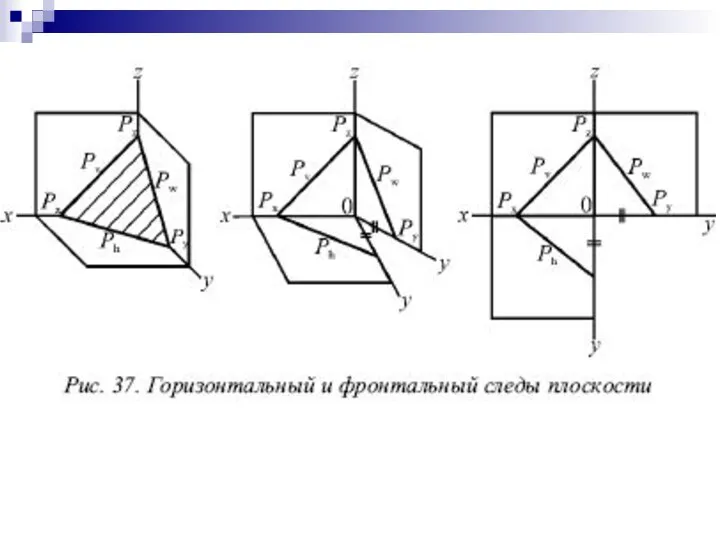
Линию пересечения плоскости с плоскостью проекций называют следом плоскости. Плоскости частного положения как правило задаются следами.
Следы плоскости

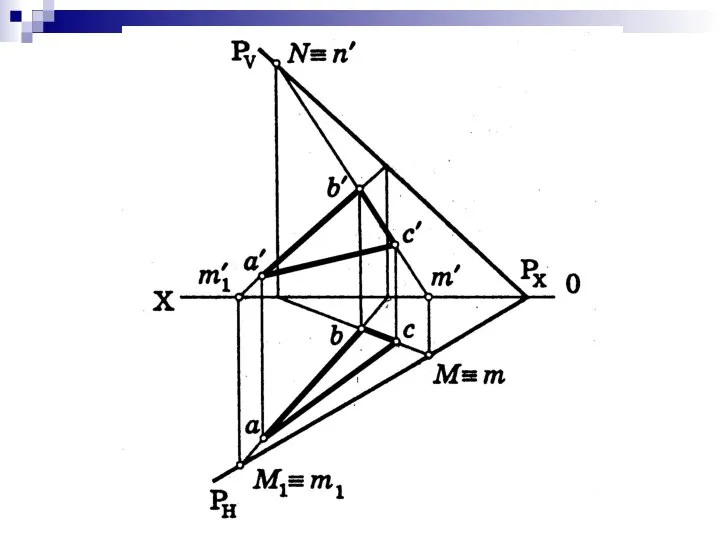
Построение следов плоскости
Для построения следов плоскости, заданной тремя точками, необходимо:
продолжить стороны треугольника, полученного соединением трех точек, и построить их следы;
соединить проекции пары следов на каждой плоскости проекций и получить следы заданной плоскости, которые имеют общую точку схода (точку пересечения) на оси проекций .

Прямая принадлежит плоскости, если она проходит через две точки этой плоскости (или через одну точку этой плоскости и параллельна прямой, лежащей в этой плоскости).
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Точка и прямая в плоскости

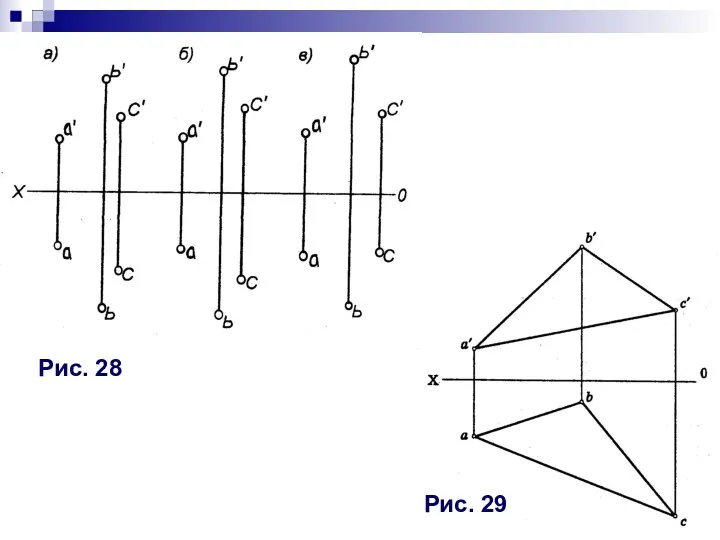
Домашнее задание
1. Плоскость, заданную тремя точками, изобразить (рис. 28):
а) двумя параллельными прямыми;
б) двумя пересекающимися прямыми;
в) плоской фигурой.
Координаты точек: А (50, 20, 20); В (30, 40, 40); С (20, 30, 30).
2. Построить следы плоскости Pv и PH, заданной треугольником АВС (рис. 29): А (70, 20, 10); В (35, 5, 40); С (5, 40, 20).
Построить следы плоскости Qv и QH, заданной треугольником DEF: D (50, 20, 10); E (30, 5, 15); F (20, 10, 5).

Рис. 28
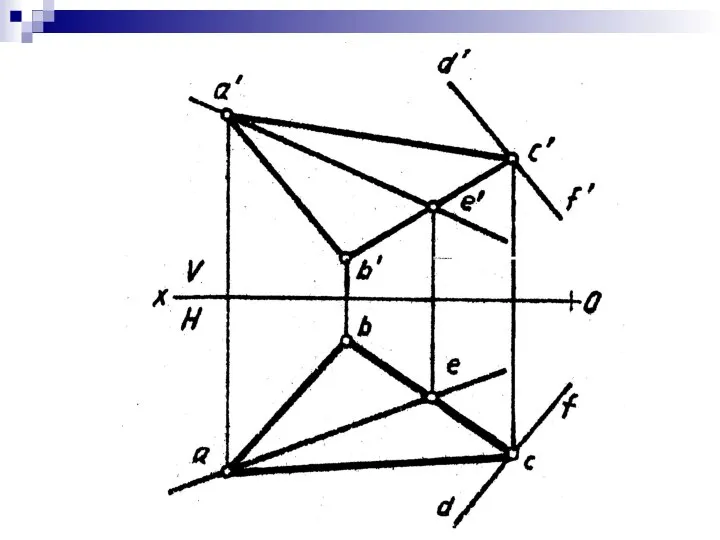
Рис. 29

3. По горизонтальной проекции фигуры KMLFE, принадлежащей плоскости параллелограмма: А(70,40,25); В(35,50,45);С(10,15,25);D(30,5,5), построить ее фронтальную проекцию (рис. 30).K(55,35); L(25,10); M(45,20); E(45,40); F(20,20).
*4. По фронтальной проекции плоской фигуры и горизонтальным проекциям двух ее смежных сторон достроить горизонтальную проекцию (рис. 31).
в 3-ем и 4-ом задании применить свойства принадлежности прямой плоскости и точки плоскости.
Задание выполнить на формате А3.