Сумма углов n угольника

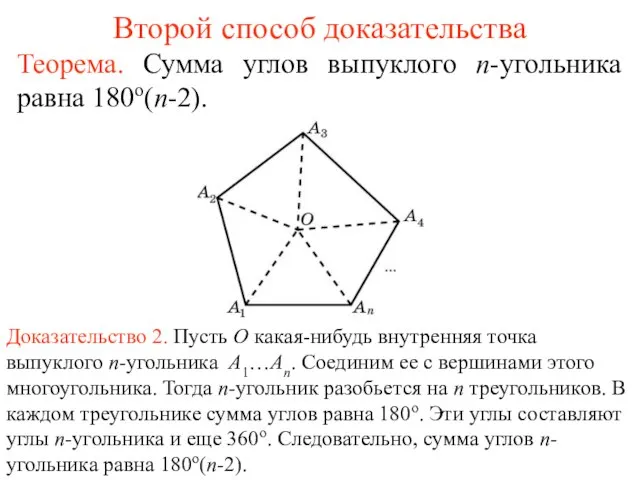
Второй способ доказательства
Теорема. Сумма углов выпуклого n-угольника равна 180o(n-2).
Доказательство 2. Пусть O какая-нибудь внутренняя точка выпуклого n-угольника A1…An. Соединим ее с вершинами этого многоугольника. Тогда n-угольник разобьется на n треугольников. В каждом треугольнике сумма углов равна 180о. Эти углы составляют углы n-угольника и еще 360о. Следовательно, сумма углов n-угольника равна 180о(n-2).

Упражнение 1
Чему равна сумма углов выпуклого: а) 4-угольника; б) 5-угольника; в) 6-угольника?
Ответ: а) 360о;
б) 540о;
в) 720о.

Упражнение 2
Чему равен внешний угол правильного: а) 3-угольника; б) 4-угольника; в) 5-угольника; г) 6-угольника?
Ответ: а) 120о;
б) 90о;
в) 72о;
г) 60о.

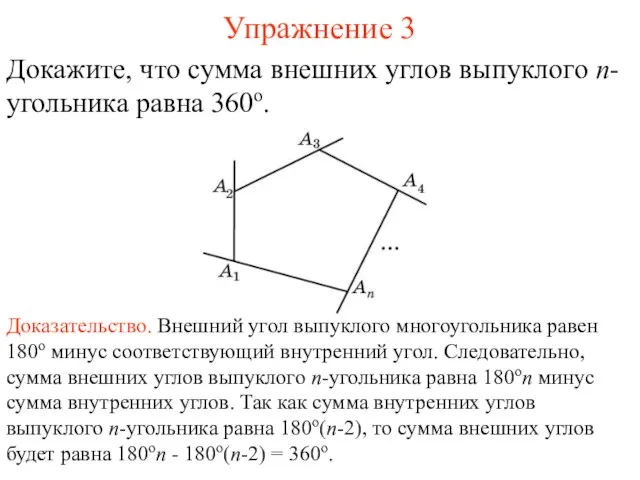
Упражнение 3
Докажите, что сумма внешних углов выпуклого n-угольника равна 360о.
Доказательство. Внешний угол выпуклого многоугольника равен 180о минус соответствующий внутренний угол. Следовательно, сумма внешних углов выпуклого n-угольника равна 180оn минус сумма внутренних углов. Так как сумма внутренних углов выпуклого n-угольника равна 180о(n-2), то сумма внешних углов будет равна 180оn - 180о(n-2) = 360о.

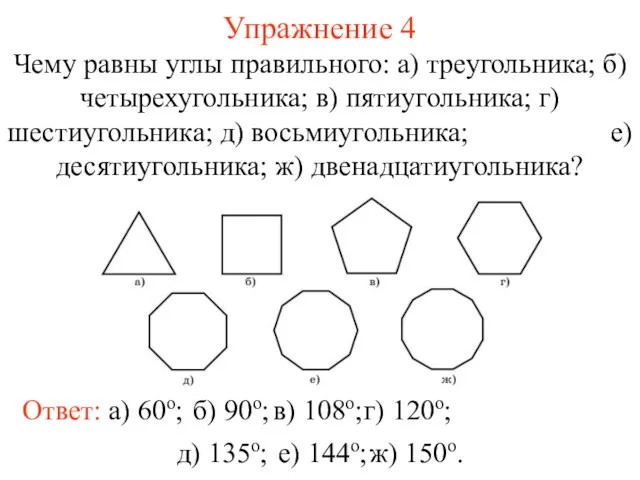
Упражнение 4
Чему равны углы правильного: а) треугольника; б) четырехугольника; в) пятиугольника; г) шестиугольника; д) восьмиугольника; е) десятиугольника; ж) двенадцатиугольника?
Ответ: а) 60о;
б) 90о;
в) 108о;
г) 120о;
д) 135о;
е) 144о;
ж) 150о.

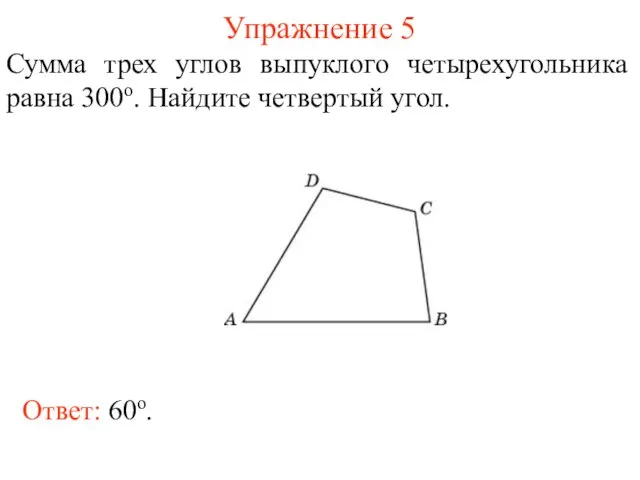
Упражнение 5
Сумма трех углов выпуклого четырехугольника равна 300о. Найдите четвертый угол.
Ответ: 60о.

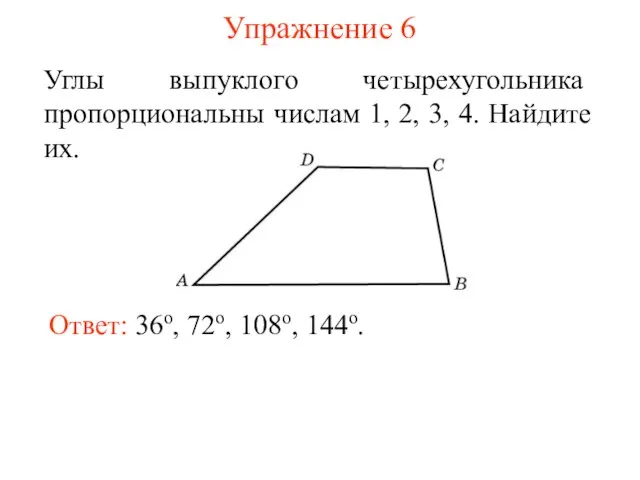
Упражнение 6
Углы выпуклого четырехугольника пропорциональны числам 1, 2, 3, 4. Найдите их.
Ответ: 36о, 72о, 108o, 144o.

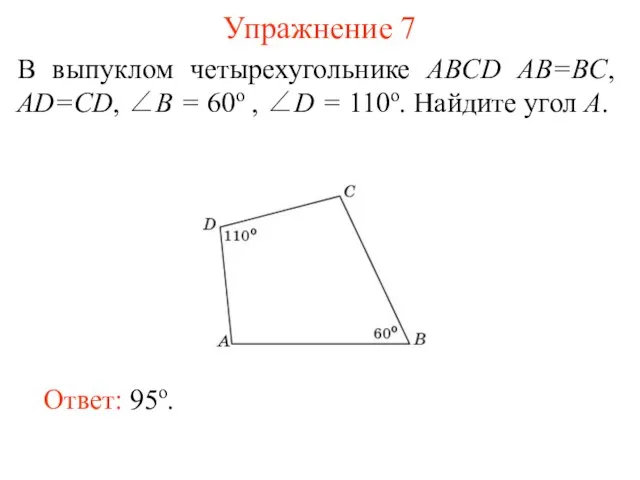
Упражнение 7
В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B = 60о , ∠D = 110о. Найдите угол A.
Ответ: 95о.

Упражнение 8
Сумма углов выпуклого многоугольника равна 900o. Сколько у него сторон?
Ответ: 7.

Упражнение 9
Сколько сторон имеет правильный многоугольник, если каждый из его внешних углов равен: а) 36o; б) 24o?
Ответ: а) 10;
б) 15.

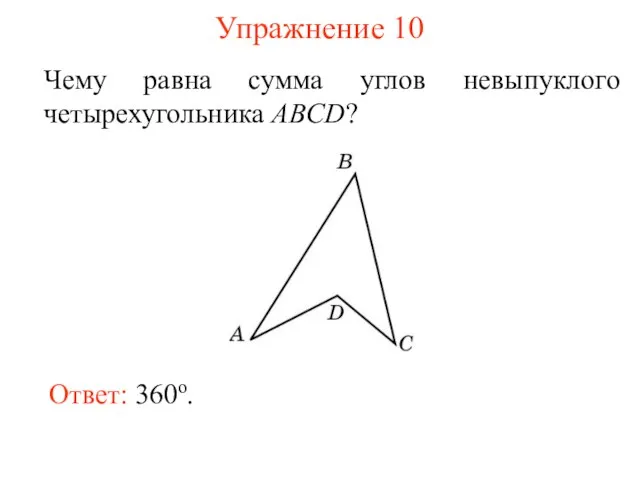
Упражнение 10
Чему равна сумма углов невыпуклого четырехугольника ABCD?
Ответ: 360о.

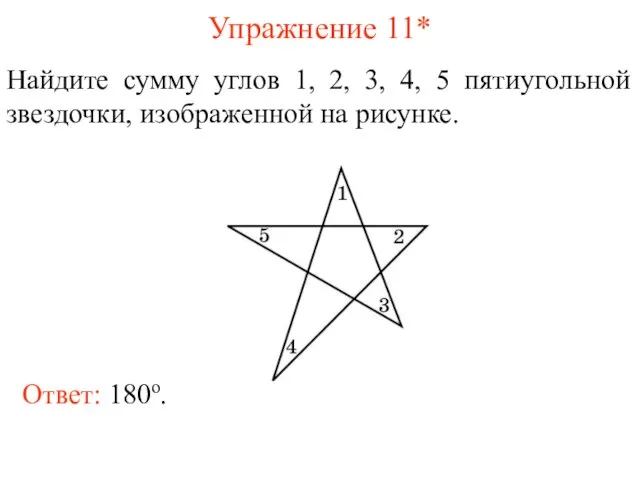
Упражнение 11*
Найдите сумму углов 1, 2, 3, 4, 5 пятиугольной звездочки, изображенной на рисунке.
Ответ: 180о.