Подготовка к ЕГЭ.

Задачи по геометрии
в пробных вариантах ЕГЭ

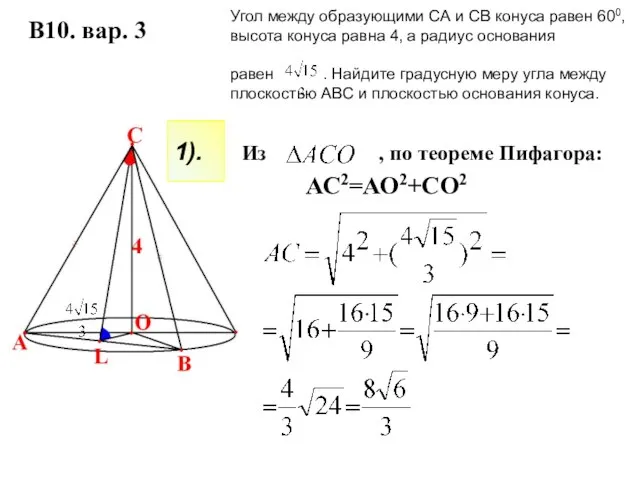
Из , по теореме Пифагора:
Угол между образующими СА и СВ конуса равен 600, высота конуса равна 4, а радиус основания
равен . Найдите градусную меру угла между плоскостью АВС и плоскостью основания конуса.
В10. вар. 3
АС2=АО2+СО2
1).

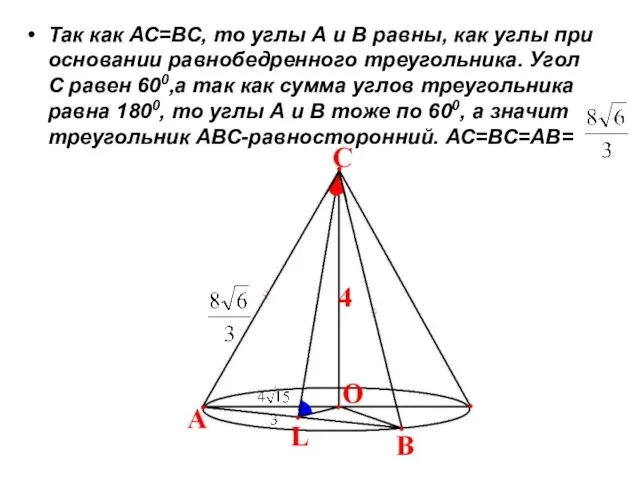
Так как АС=ВС, то углы А и В равны, как углы при основании равнобедренного треугольника. Угол С равен 600,а так как сумма углов треугольника равна 1800, то углы А и В тоже по 600, а значит треугольник АВС-равносторонний. АС=ВС=АВ=

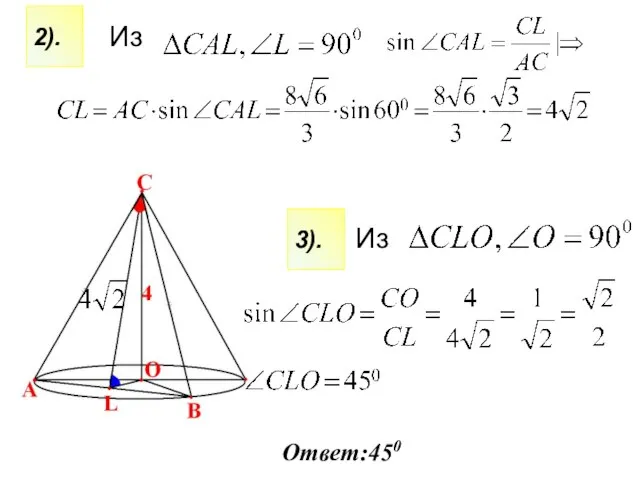
Из
Из
2).
3).
Ответ:450

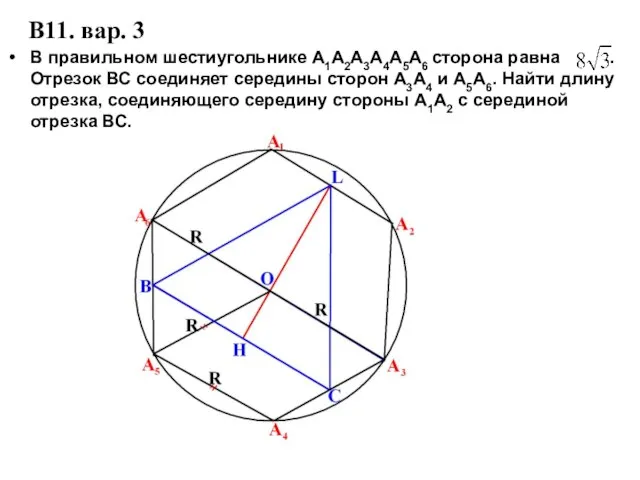
В11. вар. 3
В правильном шестиугольнике А1А2А3А4А5А6 сторона равна . Отрезок ВС соединяет середины сторон А3А4 и А5А6. Найти длину отрезка, соединяющего середину стороны А1А2 с серединой отрезка ВС.

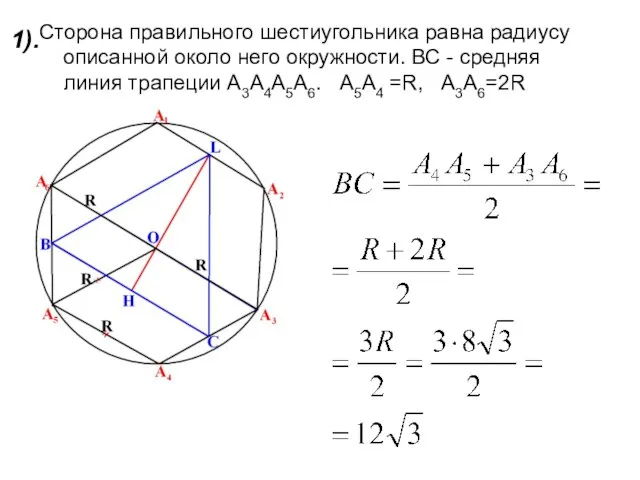
1).
Сторона правильного шестиугольника равна радиусу описанной около него окружности. ВС - средняя линия трапеции А3А4А5А6. А5А4 =R, А3А6=2R

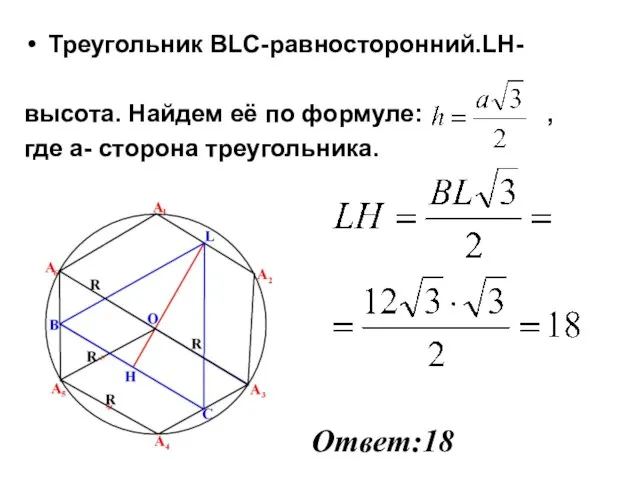
Треугольник BLC-равносторонний.LH-
высота. Найдем её по формуле: ,
где а- сторона треугольника.
Ответ:18

Площадь полной поверхности прямоугольного параллелепипеда можно вычислить по формуле:
S=2(ab+ac+bc)
Повторение

Уравнение плоскости в отрезках:
,
где a, b, c –абсцисса, ордината и аппликата
точек пересечения плоскости с осями
координат.
Повторение

Если Ax+By+Cz+D=0 -уравнение плоскости ά, то:
Повторение

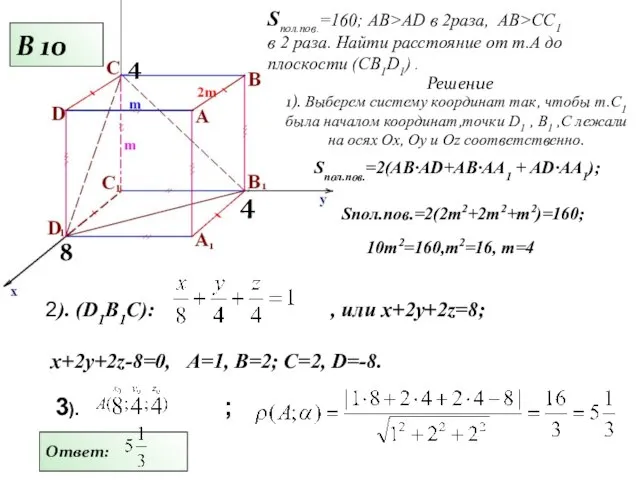
2). (D1B1C): , или x+2y+2z=8;
x+2y+2z-8=0, А=1, В=2; С=2, D=-8.
Sпол.пов.=160; АВ>AD в 2раза, AB>CC1
в 2 раза. Найти расстояние от т.А до плоскости (СВ1D1) .
Решение
Sпол.пов.=2(AB·AD+AB·AA1 + AD·AA1);
8
4
3). ;
Ответ:
B 10
Sпол.пов.=2(2m2+2m2+m2)=160;
10m2=160,m2=16, m=4
4
1). Выберем систему координат так, чтобы т.С1 была началом координат,точки D1 , B1 ,C лежали на осях Ох, Оу и Оz соответственно.

Если - острый угол, то
Некоторые тригонометрические тождества:
1.а).
Если - острый угол, то
б).
в).

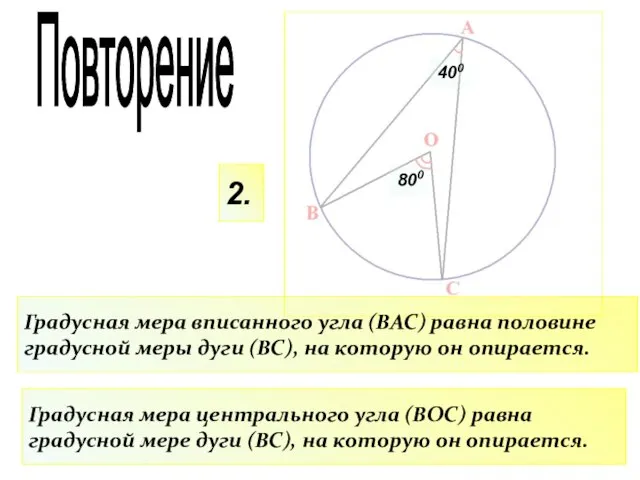
2.
Градусная мера вписанного угла (ВАС) равна половине градусной меры дуги (ВС), на которую он опирается.
Градусная мера центрального угла (ВОС) равна градусной мере дуги (ВС), на которую он опирается.
400
800
Повторение

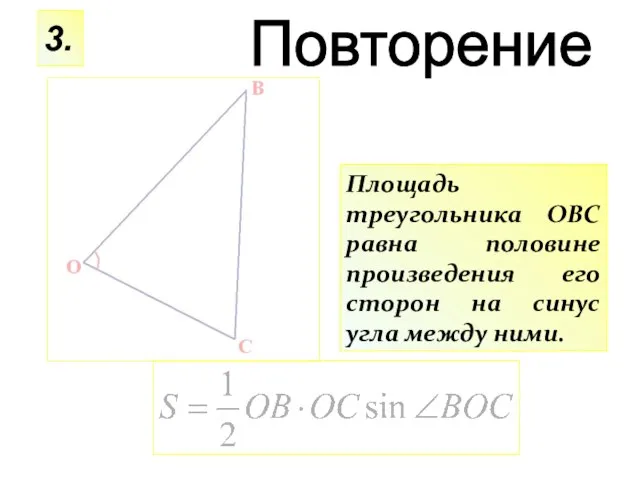
Площадь треугольника ОВС равна половине произведения его сторон на синус угла между ними.
3.
Повторение

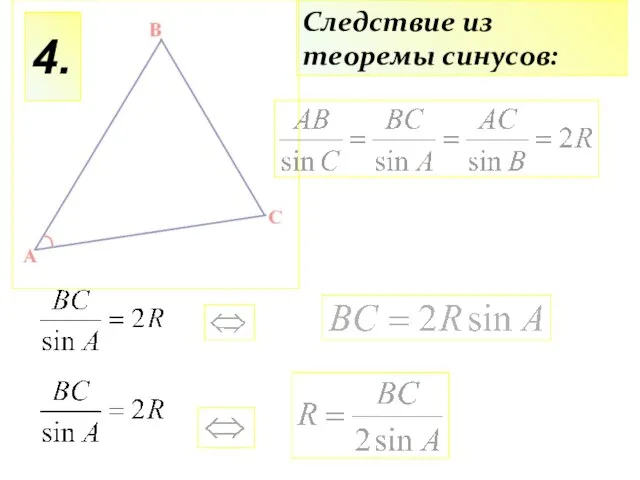
4.
Следствие из теоремы синусов:

В , ВС=12, ctgA=3. Найти где О-центр описанной около треугольника АВС окружности.
По следствию из теоремы синусов:
1).
B 11
Решение.
3).
,как вписанный угол.
-как центральный, следовательно:
2).
12

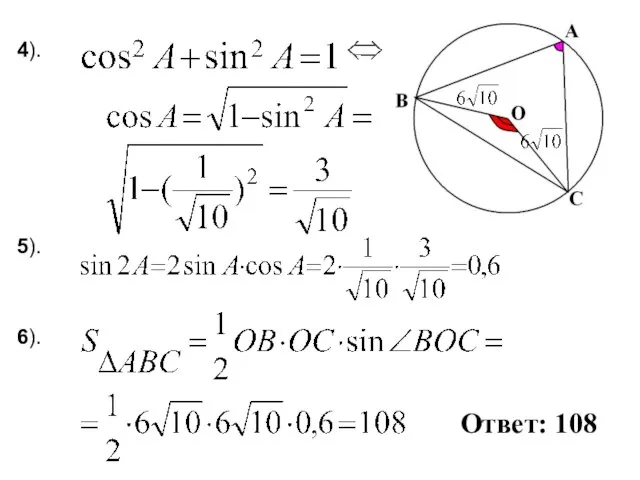
6).
5).
4).
Ответ: 108

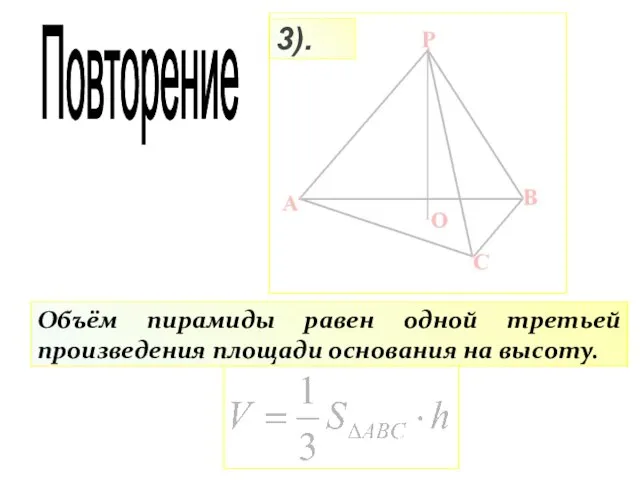
3).
Объём пирамиды равен одной третьей
произведения площади основания на высоту.
Повторение

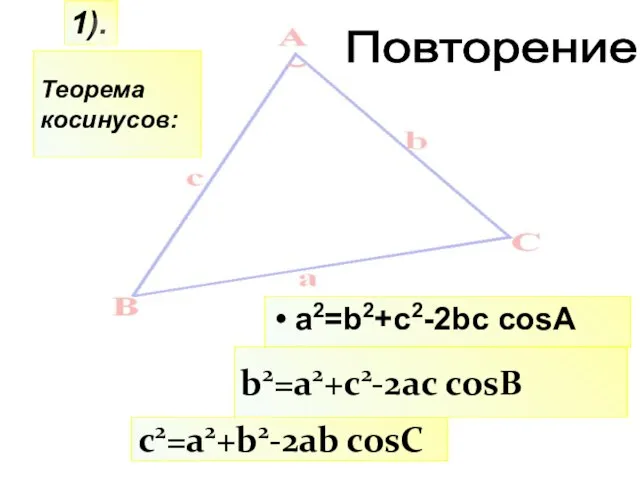
c2=a2+b2-2ab cosC
1).
b2=a2+c2-2ac cosB
Повторение
a2=b2+c2-2bc cosA
Теорема косинусов:

Теорема Пифагора:
«В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
c2=a2+b2
2).
Повторение

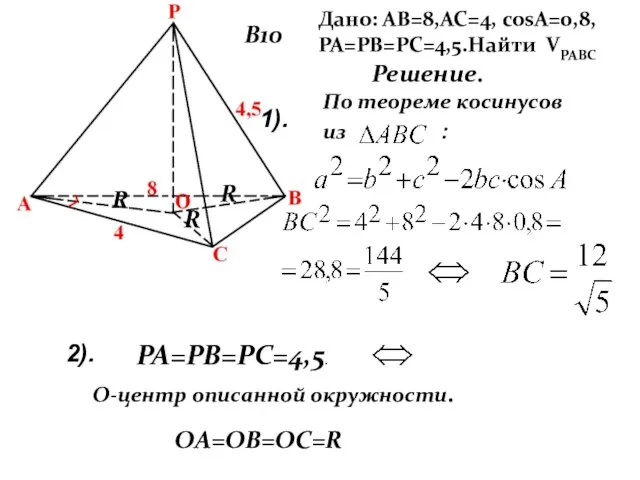
В10
Дано: АВ=8,АС=4, cosA=0,8, РА=РВ=РС=4,5.Найти VРАВС
Решение.
По теореме косинусов
из :
2).
1).
РА=РВ=РС=4,5.
OА=OВ=OС=R
O-центр описанной окружности.
R
R
R

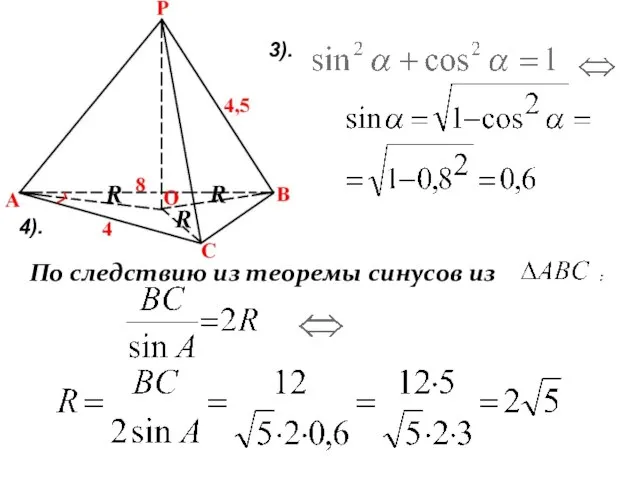
4).
По следствию из теоремы синусов из :
3).
R
R
R

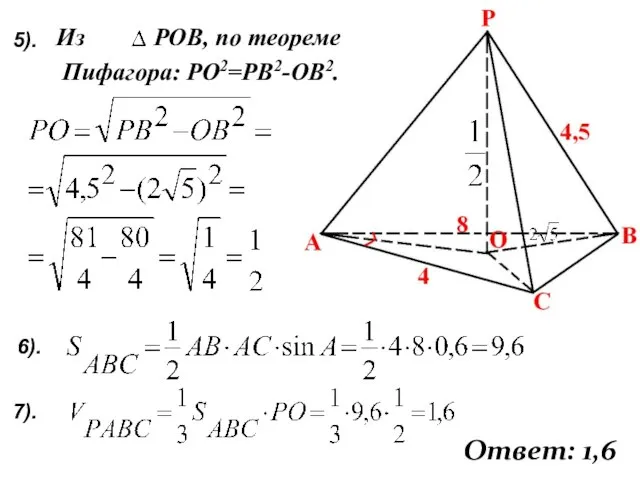
Из РОВ, по теореме
Пифагора: РО2=РВ2-ОВ2.
7).
Ответ: 1,6
5).
6).

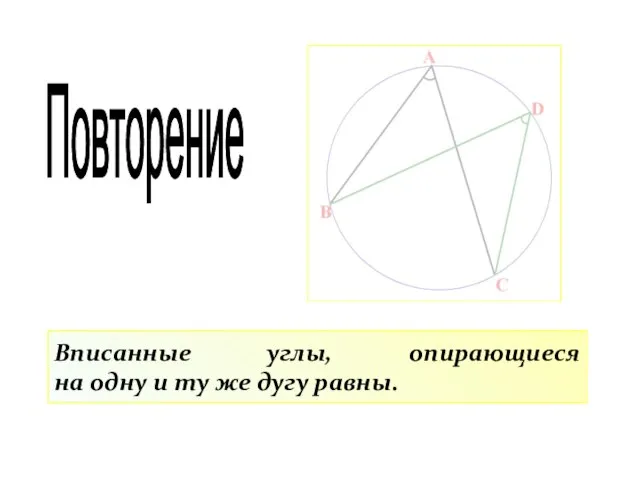
Вписанные углы, опирающиеся
на одну и ту же дугу равны.
Повторение

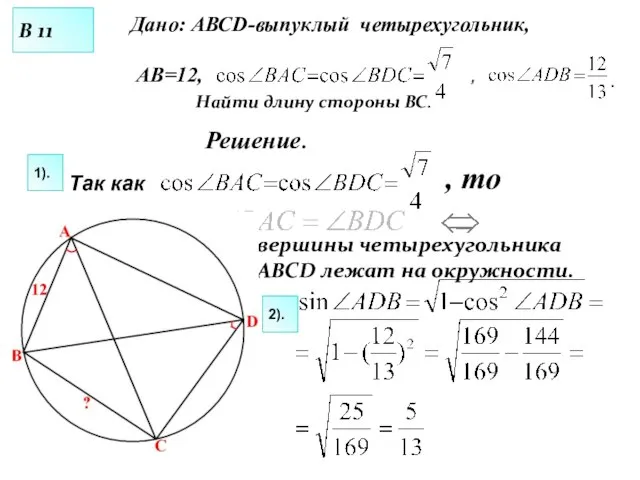
Дано: АВСD-выпуклый четырехугольник,
АВ=12, ,
, то
Найти длину стороны ВС.
Решение.
2).
1).
Так как
вершины четырехугольника ABCD лежат на окружности.
В 11
.

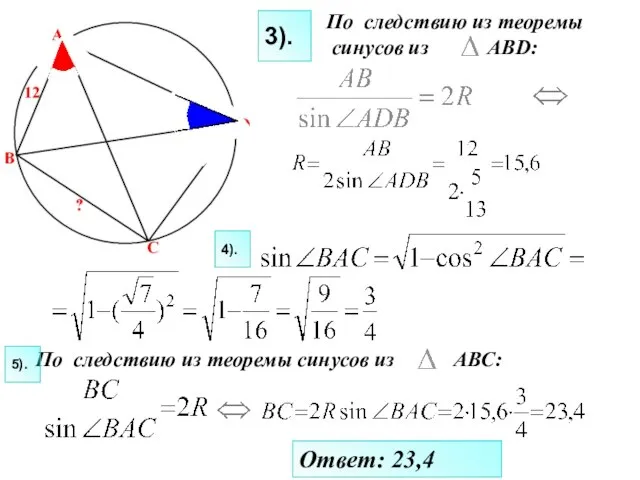
Ответ: 23,4
По следствию из теоремы синусов из АВС:
5).
4).
По следствию из теоремы
синусов из АВD:
3).

IIвариант.
Дано: ABCD-выпуклый четырехугольник, АВ=14. , . Найти длину стороны ВС. I вариант.
В , ВС=6, ctgA=3. Найти , где О- центр описанной около треугольника АВС окружности.
Самостоятельная
работа.