ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

Пропорциональные отрезки
Отношением отрезков AB и CD называется отношение их длин, т.е.
Отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1, если

Определение подобных треугольников
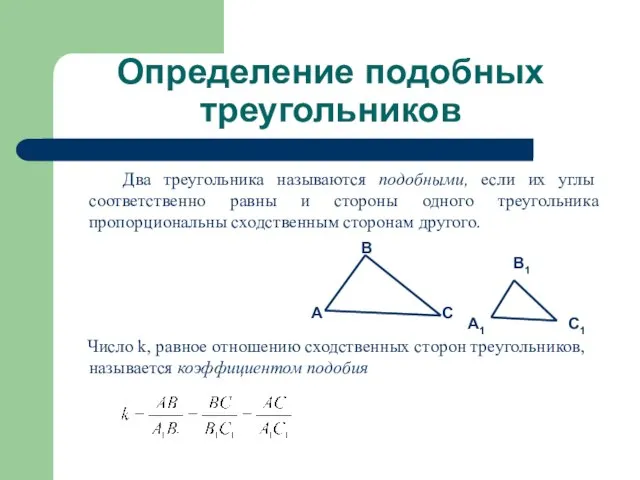
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия

Отношение площадей подобных треугольников
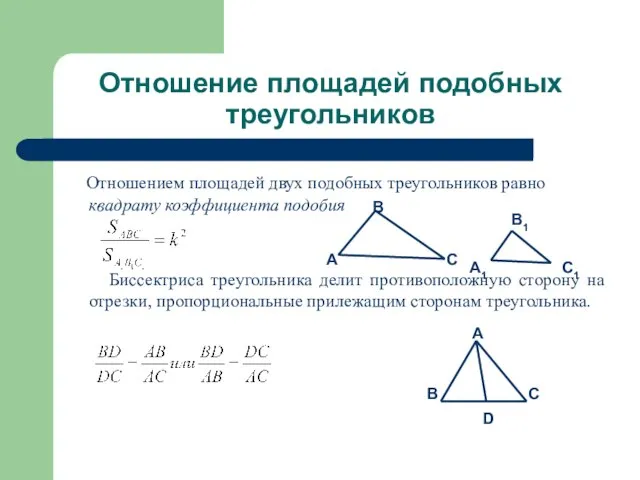
Отношением площадей двух подобных треугольников равно квадрату коэффициента подобия
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Признаки подобия треугольников
I признак подобия треугольников
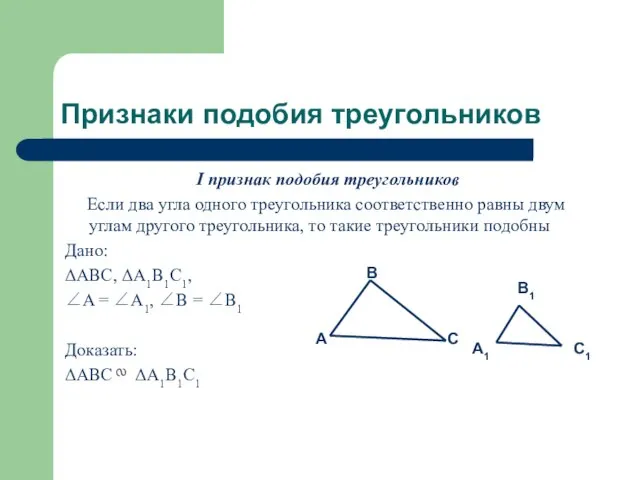
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны
Дано:
ΔABC, ΔA1B1C1,
∠A = ∠A1, ∠B = ∠B1
Доказать:
ΔABC ΔA1B1C1

Признаки подобия треугольников
II признак подобия треугольников
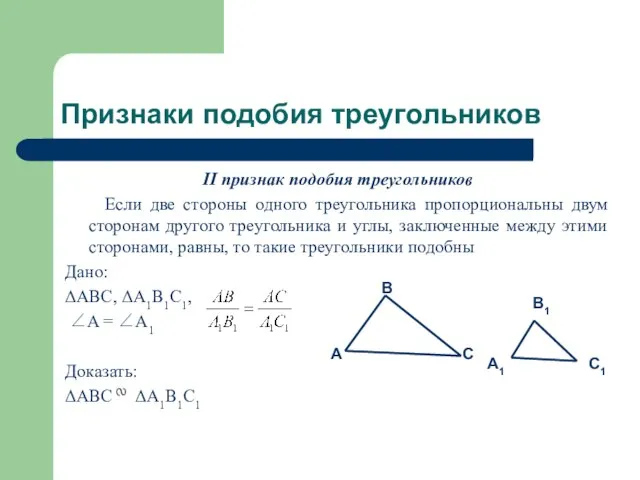
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
Дано:
ΔABC, ΔA1B1C1,
∠A = ∠A1
Доказать:
ΔABC ΔA1B1C1

Признаки подобия треугольников
III признак подобия треугольников
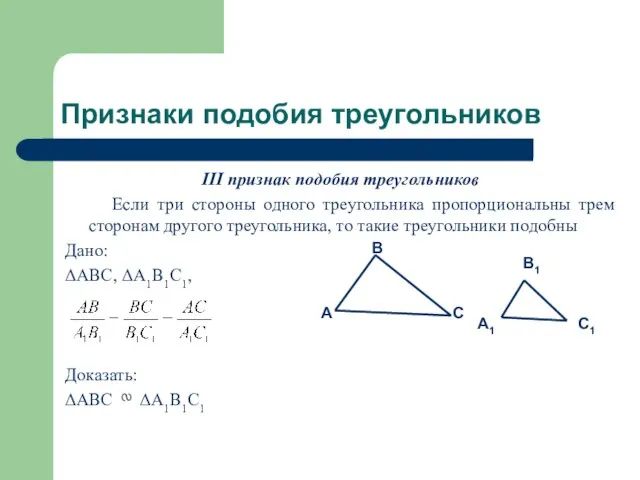
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
Дано:
ΔABC, ΔA1B1C1,
Доказать:
ΔABC ΔA1B1C1

Применение подобия к доказательству теорем
Средняя линия треугольника
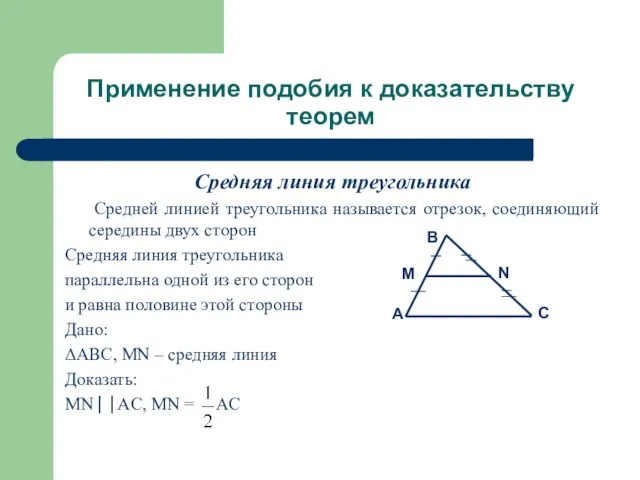
Средней линией треугольника называется отрезок, соединяющий середины двух сторон
Средняя линия треугольника
параллельна одной из его сторон
и равна половине этой стороны
Дано:
ΔABC, MN – средняя линия
Доказать:
MN⎮⎮AC, MN = AC

Применение подобия к решению задач
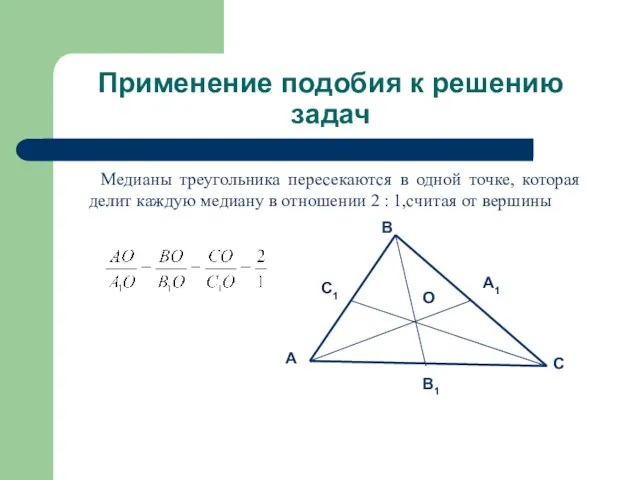
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1,считая от вершины

Применение подобия к решению задач
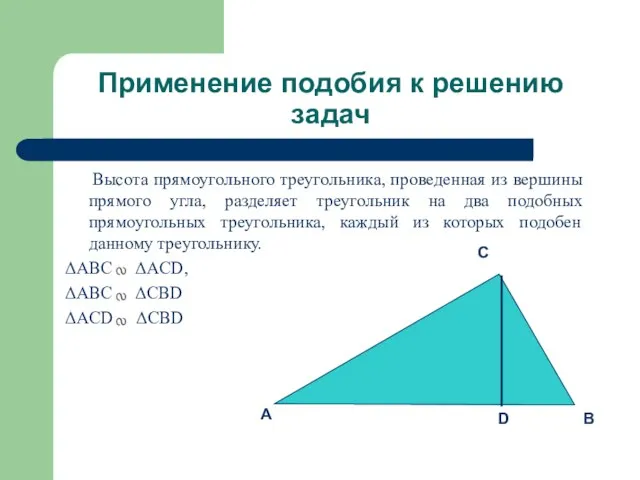
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
ΔABC ΔACD,
ΔABC ΔCBD
ΔACD ΔCBD

Применение подобия к доказательству теорем
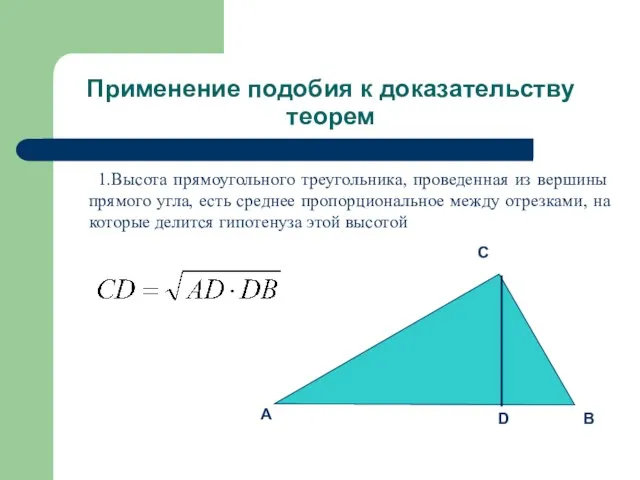
1.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой