Содержание
- 2. С развитием рыночных отношений ускорился процесс расслоения общества, обусловленный различием в доходах отдельных групп населения
- 3. Проблема справедливого распределения доходов стояла перед человечеством во все времена. И в настоящее время она не
- 4. Основная проблема настоящего времени в социальной сфере -неравенство в доходах между различными категориями граждан
- 5. Дифференциация доходов населения (домохозяйств) изучается в различных аспектах (по размеру семьи, по типу семей, по имущественному
- 6. На основании распределения населения по размеру среднедушевого дохода рассчитываются следующие абсолютные и относительные показатели дифференциации: модальное
- 7. медианное значение дохода Ме, средний доход , децильный коэффициент дифференциации Кd, коэффициент фондов Кф, коэффициент Джини
- 8. В расчете коэффициентов принимают участие либо величина доходов крайних групп населения (низко- и высокодоходных), либо распределение
- 9. Модальное значение Мo определяет наиболее распространенный среди населения уровень дохода. Медианный уровень Ме указывает, что одна
- 10. Коэффициенты дифференциации доходов населения Устанавливают размер превышения денежных доходов высокодоходных групп по сравнению с низкодоходными группами
- 11. Децильный коэффициент дифференциации – отношение уровней доходов, ниже и выше которых находятся по 10% совокупности в
- 12. Децильный коэффициент дифференциации доходов показывает, во сколько раз минимальный доход 10% самого богатого населения превышает максимальный
- 13. Кd = D9 : D1 где D9, D1 – соответственно девятый (верхний) и первый (нижний) децили,
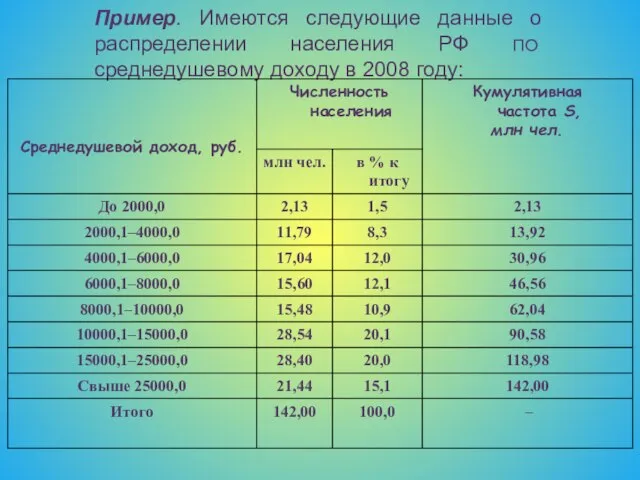
- 15. Пример. Имеются следующие данные о распределении населения РФ по среднедушевому доходу в 2008 году:
- 16. Рассчитаем модальный и медианный доходы:
- 18. По нашему примеру из графы накопленных частот следует, что значение нижнего дециля D1, соответствующего 1/10 суммы
- 20. Значение верхнего дециля находится в интервале 25–35 тыс. руб., так как 9/10 суммы частот составляет 127,8
- 21. т. е. Kd = 29,11 :4,03 = 7,2 раза
- 22. Следовательно, минимальный доход 10% самого богатого населения превышает в 7,2 раза максимальный доход 10% наименее обеспеченного
- 23. Коэффициент дифференциации фондов характеризует степень социального расслоения и определяется как отношение средних денежных доходов 10% населения
- 24. Коэффициент фондов
- 25. Так как знаменатели этих средних доходов одинаковы, то где Ф1, Ф10 – суммарный доход первой и
- 26. Так же измеряет соотношение между средними значениями доходов внутри сравниваемых групп населения или их долями в
- 27. Для нашего примера в группу наименьших доходов войдут первая (1,5%) и вторая группа (8,3%) и часть
- 28. Высокодоходную группу составят 10% из последней группы. Соответственно этим долям будет складываться суммарный доход:
- 29. Ф1 = 1⋅2,13 + 3⋅11,79 + 5⋅2,8 = =51,5 млрд руб.; Ф10 = 35⋅14,2= 497 млрд
- 30. Коэффициент фондов (соотношение доходов 10% наиболее и 10% наименее обеспеченного населения), коэффициент, январь-декабрь
- 31. Коэффициент фондов Несмотря на то, что для богатых мы взяли в качестве среднего дохода верхнюю границу
- 32. Для характеристики степени концентрации доходов вычисляется коэффициент Джини:
- 33. где k – число групп; Wнi – доля населения i-й группы с данным уровнем среднедушевого дохода;
- 34. Коэффициент Джини (индекс Джини) — статистический показатель, свидетельствующий о степени расслоения общества данной страны или региона
- 35. Пример По уровню годового дохода — наиболее частое применение, особенно при современных экономических расчетах
- 36. Рассчитывается как площадь области между кривой Лоренца, которая описывает реальное распределение, и идеальной прямой равномерного распределения
- 37. Максимально возможная площадь принимается за единицу измерения. Коэффициент Джини G может принимать значения от нуля до
- 38. G=0 означает равномерное распределение, G=1 — предельный случай, когда признаком обладает только один человек
- 39. Индекс Джини — коэффициент Джини, выраженный в процентах
- 40. Преимущества коэффициента Джини: Позволяет сравнивать распределение признака в совокупностях с различным числом единиц (например, регионы с
- 41. 4. Может быть использован для сравнения распределения признака (дохода) по разным группам населения (например, коэффициент Джини
- 42. Недостатки коэффициента Джини: Довольно часто коэффициент Джини приводится без описания группировки совокупности, то есть часто отсутствует
- 43. 3. Коэффициент Джини не учитывает источник дохода, то есть для определенной локации (страны, региона и т.
- 44. 4. Метод кривой Лоренца и коэффициента Джини в исследовании неравномерности распределения доходов среди населения имеет дело
- 45. Коэффициент Джини (0÷1), индекс Джини (0÷100 %)
- 46. Где, G G 0.25–0.29 G 0.30–0.34 G 0.35–0.39 G 0.40–0.44 G 0.45-0.49 G 0.50–0.54 G 0.55–0.59
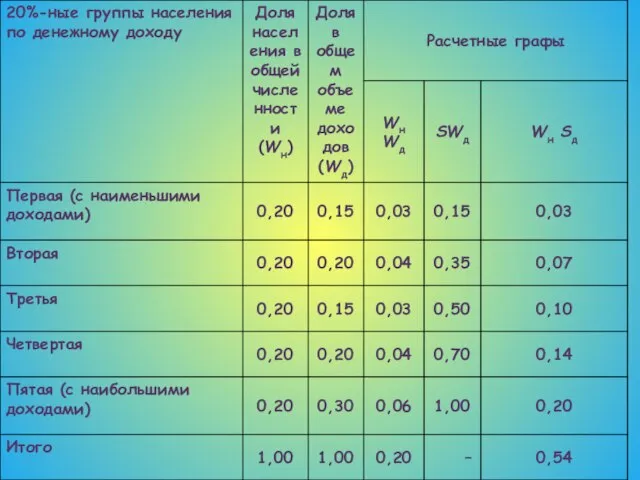
- 47. Пример. Вычислим КG по данным о распределении 20%-ных групп населения по общему объему денежных доходов:
- 49. КG = 1 – 2 ⋅ 0,54 + 0,20 = 0,28
- 50. Если учесть, что в базисном году коэффициент Джини составлял 0,19, то следует сделать вывод об усилении
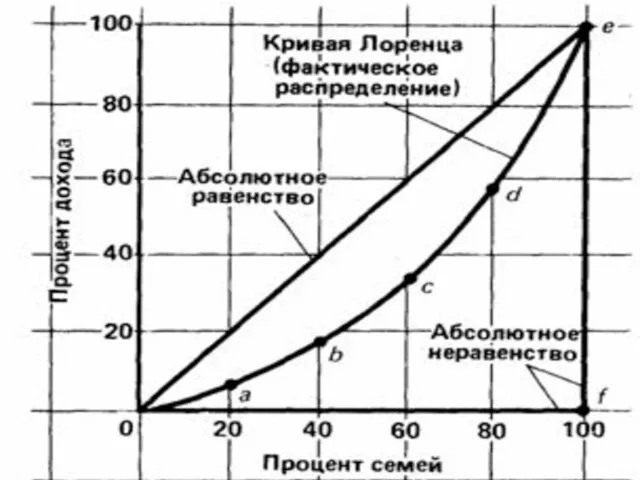
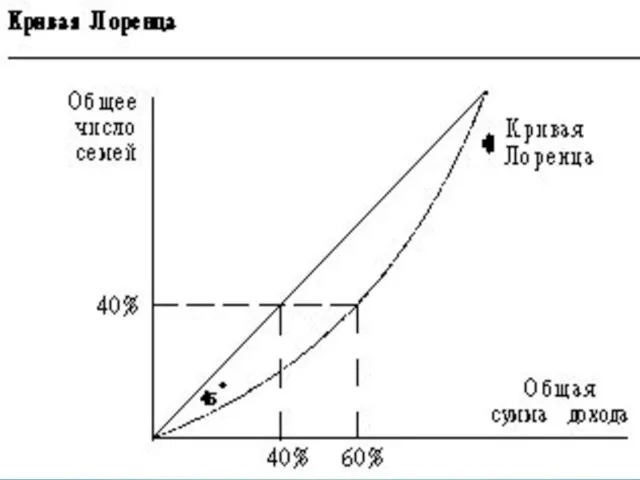
- 51. Для графического изображения неравномерности в распределении доходов строится кривая Лоренца, по которой можно рассчитать коэффициент Джини
- 53. Кривая Лоренца Кривая, которая показывает, какую часть совокупного денежного дохода страны получает каждая доля низкодоходных и
- 55. Графический метод, к которому прибегают экономисты, чтобы проиллюстрировать распределение доходов или сходные процессы. Как можно видеть
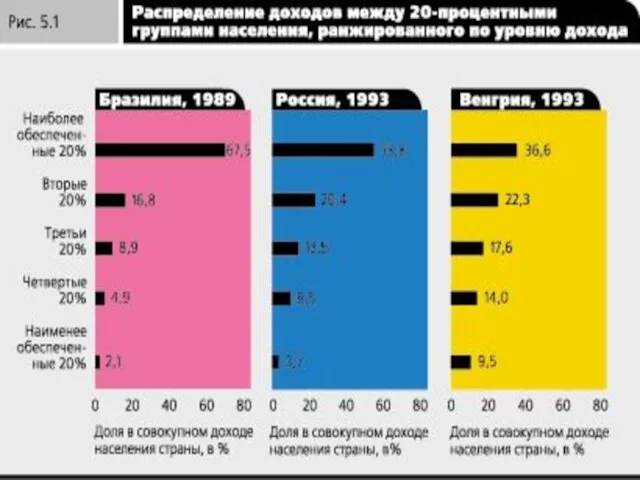
- 56. Различия в распределении доходов в разных странах Для того чтобы представить себе жизнь людей в той
- 58. В России разрыв в доходах между "верхними" и "нижними" 20% группами населения составлял примерно 14:1 в
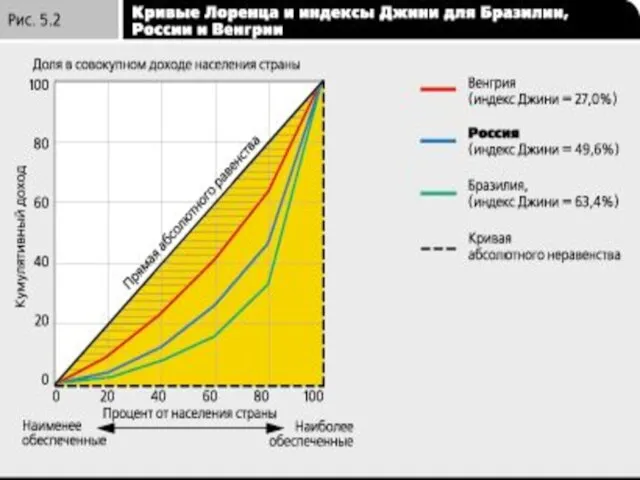
- 59. Чем сильнее изогнута кривая Лоренца страны, тем менее равномерным является распределение доходов в этой стране. Для
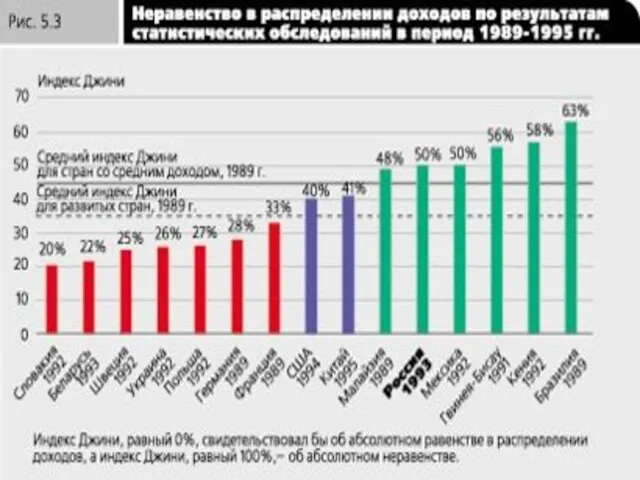
- 61. Для того чтобы сопоставить степень неравенства в распределении доходов сразу во многих странах, еще более удобным
- 63. По официальным подсчетам (версия Росстата), коэффициент Джини для России сейчас приблизительно равен 0,3, что сравнимо с
- 64. При статистическом изучении уровня и границ бедноты устанавливается величина минимально допустимого дохода, для чего используется величина
- 65. К бедному относится население с уровнем располагаемых доходов ниже прожиточного минимума
- 66. Численность такого населения (домашних хозяйств) определяется на основе итогов выборочного обследования домашних хозяйств путем соизмерения располагаемых
- 67. Малоимущее население (домашние хозяйства) с уровнем располагаемых ресурсов в два и более раза ниже величины прожиточного
- 68. Доля численности населения с доходами ниже прожиточного минимума в общей численности населения называется коэффициентом бедности
- 69. Основные показатели бедности определяются формулой, предложенной Джеймсом Фостером James Foster, Джоэлом Гриером Joel Greer и Эриком
- 70. На основе Формулы Фостера-Гриера-Торбеке определяются основные показатели бедности: коэффициент бедности и уровень бедности (а=0) индекс глубины
- 71. Коэффициент бедности Доля бедных домохозяйств в общем количестве домохозяйств Коэффициент бедности характеризует только степень распространения бедности
- 72. Индекс глубины бедности Характеризует среднее отклонение доходов бедных домохозяйств от величины прожиточного минимума и выражается величиной
- 73. Другая встречающаяся редакция общей формулы Nj- численность обследуемых домохозяйств с доходами ниже прожиточного минимума Cminj- величина
- 74. Индекс глубины бедности позволяет оценить насколько ниже относительно черты бедности расположены доходы бедных домохозяйств.
- 75. Индекс остроты бедности
- 76. Индекс остроты бедности характеризует средневзвешенное отклонение доходов бедных домохозяйств от величины прожиточного минимума и выражается величиной
- 77. Дефицит дохода бедных домохозяйств Этот показатель имеет большое значение при разработке программ социальной поддержки малоимущего населения.
- 78. Общая сумма дефицита дохода определяется по следующей формуле: z- черта бедности xi- среднедушевое значение показателя уровня
- 79. Этот показатель означает сумму денежных средств, которой не хватает домохозяйству для достижения границы бедности. Дефицит дохода
- 80. Синтетический индикатор бедности Предложил лауреат Нобелевской премии по экономике за 1998 год Амартия Кумар Сен (родился
- 81. Сен учитывал воздействие таких факторов, как: - распространенность бедности как социального явления - уровень материальной недостаточности
- 82. Р(0)- доля бедного населения I- средний дефицит дохода в процентах к границе бедности (промежуток низкого дохода)
- 83. Другой встречающийся вариант S- индекс Сена L- доля бедного населения N- отношение среднего дефицита дохода к
- 84. Sen-индекс представляет собой взвешенную сумму дефицитов домохозяйств, отнесенных к бедным. Этот показатель варьируется в интервале от
- 85. На основании данных о доходах бедного населения вычисляют показатель дефицита дохода, характеризующий объем денежных средств, недостающий
- 86. Распределение населения России по величине среднедушевых денежных доходов (в процентах)
- 88. Скачать презентацию












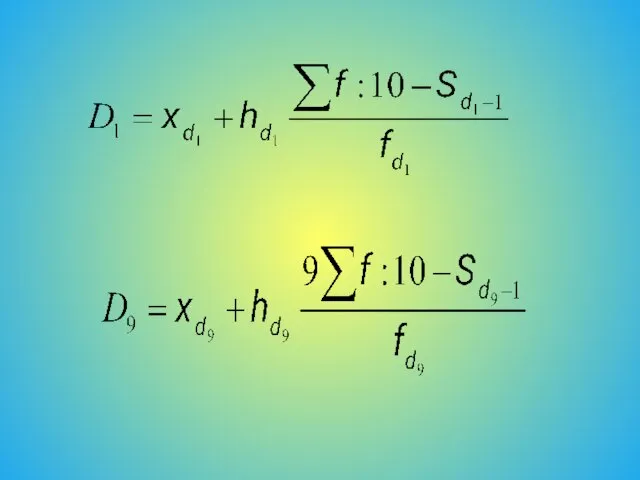

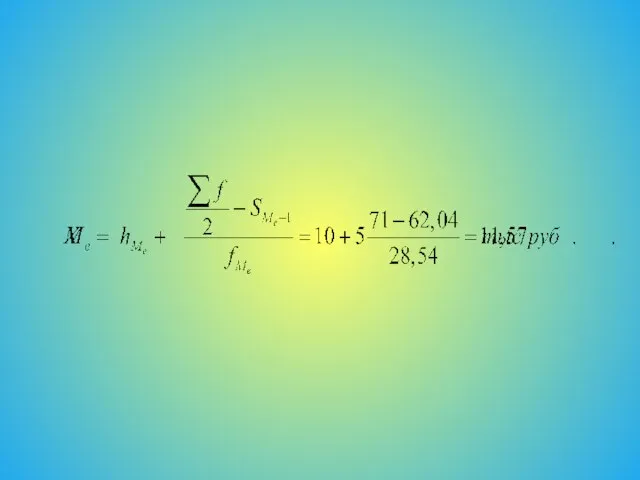

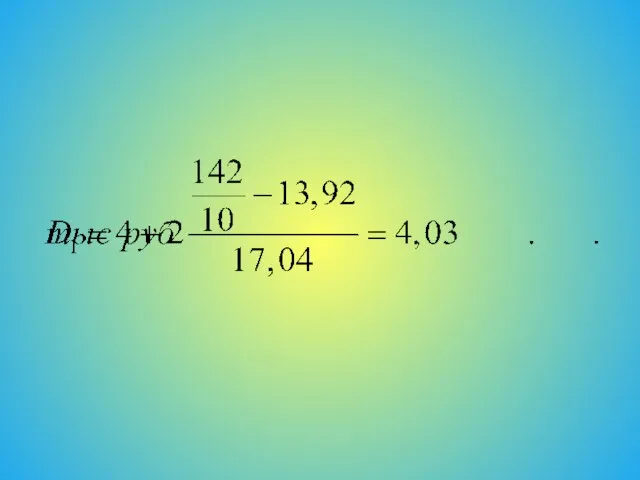



























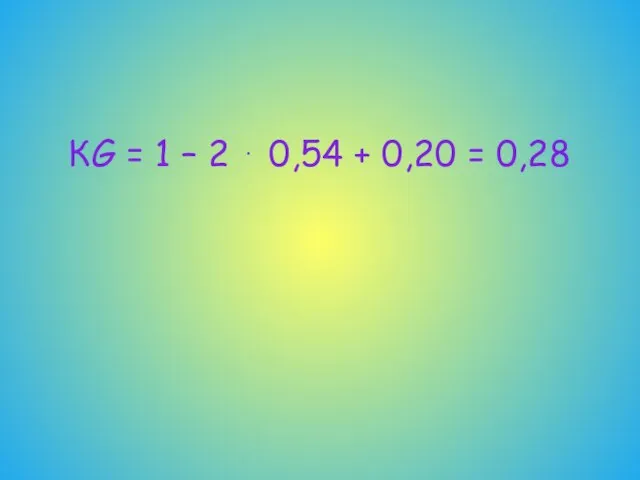
































 Презентация на тему Предложения с вводными конструкциями (8 класс)
Презентация на тему Предложения с вводными конструкциями (8 класс) Салон красоты De’Paris. Издержки
Салон красоты De’Paris. Издержки ВЛАСТЬ и НАРОД в сатире М.Е.Салтыкова-Щедрина «История одного города»
ВЛАСТЬ и НАРОД в сатире М.Е.Салтыкова-Щедрина «История одного города» The system of State bodies of India
The system of State bodies of India Генерация идей и оценка их привлекательности
Генерация идей и оценка их привлекательности ГИПЕРЛИПИДЕМИЯ
ГИПЕРЛИПИДЕМИЯ  Семья и школа
Семья и школа Электронное портфолиоили Персональный сайт учителя
Электронное портфолиоили Персональный сайт учителя ВиртуализацияMicrosoft Application Virtualization 4.6(ранее SoftGrid)Демонстрация.
ВиртуализацияMicrosoft Application Virtualization 4.6(ранее SoftGrid)Демонстрация. Технологическое оборудование
Технологическое оборудование Шаблон проекта
Шаблон проекта Переформулировки поисковых запросов в Яндексе
Переформулировки поисковых запросов в Яндексе Чершкало Светлана Сергеевна
Чершкало Светлана Сергеевна Презентация на тему Малайзия (малайск. Malaysia)
Презентация на тему Малайзия (малайск. Malaysia) 点击添加相关文字内容
点击添加相关文字内容 Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  Задачи по теме
Задачи по теме Новогодние игрушки и поделки (2 часть)
Новогодние игрушки и поделки (2 часть) Методические особенности развития прыгучести у волейболистов
Методические особенности развития прыгучести у волейболистов .
. Пирĕн тăрăхри йывăçсем
Пирĕн тăрăхри йывăçсем Валютный контроль
Валютный контроль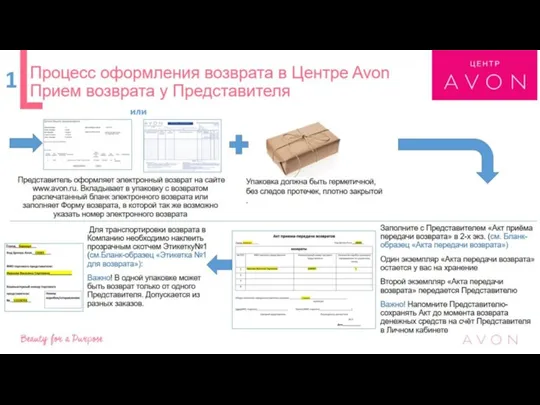 Прием возвратов у представителя в центре Avon
Прием возвратов у представителя в центре Avon Параолимпийцы Оренбургской области
Параолимпийцы Оренбургской области Презентация на тему Оптика Атомная и ядерная физика
Презентация на тему Оптика Атомная и ядерная физика Вироби зі скла. Сходи
Вироби зі скла. Сходи Алан Милн
Алан Милн Я - иллюстратор детских книг
Я - иллюстратор детских книг