Слайд 2Определение.
Функцию вида
называют показательной функцией

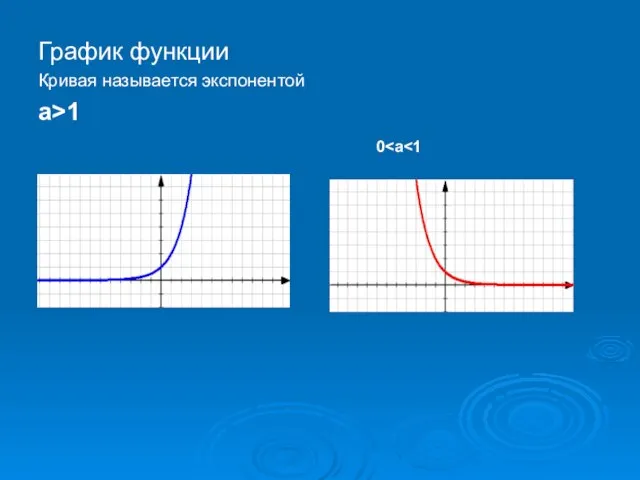
Слайд 4График функции
Кривая называется экспонентой
а>1
0<а<1
Слайд 5Геометрическая особенность графика функции
Ось Ох является горизонтальной асимптотой графика функции
при х→

-∞, если а >1
при х→ +∞, если 0<а<1
Слайд 6Показательными уравнениями
называют уравнения вида
а>0,а≠1,
и уравнения, сводящиеся к этому виду

Слайд 7Основные методы решения показательных уравнений
Функционально-графический
Основан на использовании графический иллюстраций или каких-либо свойств

функции.
Метод уравнивания показателей
Основан на применении теоремы:
Уравнение равносильно уравнению f(x)=g(x),
где а>0,а≠1.
Метод введения новой переменной
Слайд 8Показательные неравенства
Показательными неравенствами называют неравенства вида
а>0,а≠1, и неравенства, сводящиеся к этому виду.
Теорема:

Показательное неравенство
равносильно неравенству f(x)>g(x), если а >1 ;
Показательное неравенство
равносильно неравенству f(x)






 Госзакупки. С чего начать
Госзакупки. С чего начать Социальные деньги и платежи в социальных сетях.Способы монетизации игрового трафика и премиум сервисов.
Социальные деньги и платежи в социальных сетях.Способы монетизации игрового трафика и премиум сервисов. Всього одна чарка
Всього одна чарка ИЗУЧАЕМ EXCEL
ИЗУЧАЕМ EXCEL Институт кураторов — копия
Институт кураторов — копия Богатыри - герои былин
Богатыри - герои былин Острые респираторные заболевания и их профилактика
Острые респираторные заболевания и их профилактика Работа Эйвазова Фарида Школа-лицей 264,8d. Любое вещество может находиться в трёх агрегатных состояниях, таких как: Жидкое Твёрдое Га
Работа Эйвазова Фарида Школа-лицей 264,8d. Любое вещество может находиться в трёх агрегатных состояниях, таких как: Жидкое Твёрдое Га Геометрия в моде
Геометрия в моде Презентация на тему Аллея героев Первой мировой войны
Презентация на тему Аллея героев Первой мировой войны Публичный отчёт по основным направлениям развития 17.02.2011 Муниципальное автономное образовательное учреждение средняя общеобраз
Публичный отчёт по основным направлениям развития 17.02.2011 Муниципальное автономное образовательное учреждение средняя общеобраз CHOOSING A PROFESSION
CHOOSING A PROFESSION внутреннее строение насекомых
внутреннее строение насекомых 984967 (3)
984967 (3) Условие не превышения границы области допустимых состояний конструкции
Условие не превышения границы области допустимых состояний конструкции Положение об общественном совете муниципального образования
Положение об общественном совете муниципального образования Традиции модернизма в искусстве 2-й пол. ХХ века
Традиции модернизма в искусстве 2-й пол. ХХ века Лакомства для домашних питомцев из рога и субпродуктов ТМ Живкус
Лакомства для домашних питомцев из рога и субпродуктов ТМ Живкус Полные квадратные уравнения
Полные квадратные уравнения Сегментация изображений
Сегментация изображений Конституция Республики Молдова
Конституция Республики Молдова Методическая работа школы
Методическая работа школы Набор в секции. Отделение сложно-координационных видов
Набор в секции. Отделение сложно-координационных видов Виктор Федорович Боков
Виктор Федорович Боков Chapter-8. Learning goals
Chapter-8. Learning goals Методи цитологічних досліджень
Методи цитологічних досліджень Реальная государственная поддержка сельского хозяйства! Миссия Корпорации – участие в реализации государственной политики агра
Реальная государственная поддержка сельского хозяйства! Миссия Корпорации – участие в реализации государственной политики агра Использование XSLT для разработки сайтов (на ASP.NET) Андрей Майоров, BYTE-force
Использование XSLT для разработки сайтов (на ASP.NET) Андрей Майоров, BYTE-force