Содержание
- 2. Графические изображения Для наглядного представления тенденции изменения наблюдаемых значений применяют графическое изображение статистического материала. Наиболее распространенными
- 3. Гистограмма плотности распределения Что это такое? Когда это применяется? Как это применяется?
- 4. Что это такое? Гистограмма плотности распределения — это столбиковая диаграмма, которая показывает, как данные распределяются по
- 5. Когда это применяется? Гистограмму плотности распределения используют, чтобы наглядно показать, в каком интервале располагаются наиболее часто
- 6. Гистограмма позволяет определить наилучшие результаты процесса, а графическое изображение динамики процесса дает возможность наметить приоритетные задачи
- 7. Как это применяется? (нч.) Последовательность шагов при построении гистограммы такова: Проведите необходимые измерения и подсчитайте, сколько
- 8. Как это применяется? (пр.) Разбейте эти значения на группы (или интервалы) и подсчитайте число значений в
- 9. Как это применяется? (пр.) Табл.* Рекомендации для определения количества интервалов гистограммы
- 10. Определите число значений в каждом интервале (ширину интервала) следующим образом: делением разброса на минимальное число интервалов;
- 11. Составьте таблицу плотности распределения всех значений. Постройте на основе таблицы плотности распределения гистограмму плотности распределения. Отметьте
- 12. Пример 1 (нч.) ЦЕЛЬ РАБОТЫ: Управляющий людскими ресурсами одной организации решил проанализировать, сколько времени уходит на
- 13. Пример (пр.) Время, затраченное на подбор новых служащих (в рабочих днях): 32 27 27 36 31
- 14. Пример (пр.) 2. Далее он выполнил следующие расчеты: число значений показателя равно 55 (число интервалов —
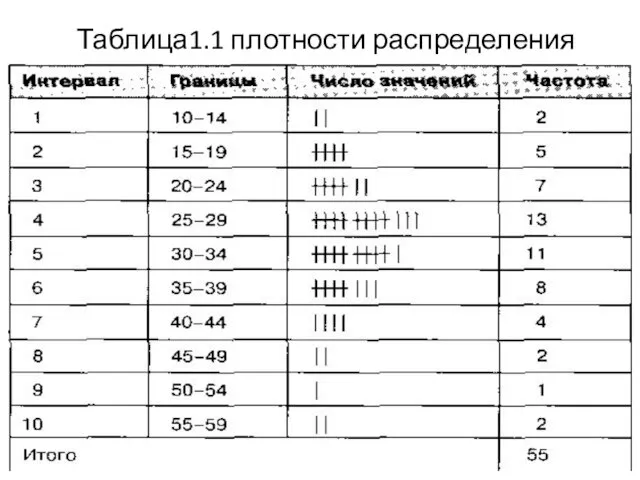
- 15. Пример (пр.) 3. Составляет таблицу плотности распределения (см. табл. 1.1) и строит на ее основе соответствующую
- 16. Таблица1.1 плотности распределения
- 17. *)Примечание к табл. 1.1 Контрольный листок для регистрации несоответствий, например, дефектов (см. л.1). Порядок заполнения: каждый
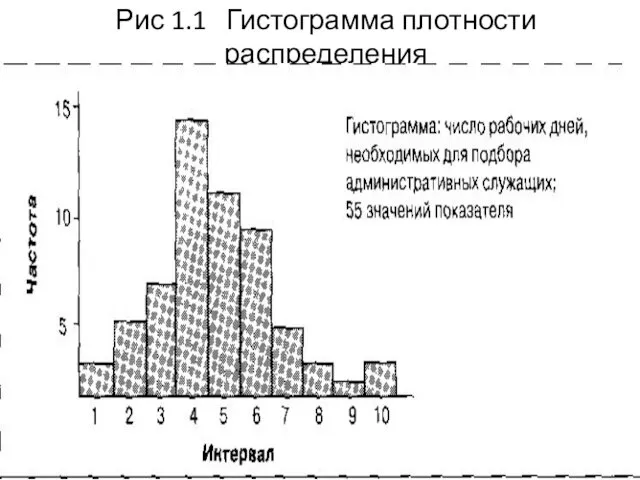
- 18. Рис 1.1 Гистограмма плотности распределения
- 19. Пример 1 (ок.) Гистограмма показывает, что в большинстве случаев процедура подбора служащих занимала от 25 до
- 20. Инструменты контроля качества Гистограмма — удобный инструмент, позволяющий зрительно оценить закон распределения статистических данных. Но не
- 21. Три способа графического представления данных (нч) Отдавая должное гистограмме, рассмотрим все основные способы графического представления данных,
- 22. Полигоны применяют: - как правило, для отображения дискретных изменений значений случайной величины; - но они могут
- 23. Использование полигонов при непрерывных (интервальных) изменениях: - ординаты, пропорциональные частотам интервалов, восстанавливаются перпендикулярно оси абсцисс в
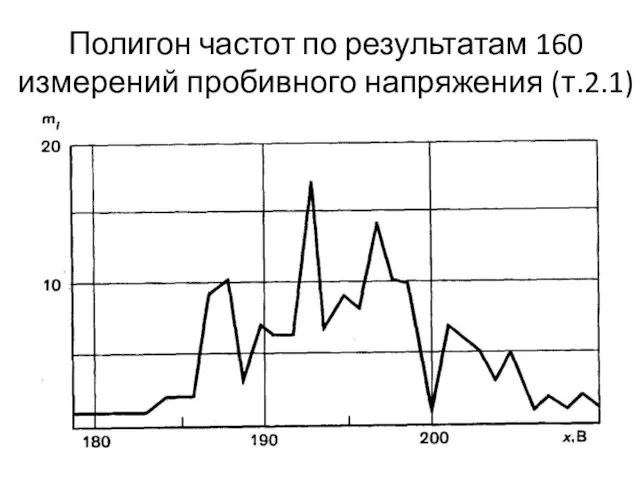
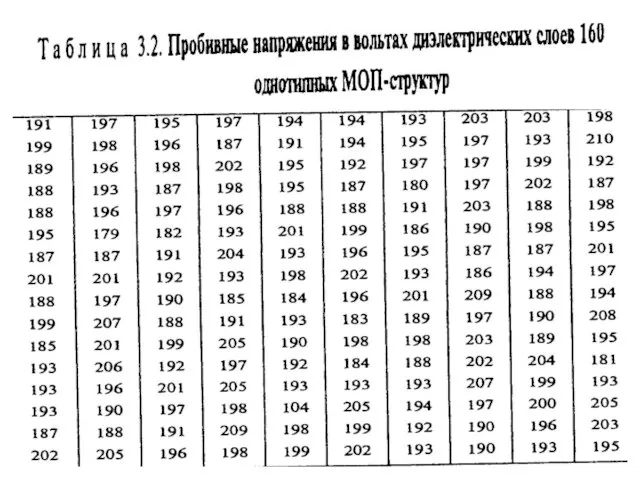
- 24. Пример 2 изображение значений пробивного напряжения в виде полигона, взятых из табл. 2.1, приведен на рис.
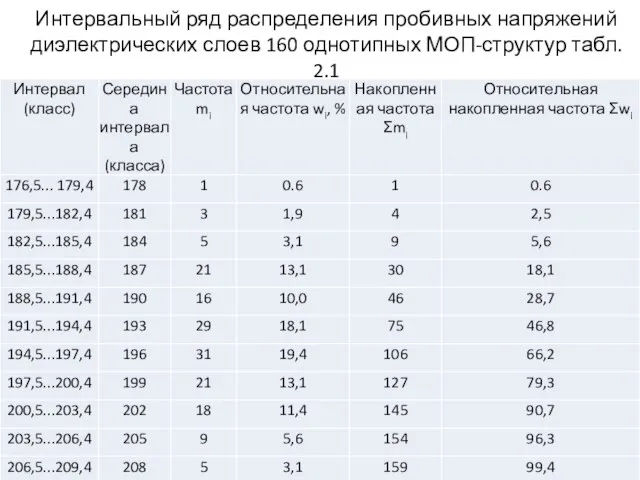
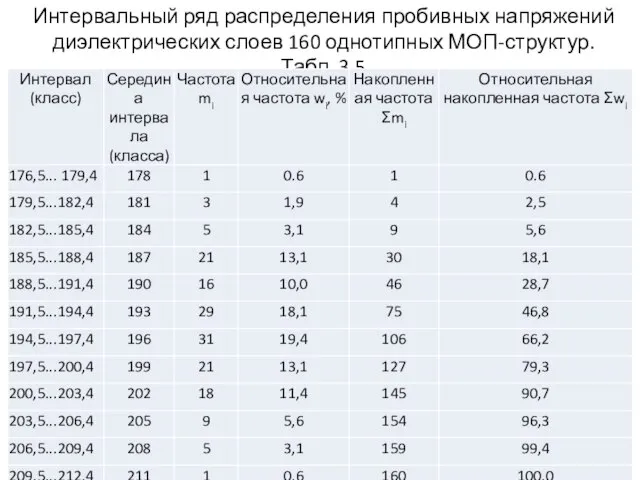
- 25. Интервальный ряд распределения пробивных напряжений диэлектрических слоев 160 однотипных МОП-структур табл. 2.1
- 26. Полигон частот по результатам 160 измерений пробивного напряжения (т.2.1)
- 27. Гистограмма распределения обычно строится для интервального изменения значения параметра. Для этого на интервалах, отложенных на оси
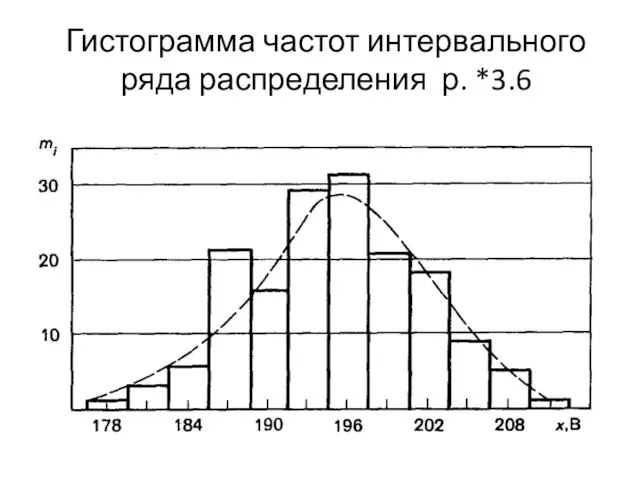
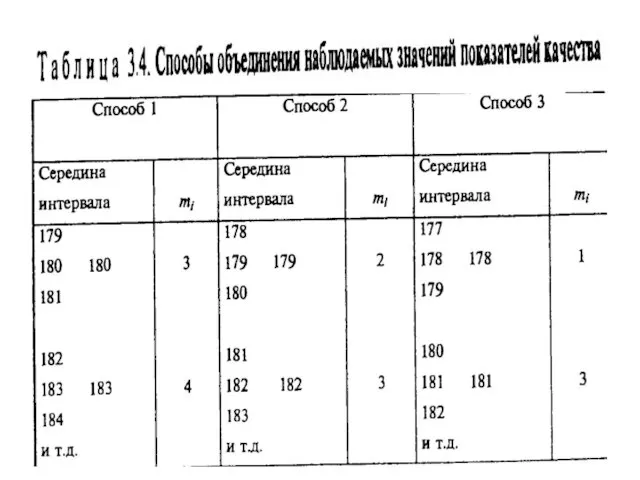
- 28. Гистограмма интервального ряда, значения которого взяты из табл. 3.4 (способ 3), изображена на рис. *3.6, где
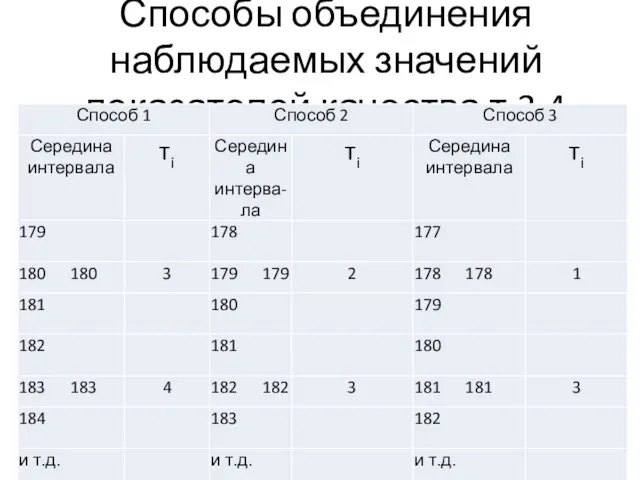
- 29. Способы объединения наблюдаемых значений показателей качества т.3.4
- 30. Гистограмма частот интервального ряда распределения р. *3.6
- 31. Гистограмма частот интервального ряда распределения Аналогичную форму гистограммы можно получить, если по оси ординат на рис.
- 32. Интервальный ряд распределения пробивных напряжений диэлектрических слоев 160 однотипных МОП-структур. Табл. 3.5
- 33. Сумма площадей = 1 Если на рис. 3.6 ширину класса (2,9) принять за единицу шкалы по
- 34. Кривая плотности вероятностей Если на рис. 3.6 кроме гистограммы нанести и полигон, то по мере роста
- 35. Площадь полигона = 1 Площадь, ограниченная полигоном и осью абсцисс, в том случае, если по оси
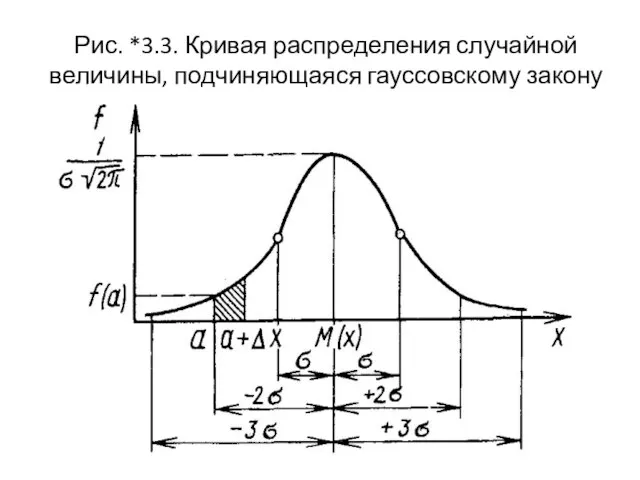
- 36. Рис. *3.3. Кривая распределения случайной величины, подчиняющаяся гауссовскому закону
- 37. Технология обработки (нч.) Для выяснения того, соответствует ли данное распределение результатов измерения нормальному распределению, иногда используют
- 38. Представление данных на вероятностной бумаге осуществляется следующим способом: 1) На основе полученных в результате измерения параметров
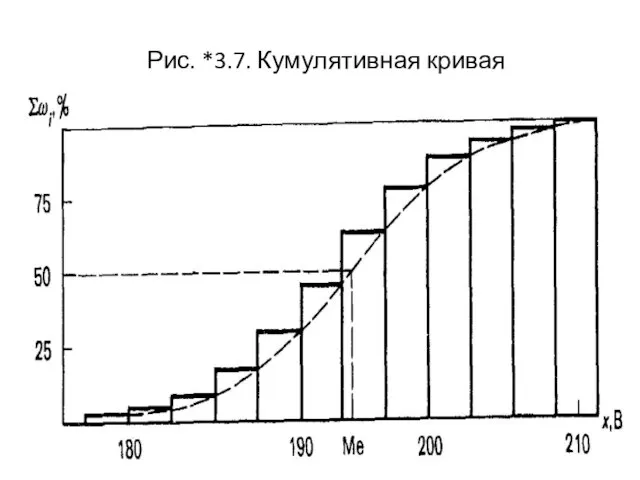
- 39. Кумулятивная кривая 2) Накопленная частота (частость) каждого значения параметра качества получается суммированием всех частот (частостей), предшествующих
- 40. Накопленные частоты (частости) интервального ряда относятся к верхним границам интервалов, а не к серединам каждого из
- 41. Накопленный полигон Зависимость на рис. *3.7 представляет собой полигон, построенный на основе таблиц накопленных частот (см.
- 42. Рис. *3.7. Кумулятивная кривая
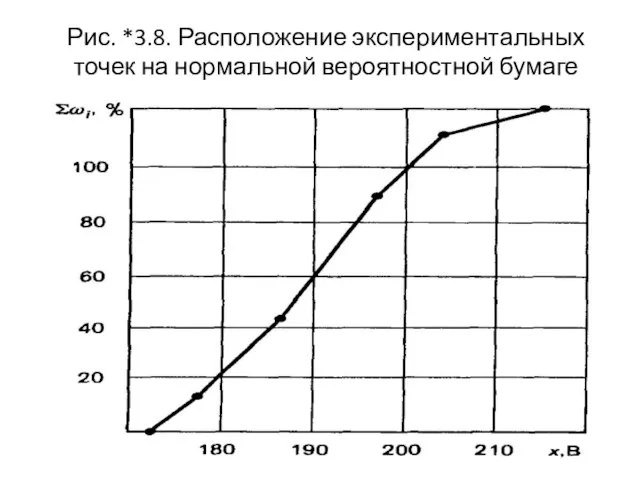
- 43. Рис. *3.8. Расположение экспериментальных точек на нормальной вероятностной бумаге
- 44. Кумулятивная кривая имеет более плавный характер изменения, чем гистограмма или полигон частот, ибо накопление приводит к
- 45. В результате имеют на ней шесть точек: - три точки, соответствующие большему значению параметра качества относительно
- 46. В примере точки не легли точно на прямую, но оказались довольно близко к ней. Можно сделать
- 47. Преимущества гистограммы Из рассмотренных графических изображений становится понятным преимущество гистограммы при визуальной оценке закона распределения случайной
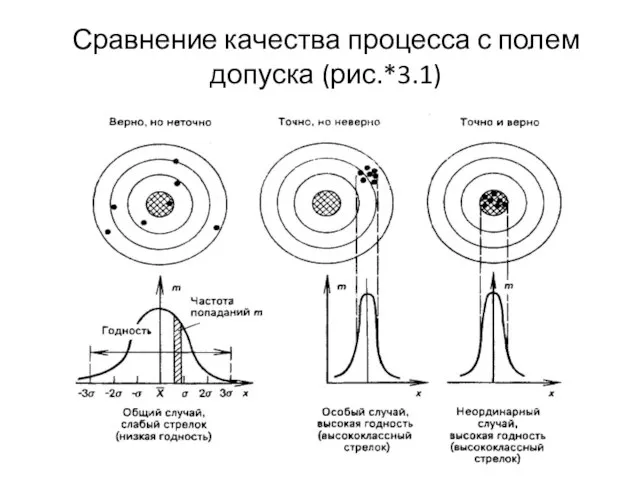
- 48. Связь с требованиями потребителя Чтобы оценить адекватность процесса требованиям потребителя, следует сравнить качество процесса с полем
- 49. Сравнение качества процесса с полем допуска (рис.*3.1)
- 50. Если имеется допуск, то на гистограмму наносят верхнюю (SU) и нижнюю (SL) его границы в виде
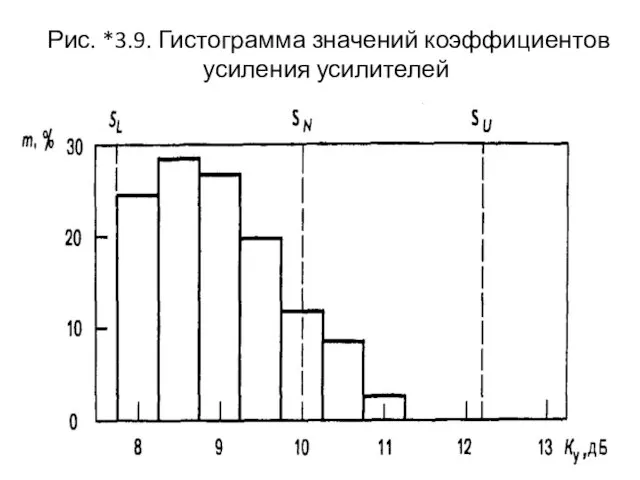
- 51. Пример (нч) На рис. *3.9 приведена гистограмма значений коэффициентов усиления 120 проверенных усилителей. В технических условиях
- 52. Рис. *3.9. Гистограмма значений коэффициентов усиления усилителей
- 53. Пример (пр.) Номинальное значение представляет собой математическое ожидание, т.е. среднее значение коэффициента усиления для данного типа
- 54. Допустимые пределы SL и SU В ТУ установлены допустимые пределы изменения коэффициента усиления: - нижняя граница
- 55. Отсутствие проблем? Если расположить все 120 значений коэффициентов усиления в ранжированный ряд, то: - можно было
- 56. Гистограмма информативнее В отличие от сделанного выше заключения гистограмма сразу показывает, что распределение коэффициентов усиления хотя
- 57. Гистограмма информативнее (пр) По изображенному распределению на гистограмме можно выяснить, в удовлетворительном ли состоянии находятся партии
- 58. Для выяснения проблемных моментов, исходя из установленных допусков рассматривают следующие вопросы: - какова широта распределения по
- 59. По форме распределения, которая легко «вырисовывается – читается», рассмотрим, какие меры можно принимать в различных случаях.
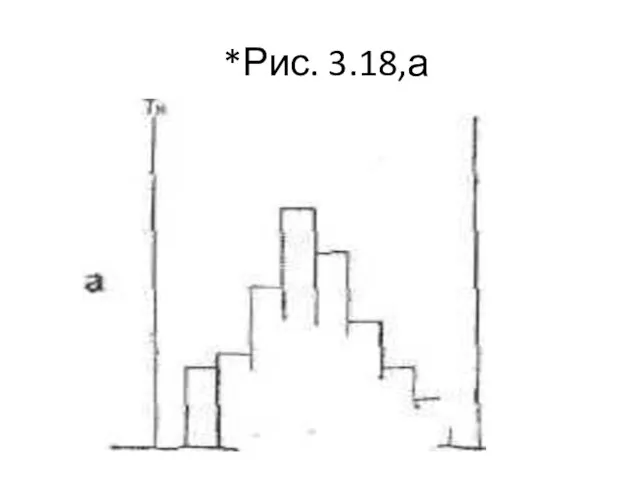
- 60. *Рис. 3.18,а
- 61. На рис. 3.18,а видно, что форма распределения удовлетворительна, ибо ее левая и правая стороны симметричны. Если
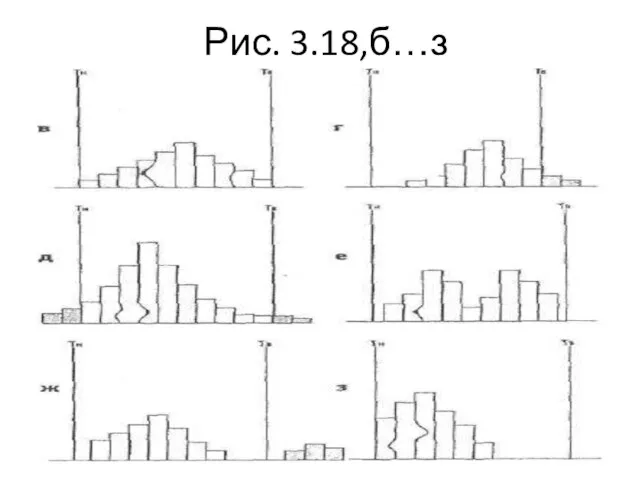
- 62. Рис. 3.18,б…з
- 63. На рис. *3.18,б форма распределения отклонена вправо, поэтому центр распределения тоже смещен. Имеется опасение, что среди
- 64. На рис. *3.18,в центр распределения расположен правильно, однако, поскольку широта распределения совпадает с широтой поля допуска,
- 65. На рис. *3.18,г центр распределения смещен, что говорит о присутствии дефектных изделий. Так как широта распределения
- 66. На рис. *3.18,д центр распределения совпадает с центром поля допуска, но широта распределения превышает широту поля
- 67. На рис. *3.18,е распределение имеет два пика, хотя образцы взяты из одной партии. Это явление объясняется
- 68. На рис. *3.18,ж (нч) главные части распределения (широта и центр) в норме, однако незначительная часть изделий
- 69. На рис. *3.18,ж (ок) Изделия, выделенные на «островке», возможно, представляют собой часть дефектных изделий, которые могли
- 70. Рассмотрим случай, когда гистограмма имеет симметричный вид ("колокол") ─ ─ можно предполагать гауссовский закон распределения случайной
- 71. Если предполагать, что гистограмма следует нормальному (гауссовому) закону распределения, то возможно исследование воспроизводимости процесса, т.е. определяется
- 72. *Стандартное отклонение Стандартное отклонение — классический индикатор изменчивости из описательной статистики. Спасибо Карлам (Гауссу и Пирсону)
- 73. *Стандартное отклонение, среднеквадратичное отклонение, СКО, выборочное стандартное отклонение (англ. standard deviation, STD, STDev) — очень распространенный
- 74. *Вычисление СКО Самостоятельное вычисление СКО вряд ли понадобиться, т.к. основные программы обработки данных имеют встроенную функцию
- 75. Стандартное отклонение можно определить как корень из суммы квадратов разниц между элементами выборки и средним, деленной
- 76. Знание стандартного отклонения во времени важно при оценке процесса с помощью выборочных данных, когда требуется выяснить:
- 77. Нормальное распределение Если процесс имеет нормальное распределение, то легко определить возможность выхода распределения генеральной совокупности при
- 78. Необходимо учитывать следующую особенность: Из рис. *3.10, *3.11 (данные табл. *3.6), видно, что если брать в
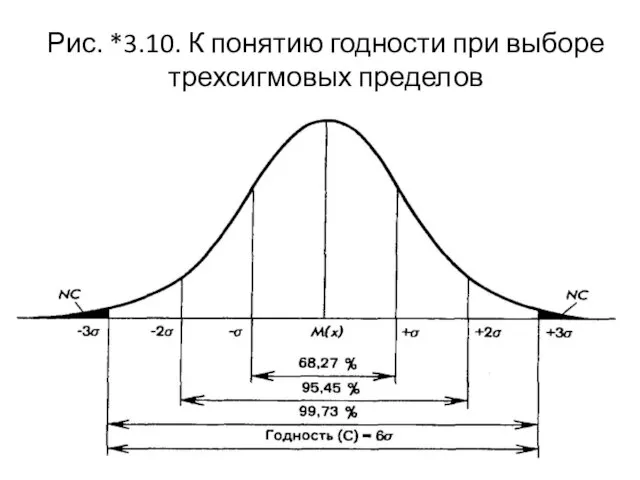
- 79. Рис. *3.10. К понятию годности при выборе трехсигмовых пределов
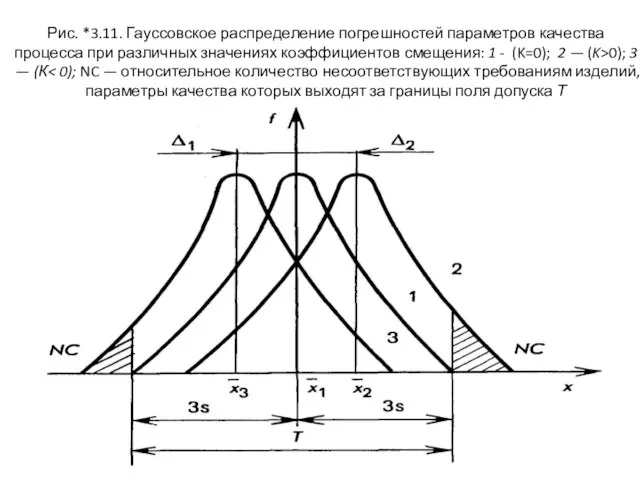
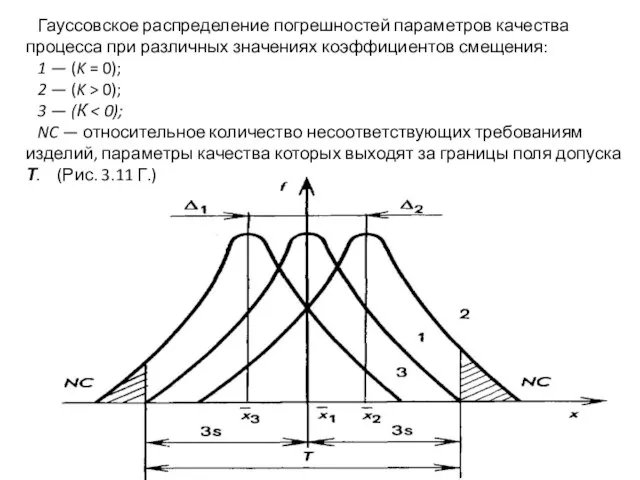
- 80. Рис. *3.11. Гауссовское распределение погрешностей параметров качества процесса при различных значениях коэффициентов смещения: 1 - (K=0);
- 81. В итоге, при рассматриваемом подходе часть годных данных (
- 82. Годные Предполагаемые годные (соответствующие трехсигмовым пределам) данные будем обозначать через С (conformity) и их количество будет
- 83. Коэффициент годности Для количественной оценки того, сколько из предполагаемых годных данных (conformity) вошло в поле допуска,
- 84. Коэффициент годности является частным случаем коэффициента точности, который применяется при анализе воспроизводимости процесса по критериям точности
- 85. Точность технологического процесса оценивают исходя из следующих критериев: КТ КТ = 0,76-0,98 — требует внимательного наблюдения;
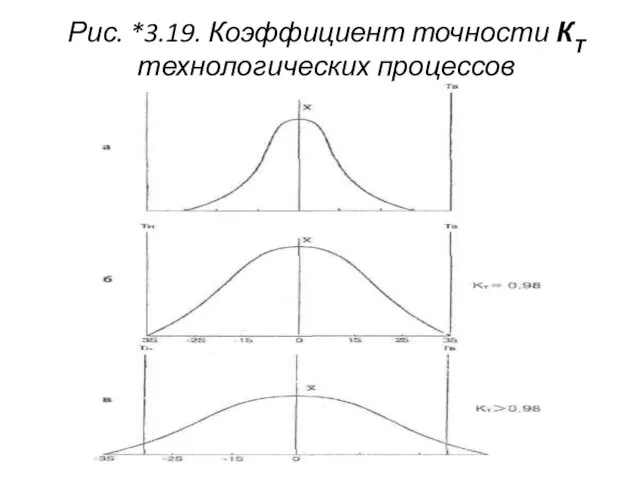
- 86. На рис. *3.19 а, б, в изображён коэффициент точности технологических процессов для случаев: а — точность
- 87. Рис. *3.19. Коэффициент точности КТ технологических процессов
- 88. В зарубежной литературе отношение Сp принято называть отношением или индексом годности. Исследование воспроизводимости процесса с помощью
- 89. Коэффициент смещения Для оценки вклада систематических изменений в протекание процесса применяют индекс годности, который называют коэффициентом
- 90. Коэффициент смещения определяют по формуле: (3) где Δ — абсолютное смещение среднего значения контролируемого параметра от
- 91. Гауссовское распределение погрешностей параметров качества процесса при различных значениях коэффициентов смещения: 1 — (K = 0);
- 92. На практике часто для оценки смещения среднего значения применяют индекс годности Сpk , когда в знаменателе
- 93. Когда Х не смещено от центра поля допуска, т.е. (SU-… ) = (…-SL), то значение Сpk
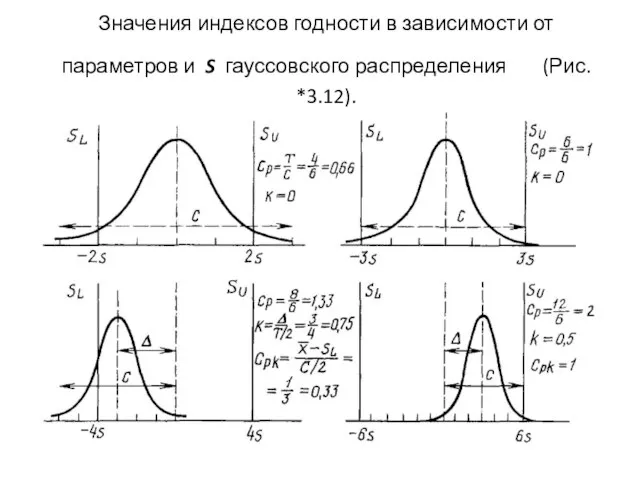
- 94. Когда достаточно Сp ? Для оперативной количественной оценки (рис. *3.12) удовлетворительности хода процесса достаточно применения индекса
- 95. Значения индексов годности в зависимости от параметров и S гауссовского распределения (Рис. *3.12).
- 96. (Нч) Пример составления гистограмм Проблема производителя На предприятии, производящем детали из листовых заготовок, после термообработки были
- 97. Из ведущих специалистов предприятия создана группа экспертов, которая пришла к выводу: главными особыми причинами возникновения дефекта
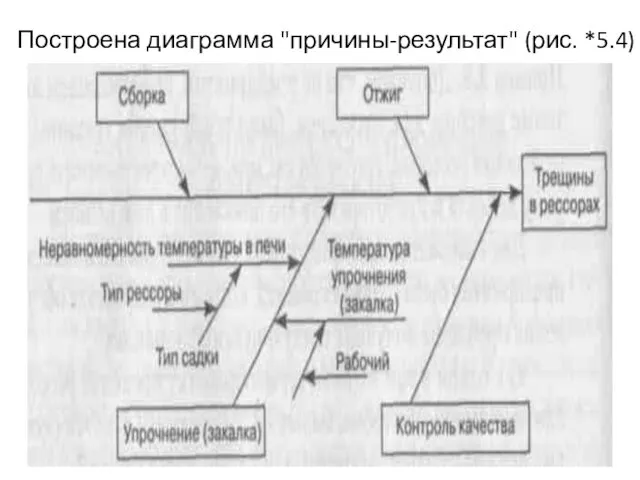
- 98. Построена диаграмма "причины-результат" (рис. *5.4)
- 99. Мероприятия (нч) Разработаны мероприятия по выявлению причин дефекта, в которых намечалось проведение ежедневно (в течение 16
- 100. Мероприятия (пр) Одновременно предложено измерить твердость всех изготовленных деталей, в которых в течение этих 16 дней
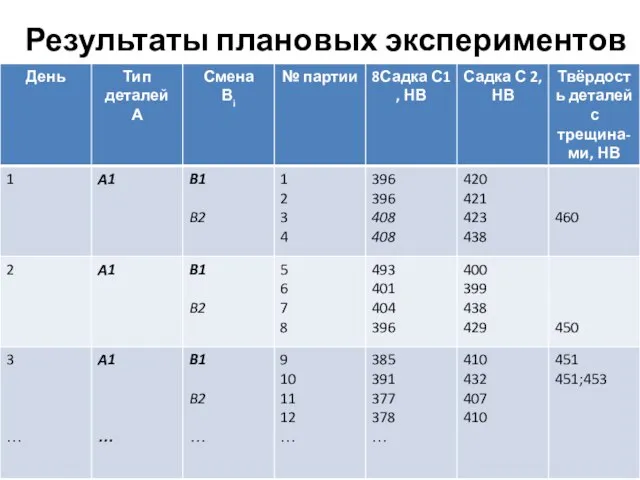
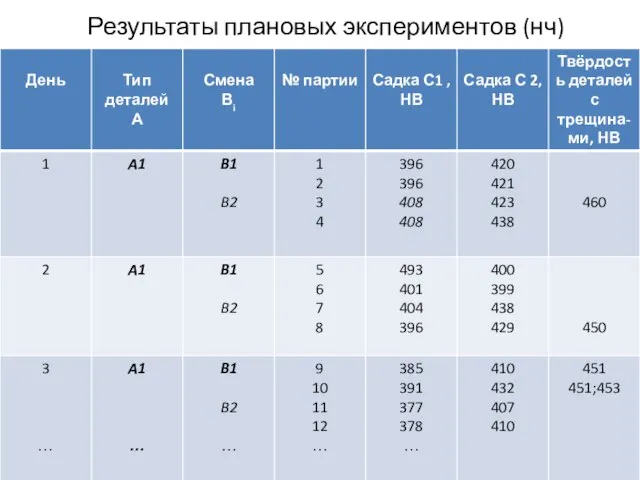
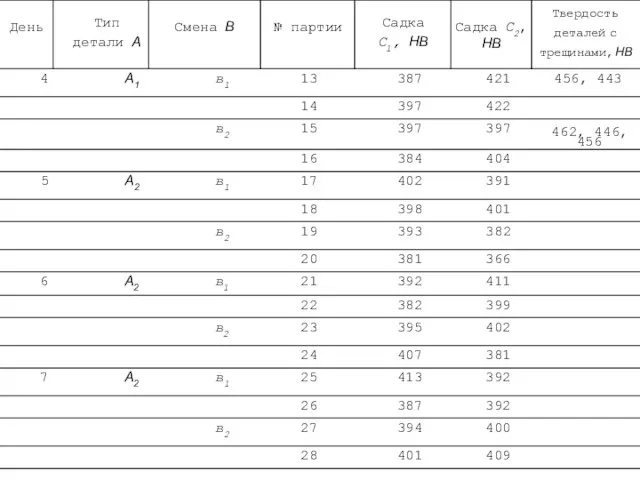
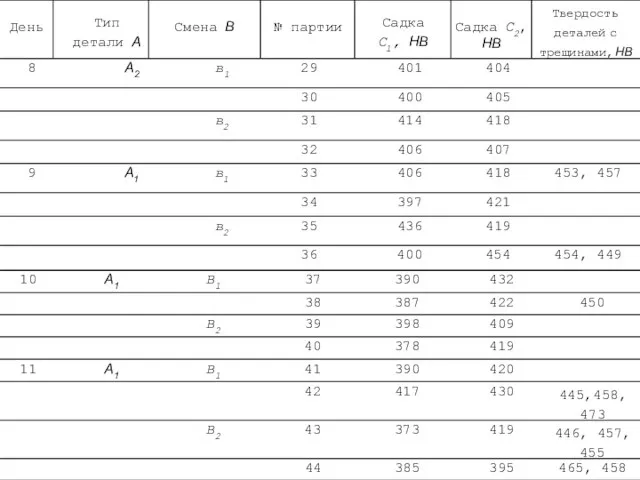
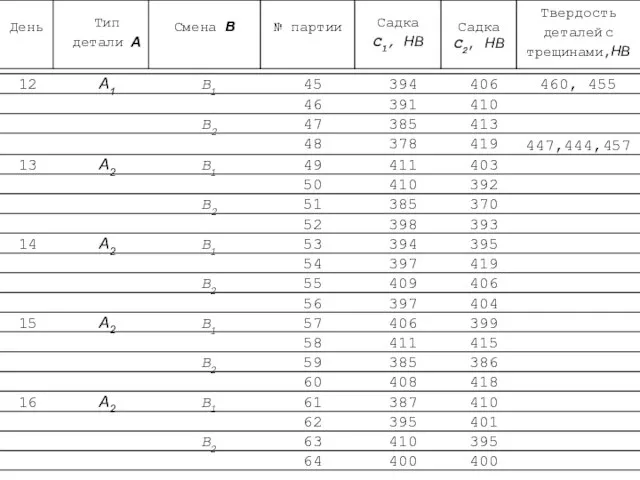
- 101. Результаты плановых экспериментов
- 102. Результаты плановых экспериментов (нч)
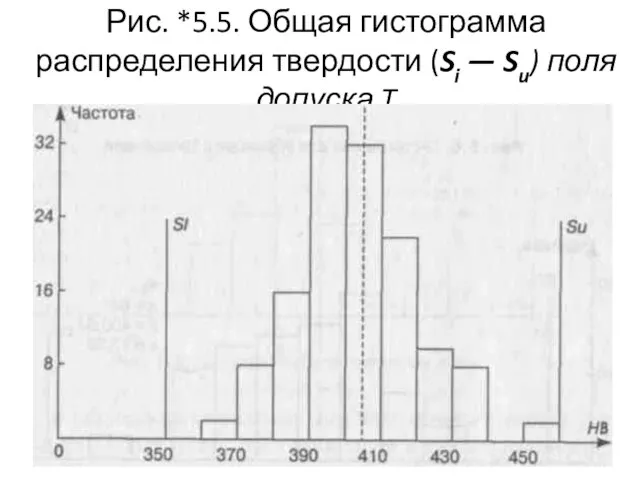
- 106. По результатам всех измерений твердости была построена общая гистограмма (рис. *5.5). Гистограмма демонстрирует приблизительно нормальное распределение,
- 107. Рис. *5.5. Общая гистограмма распределения твердости (Si — Su) поля допуска T
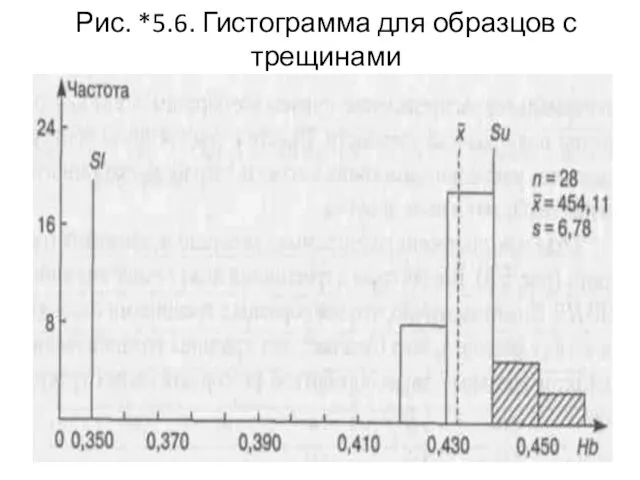
- 108. Рис. *5.6. Гистограмма для образцов с трещинами
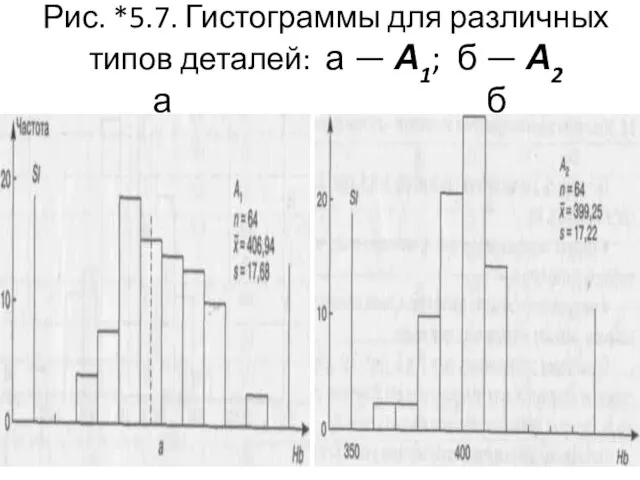
- 109. Детали Гистограммы для различных типов деталей А1 и А2 (рис. *5.7) свидетельствуют, что: ■ средняя твердость
- 110. Рис. *5.7. Гистограммы для различных типов деталей: а — А1; б — А2 а б
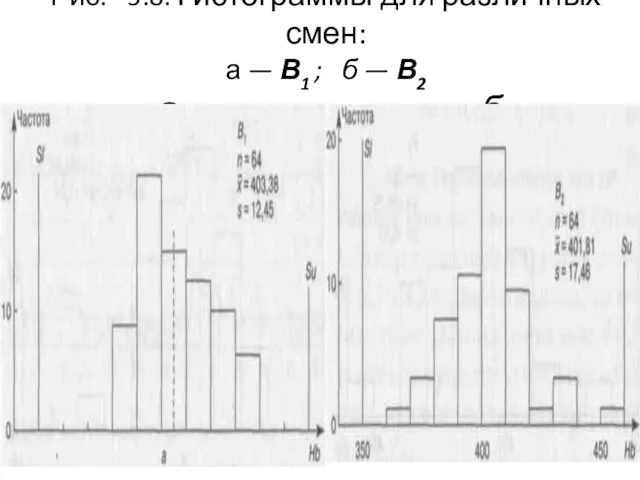
- 111. Смены Гистограммы для различных смен В1 и В2 (рис. *5.8) существенно не отличаются, хотя поле рассеяния
- 112. Рис. *5.8. Гистограммы для различных смен: а — В1 ; б — В2 а б
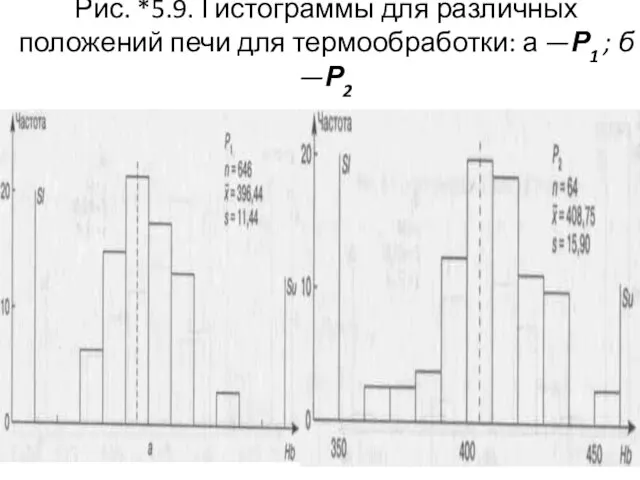
- 113. Садки Гистограммы для различных садок образцов в печи С1 и С2 (рис. *5.9) показывают, что: ■
- 114. Рис. *5.9. Гистограммы для различных положений печи для термообработки: а —Р1 ; б —Р2 а б
- 115. Анализ гистограмм факторов А и В для различных комбинаций факторов А и В показал: - что
- 116. Анализ гистограмм факторов А, В и С для различных комбинаций факторов А, В и С показал:
- 117. Окончательные выводы для рассмотренного примера, можно сделать ограничившись анализом гистограмм, приведённых выше. Однако представляет интерес и
- 118. Приложение
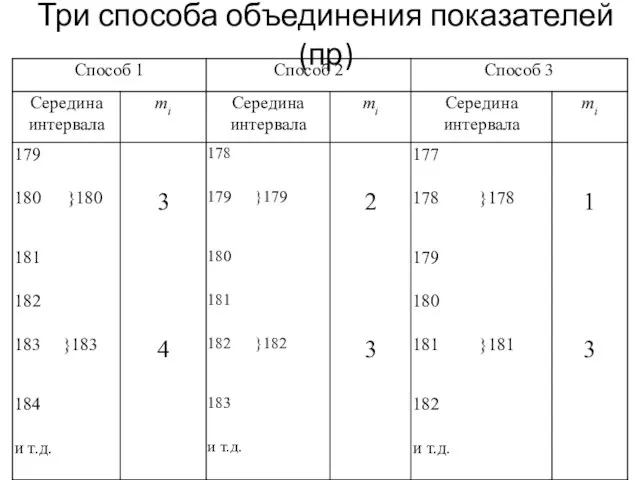
- 122. Три способа объединения показателей (пр)
- 124. Скачать презентацию
























































































 Презентация на тему Прощай, Азбука! 1 класс
Презентация на тему Прощай, Азбука! 1 класс Басни И.А.Крылова
Басни И.А.Крылова Презентация на тему Русская философия
Презентация на тему Русская философия  Проект - робокоптер. Охраняем природу от браконьеров
Проект - робокоптер. Охраняем природу от браконьеров Moschino и художник Бен Фрост. Капсульная коллекция
Moschino и художник Бен Фрост. Капсульная коллекция Прикладные аспекты использования идентификаторов семейства eToken
Прикладные аспекты использования идентификаторов семейства eToken Моё увлечение кошки и черепахи!
Моё увлечение кошки и черепахи! Конструкция сооружений: часть и целое
Конструкция сооружений: часть и целое Рыцарский замок
Рыцарский замок Фотографии для акции Край родной навек любимый. Республика Тыва
Фотографии для акции Край родной навек любимый. Республика Тыва Муниципальная долгосрочная целевая программа «Профилактика правонарушений в городе Волгодонске на 2011-2013гг.»Отчет за I полугод
Муниципальная долгосрочная целевая программа «Профилактика правонарушений в городе Волгодонске на 2011-2013гг.»Отчет за I полугод Почвенные ресурсы России
Почвенные ресурсы России NGPC.RUг. Москва25-26 ноября 2011 г.
NGPC.RUг. Москва25-26 ноября 2011 г. 11а Благословений потоки
11а Благословений потоки Презентация на тему Пропедевтические и интегрированные приёмы воспитания нравственности младших школьников на уроках ОПК
Презентация на тему Пропедевтические и интегрированные приёмы воспитания нравственности младших школьников на уроках ОПК Введение в инженерную деятельность. Трек 5
Введение в инженерную деятельность. Трек 5 Операционная деятельность в логистике. ПОЧУ Улан-Удэнский торгово-экономический техникум. Аксёнова Александра
Операционная деятельность в логистике. ПОЧУ Улан-Удэнский торгово-экономический техникум. Аксёнова Александра Diary
Diary Антропонимы на параллели
Антропонимы на параллели Развитие критического мышления на уроках литературы в 5 классе
Развитие критического мышления на уроках литературы в 5 классе Во всем мне хочется дойти до самого конца Б. Пастернак
Во всем мне хочется дойти до самого конца Б. Пастернак Презентация на тему Экологическое воспитание младших школьников
Презентация на тему Экологическое воспитание младших школьников Периодическая система химических элементов Д.И. Менделеева
Периодическая система химических элементов Д.И. Менделеева Реквием памяти поэтов, павших в годы Великой Отечественной войны.
Реквием памяти поэтов, павших в годы Великой Отечественной войны. Боевой путь тихвинских ополченцев в 1812 – 1814 годах.
Боевой путь тихвинских ополченцев в 1812 – 1814 годах. Повышайте посещаемость вашего сайта
Повышайте посещаемость вашего сайта Трудовое право. (Обществознание. 10 класс)
Трудовое право. (Обществознание. 10 класс) Интерактивная игра по книге М. Твена «Приключения Тома Сойера»
Интерактивная игра по книге М. Твена «Приключения Тома Сойера»