Слайд 2Геометрико-топологические модели в современной науке.
Модели-посредник между теоретическими построениями и компьютерными методами расчетов.
Решетки,

сетки, симплициальные и кубические комплексы, многообразия…
Многомерность и комбинаторная сущность квантовых систем ? как это отразится на суперкомпьютерах следующих поколений?
Слайд 3Кубические структуры.
Многие комбинаторные структуры вложимы в кубические комплексы.
Комплексы изучаются в пространствах Rnc
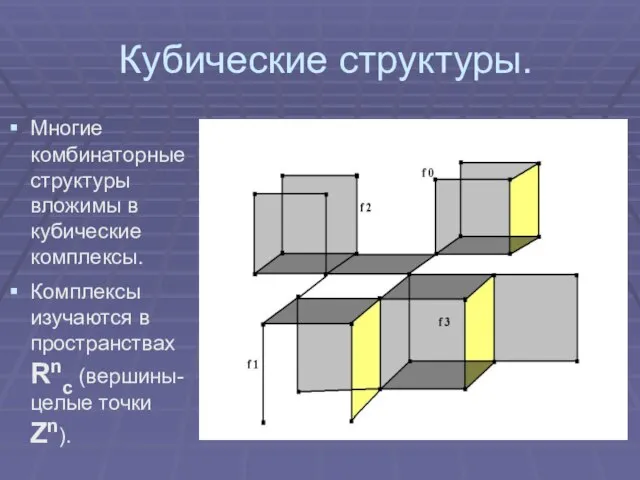
(вершины- целые точки Zn).
Слайд 4Глобальная модель климата (MIT gcm) и корректирующие коды.
Кубическая сфера с конформной решеткой

– база всех климатических расчетов.
Хэммингово расстояние между кодами- вершинами n-куба – базовая мера в теории корректирующих кодов.
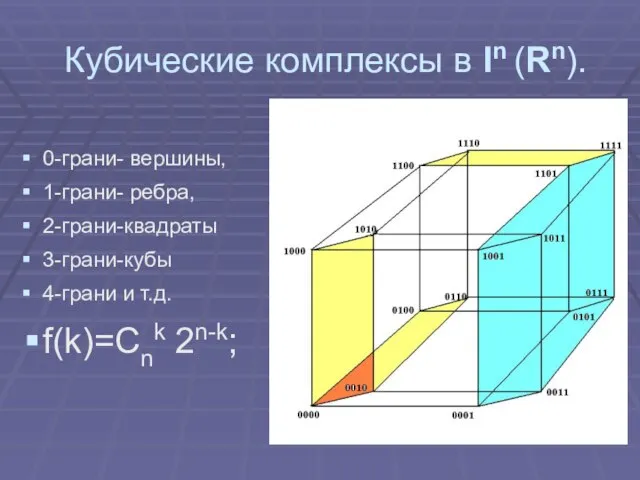
Слайд 5Кубические комплексы в In (Rn).
0-грани- вершины,
1-грани- ребра,
2-грани-квадраты
3-грани-кубы
4-грани и т.д.
f(k)=Cnk 2n-k;
Слайд 6Пирамида Паскаля и k-мерные грани n-куба.
Пирамида Паскаля-рекурсивная процедура в трехмерной решетке.
Сумма чисел
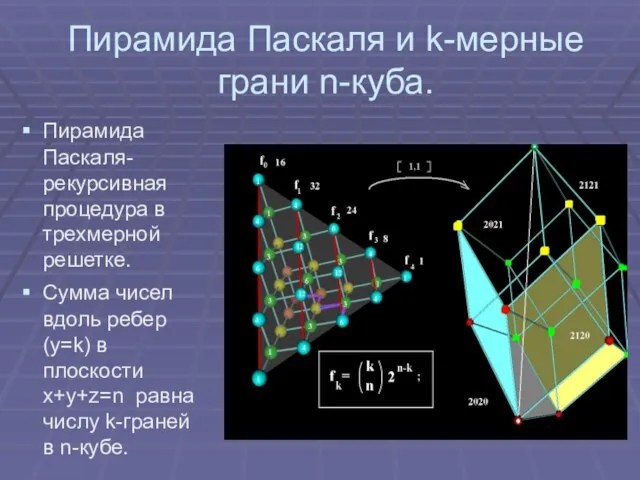
вдоль ребер (y=k) в плоскости х+y+z=n равна числу k-граней в n-кубе.
Слайд 7Биекция: множество всех n-разрядных троичных кодов??множество всех граней n-куба.
E=e1,e2,…ei,…en; ? Rn;
D=d1,d2,…di,…dn;

di?{0,1,2};
E?D; ei?di;
021221?e2xe4xe5 транс. в вершину 001001; трехмерная грань(куб) в шестимерном кубе.
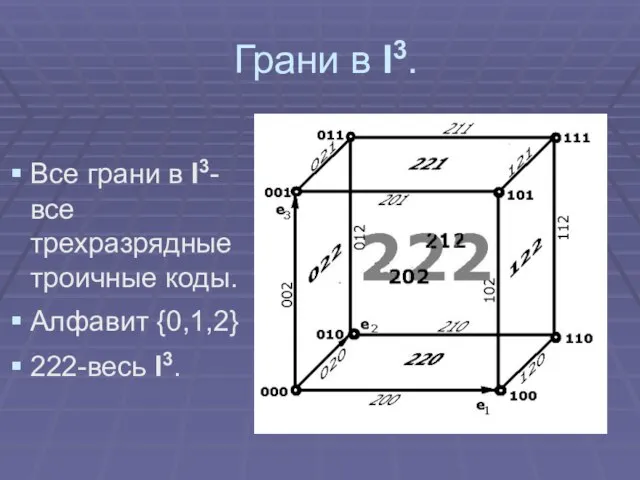
Слайд 8Грани в I3.
Все грани в I3- все трехразрядныетроичные коды.
Алфавит {0,1,2}
222-весь I3.
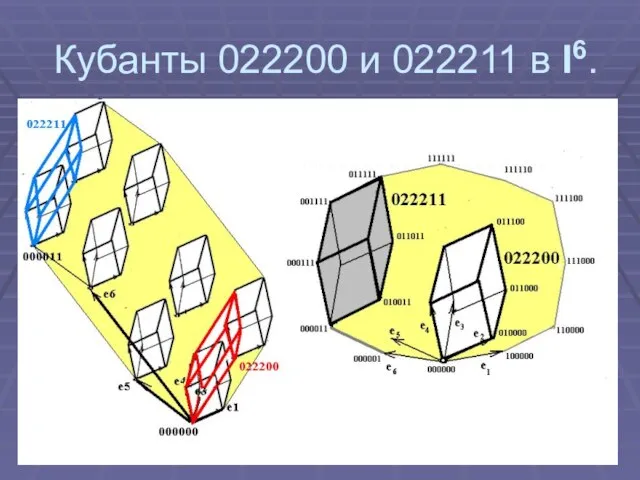
Слайд 9Кубанты
Кубант в n-мерном евклидовом простанстве –троичный n-разрядный код, отражающий размерность грани и

ее положение в n-мерном единичном кубе.
Слайд 11Комплексы из кубантов в I6.
a).Комплекс из 3-х кубантов (3-куб,3-куб,4-куб).
b).Комплекс из 9-и кубантов
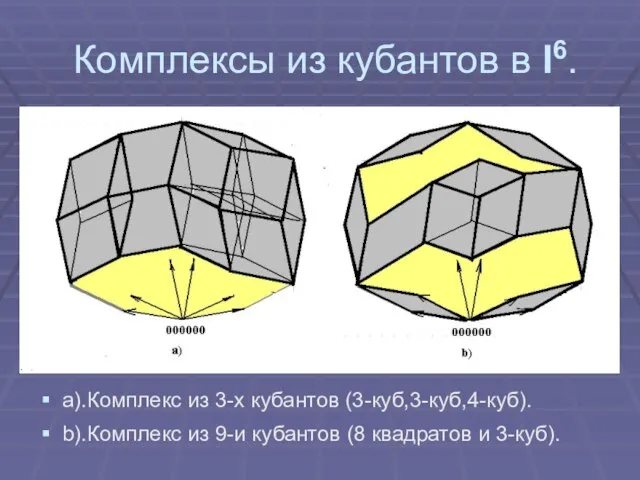
(8 квадратов и 3-куб).
Слайд 12Умножение (пересечение) кубантов.
Умножение кубантов- поразрядная операция над словами, задаваемая данной таблицей.
Ø-пустое множество.

Слайд 13Кубанты и псевдокубанты( с Ø) образуют полугруппу с единицей (моноид).
Расширение алфавита ?{Ø,0,1,2}.
Все

четверичные n-разрядные слова (кубанты и псевдокубанты) образуют полугруппу по умножению.
Кубант х кубант=кубант или п/кубант. П/кубант х кубант=п/кубант.
Единица моноида-кубант 222…2.
Слайд 14Машинное представление Ø?0;0?1;1?2;2?3;
Таблица поразрядного умножения элементов моноида при машинном представлении.

Слайд 15Свойства произведения кубантов.
П(D1,D2)=D3;
ω(D3) = число разрядов с Ø.
Если ω(D3)=0,то D3–кубант-пересечение.
Если ω(D3)= r>0,

то Lmin(D1,D2)=r; (минимальный путь по ребрам n-куба-обобщение метрики Хэмминга для двоичных кодов).
Структура комплекса полностью определяется перемножением кубантов.
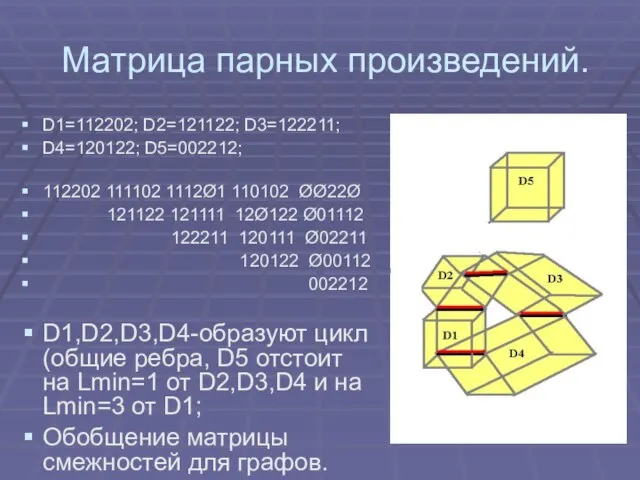
Слайд 16Матрица парных произведений.
D1=112202; D2=121122; D3=122211;
D4=120122; D5=002212;
112202 111102 1112Ø1 110102 ØØ22Ø
121122
121111 12Ø122 Ø01112
122211 120111 Ø02211
120122 Ø00112
002212
D1,D2,D3,D4-образуют цикл (общие ребра, D5 отстоит на Lmin=1 от D2,D3,D4 и на Lmin=3 от D1;
Обобщение матрицы смежностей для графов.
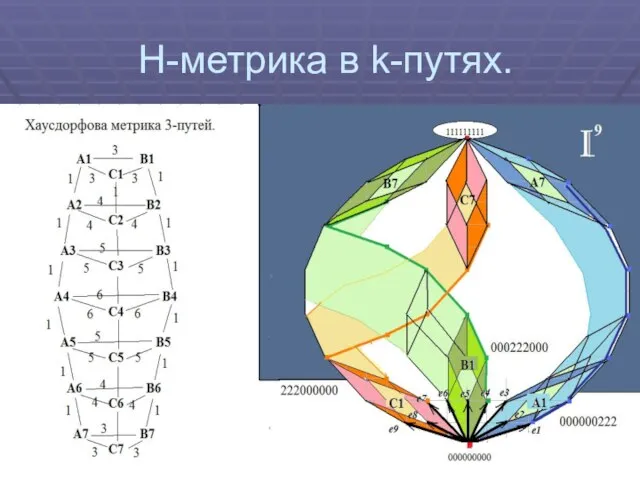
Слайд 17Хаусдорфова метрика на кубантах (обобщение метрики Хэмминга)
рН(D1,D2)=max{max minL(D1?D2),max minL(D2?D1)};
Хаусдорфово сжатие D1/D2=D1* и
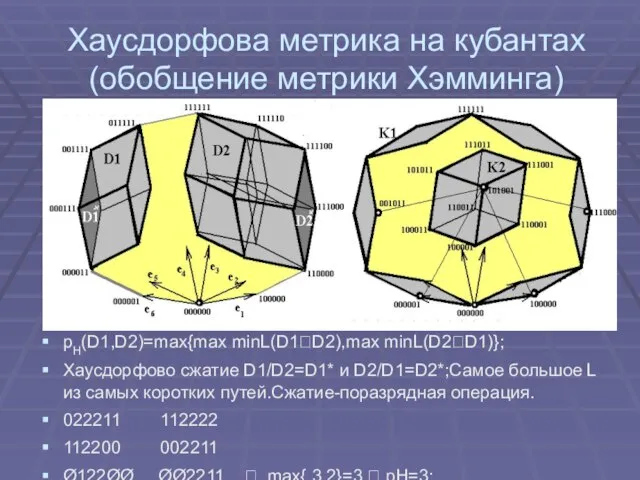
D2/D1=D2*;Cамое большое L из самых коротких путей.Сжатие-поразрядная операция.
022211 112222
112200 002211
Ø122ØØ ØØ2211 ? max{ 3,2}=3 ? pH=3;
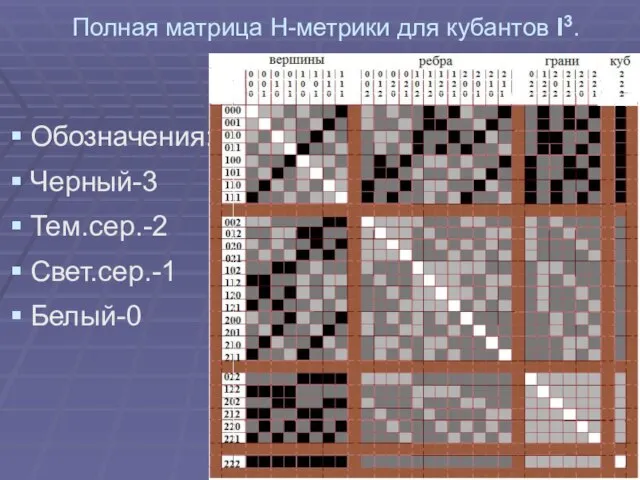
Слайд 18Полная матрица Н-метрики для кубантов I3.
Обозначения:
Черный-3
Тем.сер.-2
Свет.сер.-1
Белый-0
Слайд 19Структура матрицы Н-метрики для кубантов In.
Матрица 3nx3n
Миноры Н(k,m) k x m, где
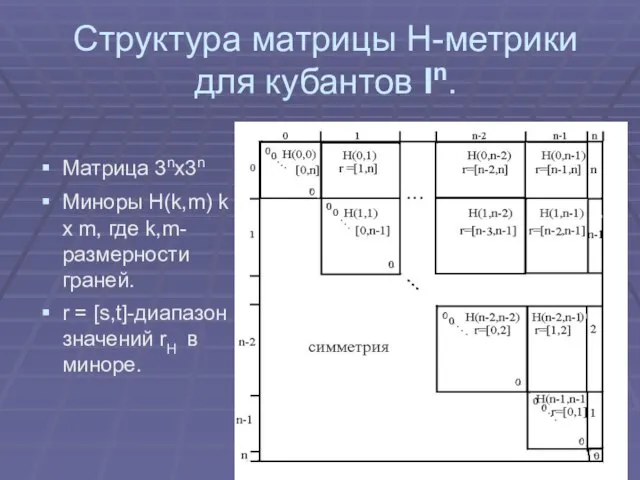
k,m- размерности граней.
r = [s,t]-диапазон значений rH в миноре.
Слайд 20Распределения значений Н-метрики по размерностям граней при n?∞.
Ассиметрия распределений.
r=0 ?
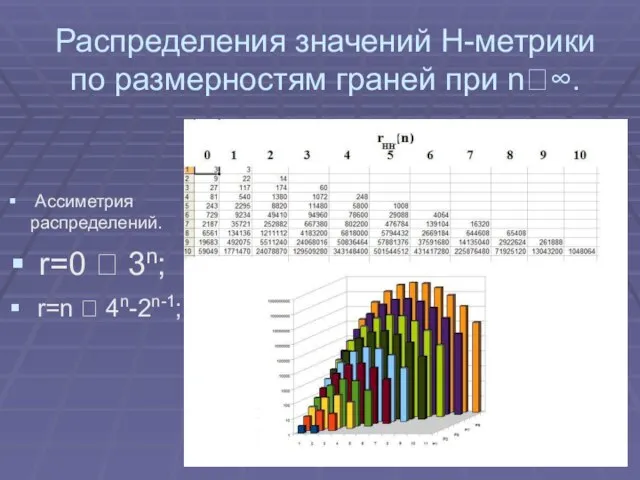
3n;
r=n ? 4n-2n-1;
Слайд 21Панельное топологическое строительство. Бутылка Клейна в 75 байт.
Всех комплексов из гиперграней
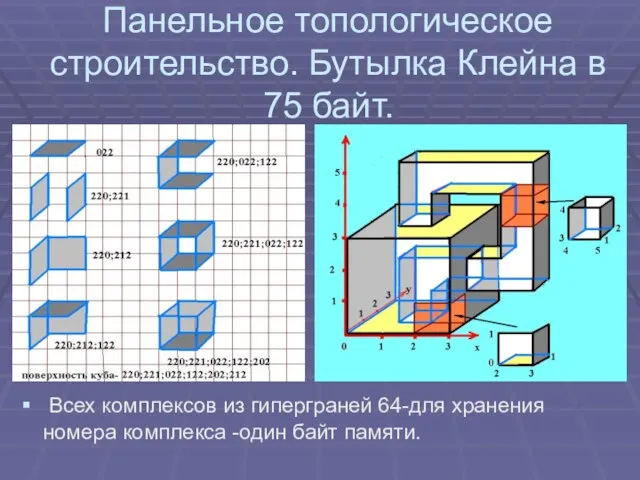
64-для хранения номера комплекса -один байт памяти.
Слайд 22Полиморфизм кубантов (четверичного кодирования).
Cлово
Число
Множество точек Rn.
Геометрическая фигура
Часть топологического комплекса.
Элемент алгебраической структуры (моноид).
Результат

одной операции содержит информацию о связности, мин пути, размерности пересечения, положении внутри n-куба.
Кубанты-гиперметрическое пространство.
Слайд 23Кубанты и супервычисления.
Поразрядные операции над четверичными словами практически неограниченной длины, равной размерности

исследуемого пространства.
Перевод вычисления метрики Хаусдорфа для кубантов из задач сложности 2n в задачи сложности n2.
Хранение в табличном виде (заранее рассчитанных) n-мерных комплексов гиперграней (нумеративный подход).
Исследования асимптотического поведения гиперрешеток (10d-11d) в интересах теоретической физики.
Одна из проблем-значительное расширение оперативной памяти суперкомпьютера.Для 10d рабочее поле со стороной 100 требует память объемом 108 терабайт.
Слайд 24Инструментальная система «Топологический процессор».
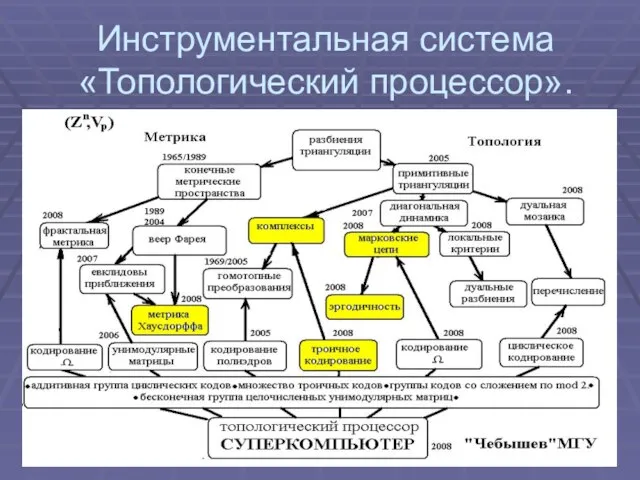
Слайд 25Вместо выводов.
Связка алгебраических геометрии и топологии, комбинаторики, дифференциальных уравнений со структурой будущих

суперкомпьютеров– одно из прорывных комплексных направлений не только в математике, но и в целом в науке.
Отечественная математическая школа в этой области - одна из передовых в мире.
Успех в этой области обеспечения суперкомпьютеров – шаг к занятию достойного места в международной научной кооперации.
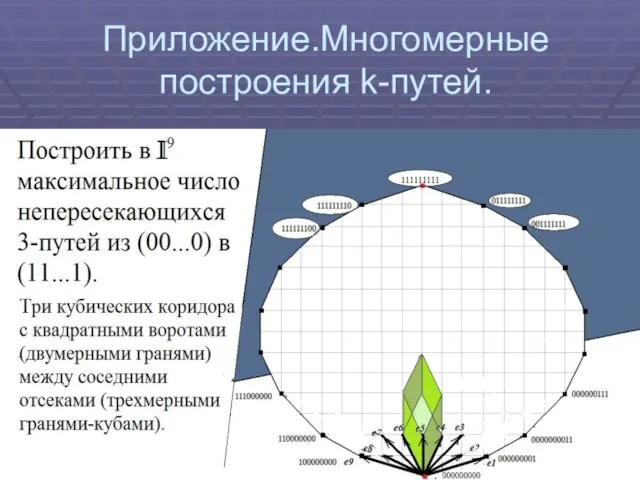
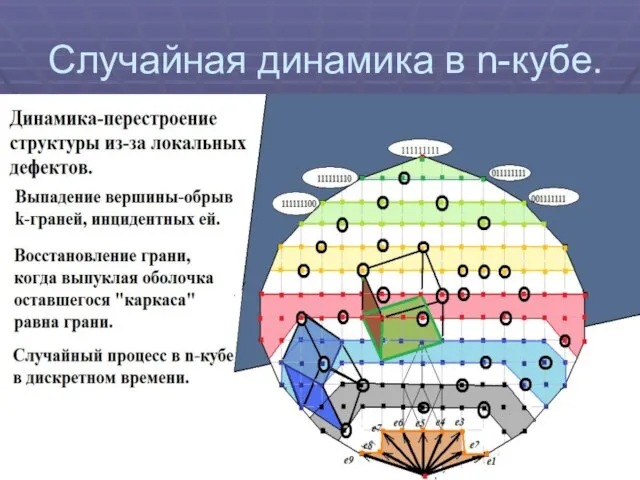
Слайд 26Приложение.Многомерные построения k-путей.
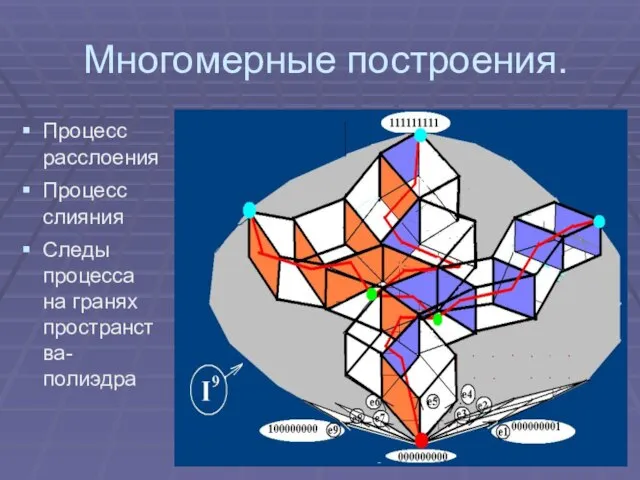
Слайд 29Многомерные построения.
Процесс расслоения
Процесс слияния
Следы процесса на гранях пространства-полиэдра
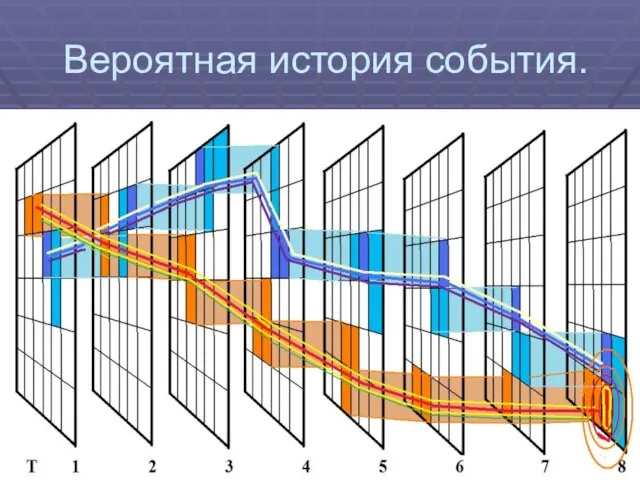
Слайд 313-пути (траектории) события (встречи).




























 Пиломатериалы, получение и применение
Пиломатериалы, получение и применение Совместное использование пакета Microsoft Office Excel 2007 и служб интеллектуального анализа данных SQL Server Analysis Services
Совместное использование пакета Microsoft Office Excel 2007 и служб интеллектуального анализа данных SQL Server Analysis Services Управление качеством
Управление качеством Стиль модерн и сопряжение
Стиль модерн и сопряжение «Удивительный мир многогранников»
«Удивительный мир многогранников» Промышленная Группа СОЮЗ. Многопрофильный холдинг, производитель полного спектра мебельных комплектующих для сборки мебели
Промышленная Группа СОЮЗ. Многопрофильный холдинг, производитель полного спектра мебельных комплектующих для сборки мебели Автономные энергетические системы на базе нетрадиционных источников энергии для горных поселений КР
Автономные энергетические системы на базе нетрадиционных источников энергии для горных поселений КР Модели и технологии обучения персонала розницы в период изменений
Модели и технологии обучения персонала розницы в период изменений Чрезвычайные ситуации техногенного характера
Чрезвычайные ситуации техногенного характера Тема проповеди: Виденье церковное – мое виденье
Тема проповеди: Виденье церковное – мое виденье Из конфликта в эффективную коммуникацию
Из конфликта в эффективную коммуникацию Политические режимы. Урок 3
Политические режимы. Урок 3 Зрительное восприятие цвета
Зрительное восприятие цвета Стратегия развития современных технологий мобильной связи на Дальнем Востоке и в Восточной Сибири
Стратегия развития современных технологий мобильной связи на Дальнем Востоке и в Восточной Сибири Сачки и дезертиры
Сачки и дезертиры Художественные образы СПБ: российский город на перекрёстке мировых культур
Художественные образы СПБ: российский город на перекрёстке мировых культур Фактори забезпечення конкурентоспроможності підприємства
Фактори забезпечення конкурентоспроможності підприємства Три клада у Природы есть:вода,Земля и воздух – три ее основы.Какая бы ни грянула беда,Целы они – все возродится снова.
Три клада у Природы есть:вода,Земля и воздух – три ее основы.Какая бы ни грянула беда,Целы они – все возродится снова. Конвейер проектов. Критерии и роли. Специфика выполнения
Конвейер проектов. Критерии и роли. Специфика выполнения Проектно-изыскательские работы. Градостроительная документация. Лекция 1
Проектно-изыскательские работы. Градостроительная документация. Лекция 1 Добыча нефти
Добыча нефти Презентация на тему Правописание падежных окончаний имен существительных единственного числа (4 класс)
Презентация на тему Правописание падежных окончаний имен существительных единственного числа (4 класс) THE PRESENT PERFECT TENSE НАСТОЯЩЕЕ СОВЕРШЕННОЕ ВРЕМЯ
THE PRESENT PERFECT TENSE НАСТОЯЩЕЕ СОВЕРШЕННОЕ ВРЕМЯ Кобелев Н.Б.ВЗФЭИ, Москва
Кобелев Н.Б.ВЗФЭИ, Москва Театрально-игровая деятельность - как средство развития творческих способностей детей дошкольного возраста
Театрально-игровая деятельность - как средство развития творческих способностей детей дошкольного возраста Презентация на тему Частица как служебная часть речи.
Презентация на тему Частица как служебная часть речи.  Спасенный сад
Спасенный сад Караоке-баттл 99 баллов. Описание игры
Караоке-баттл 99 баллов. Описание игры