Помехоустойчивое кодирование

Для защиты полезной информации необходимо вводить избыточность (смысловая, физическая, статистическая, )
Коды, позволяющие обнаруживать и исправлять ошибки бывают двух видов:
блоковые коды;
сверточные коды
Коды, которые обеспечивают возможность обнаружения и исправления ошибки, называют помехоустойчивыми.
Код, содержащий помимо информационных еще и контрольные разряды называется систематическим кодом.
Длина слова систематического кода (n) =
число информационных разрядов (m) + число контрольных разрядов(k)

Надежность обеспечивается тем, что наряду с битами, непосредственно кодирующими сообщение (будем называть их информационными битами), передаются (хранятся) дополнительные биты, по состоянию которых можно судить о правильности передачи (будем называть их контрольными битами). При равномерном кодировании* сообщения длина кодовой цепочки на знак (или группу знаков) n складывается из длины информационной части m и числа контрольных битов k. Очевидно, n ≥m .
Подобно введенной ранее величине Q, характеризующей относительную избыточность кода при передаче по идеальному каналу, в рассматриваемом случае удобно определить избыточность сообщения для реального канала L следующим образом:
(1)
Относительная избыточность сообщения - это характеристика, показывающая, во сколько раз требуется удлинить сообщение, чтобы обеспечить его надежную (безошибочную) передачу (хранение).
Очевидно, что L характеризует эффективность кодирования при передаче по реальным каналам и при равных надежностях передачи предпочтение должно быть отдано тому способу кодирования, при котором избыточность окажется наименьшей. Правда, для практики важна также простота технической реализации того или иного способа кодирования.

Задача обнаружения ошибки может быть решена довольно легко. Достаточно передавать каждую букву сообщения дважды.
Например, при необходимости передачи слова «гора» можно передать «ггоорраа».
При получении искаженного сообщения, например, «гготрраа» с большой вероятностью можно догадаться, каким было исходное слово. Конечно, возможно такое искажение, которое делает неоднозначным интерпретацию полученного сообщения, например, «гпоорраа», «ггоорреа» или «кгоорраа».
Однако цель такого способа кодирования состоит не в исправлении ошибки, а в фиксации факта искажения и повторной передаче части сообщения в этом случае. Недостаток данного способа обеспечения надежности состоит в том, что избыточность сообщения оказывается очень большой - очевидно, L = 2.
Поскольку ошибка должна быть только обнаружена, можно предложить другой способ кодирования. Пусть имеется цепочка информационных бит длиной m. Добавим к ним один контрольный бит (k = 1), значение которого определяется тем, что новая кодовая цепочка из m + 1 бит должна содержать четное количество единиц - по этой причине такой контрольный бит называется битом четности.
Коды, обнаруживающие ошибку

Например, для информационного байта 01010100 бит четности будет иметь значение 1, а для байта 11011011 бит четности равен 0.
В случае одиночной ошибки передачи число 1 перестает быть четным, что и служит свидетельством сбоя. Например, если получена цепочка 110110111 (контрольный бит выделен подчеркиванием), ясно, что передача произведена с ошибкой, поскольку общее количество единиц равно 7, т.е. нечетно.
Предложенный способ кодирования не позволяет установить, в каком конкретно бите содержится ошибка и, следовательно, не дает возможности ее исправить. Избыточность сообщения при этом равна:
На первый взгляд кажется, что путем увеличения m можно сколь угодно приближать избыточность к ее минимальному значению (Lmin = 1). Однако с ростом m,
во-первых, растет вероятность парной ошибки, которая контрольным битом не отслеживается;
во-вторых, при обнаружении ошибки потребуется заново передавать много информации. Поэтому обычно m = 8 или 16 и, следовательно, L = 1,125 (1,0625).

Можно было бы предложить простой способ установления ошибки – передавать каждый символ трижды, например, «гггооорррааа» – тогда при получении сообщения «гггооопррааа» ясно, что ошибочной оказывается буква «п» и ее следует заменить на «р».
Безусловно, при этом предполагается, что вероятность появления парной ошибки невелика. Такой метод кодирования приводит к избыточности сообщения L = 3, что неприемлемо с экономической точки зрения.
Прежде, чем обсуждать метод кодирования, позволяющий локализовать и исправить ошибку передачи, произведем некоторые количественные оценки.
Наличие шумов в канале связи ведет к частичной потере передаваемой информации на величину возникающей неопределенности, которая при передаче одного бита исходного сообщения составляет
где р - вероятность появления ошибки в сообщении. Для восстановления информационного содержания сообщения следует дополнительно передать количество информации не менее величины ее потерь, т.е. вместо передачи каждого 1 бит информации следует передавать 1 + Н бит. В этом случае избыточность сообщения составит
Коды, исправляющие одиночную ошибку
(2)

Приведенную избыточность следует считать минимальной (это указывает ее индекс), поскольку при передаче сообщения по каналу, характеризуемому вероятностью искажения р, при избыточности, меньшей Lmin восстановление информации оказывается невозможным.
Пример
Какое минимальное количество контрольных бит должно передаваться вместе с 16-ю информационными для обеспечения восстановимости информации, если вероятность искажения составляет 1%?
Подставляя р = 0,01 в (2), находим Lmin ≈ 1,081. При m = 16 из (1) получаем n = m ∙ Lmin = 17,29. Следовательно, с учетом того, что количество контрольных бит выражается целым числом, k ≥ n - m = 2. Реальная избыточность согласно (1) составит L = 1,125.
Выражение (2) устанавливает границу избыточности, при которой возможно восстановление переданной информации, однако, не указывает, каким образом следует осуществить кодирование, чтобы ошибка могла быть локализована (т.е. определено, в каком бите она находится) и, естественно, устранена.

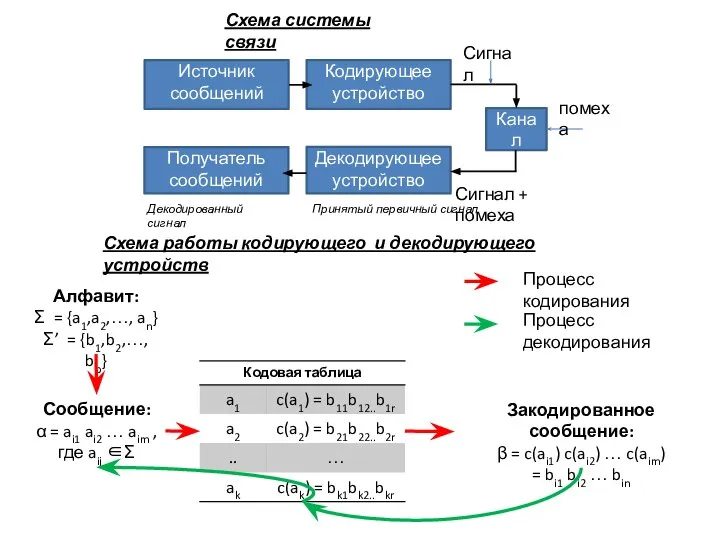
Источник сообщений
Кодирующее устройство
Канал
Получатель сообщений
Декодирующее устройство
Сигнал
Сигнал + помеха
Принятый первичный сигнал
Декодированный сигнал
помеха
Схема системы связи
Сообщение:
α = ai1 ai2 … aim ,
где aij ∈Σ
Алфавит:
Σ = {a1,a2,…, an}
Σ’ = {b1,b2,…, bp}
Закодированное сообщение:
β = c(ai1) c(ai2) … c(aim)
= bi1 bi2 … bin
Схема работы кодирующего и декодирующего устройств
Процесс кодирования
Процесс декодирования

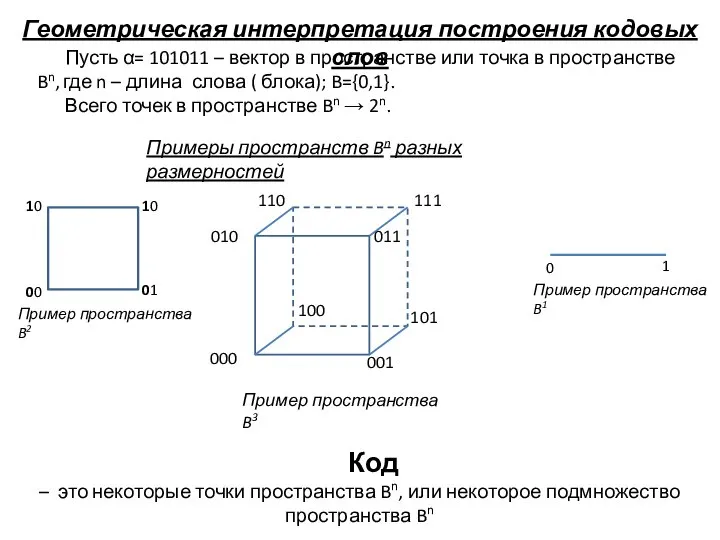
Геометрическая интерпретация построения кодовых слов
Пусть α= 101011 – вектор в пространстве или точка в пространстве Bn, где n – длина слова ( блока); B={0,1}.
Всего точек в пространстве Bn → 2n.
Пример пространства B3
Код
– это некоторые точки пространства Bn, или некоторое подмножество пространства Bn
Пример пространства B2
00
01
10
10
Пример пространства B1
0
1
Примеры пространств Bn разных размерностей

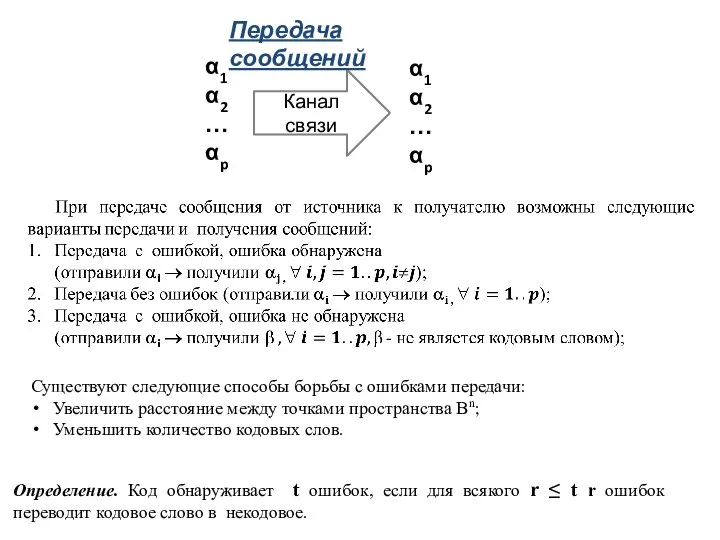
α1
α2
…
αp
Канал связи
α1
α2
…
αp
Передача сообщений
Существуют следующие способы борьбы с ошибками передачи:
Увеличить расстояние между точками пространства Bn;
Уменьшить количество кодовых слов.
Определение. Код обнаруживает t ошибок, если для всякого r ≤ t r ошибок переводит кодовое слово в некодовое.

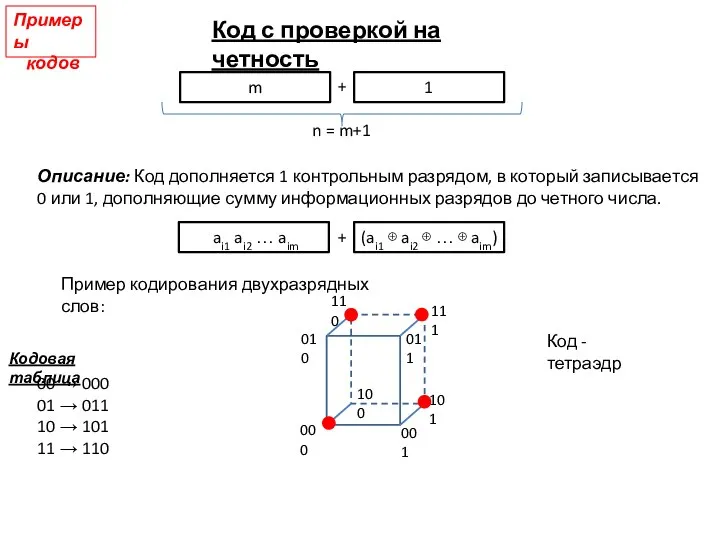
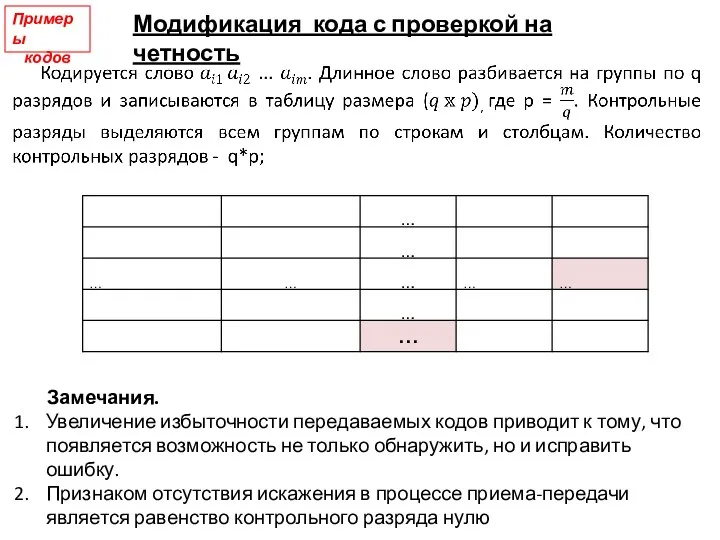
Код с проверкой на четность
m
1
n = m+1
Описание: Код дополняется 1 контрольным разрядом, в который записывается 0 или 1, дополняющие сумму информационных разрядов до четного числа.
ai1 ai2 … aim
(ai1 ⊕ ai2 ⊕ … ⊕ aim)
+
+
Пример кодирования двухразрядных слов:
00 → 000
01 → 011
10 → 101
11 → 110
Код -тетраэдр
Примеры
кодов
Кодовая таблица

Примеры
кодов
Замечания.
Увеличение избыточности передаваемых кодов приводит к тому, что появляется возможность не только обнаружить, но и исправить ошибку.
Признаком отсутствия искажения в процессе приема-передачи является равенство контрольного разряда нулю
Модификация кода с проверкой на четность

Примеры кодов
Один заданный информационный символ повторяется n раз. Это (n, 1)-код. Для него минимальное расстояние равно n, и при предположении, что большинство принятых битов совпадает с переданным информационным битом, может быть исправ­лено (n — 1)/2 ошибок.
Коды с повторением

Определение: Минимальное расстояние, взятое по всем парам кодовых разрешенных комбинаций кода, называют (минимальным) кодовым расстоянием (d0min).
Расстояние Хэмминга. Кодовое расстояние
0110100
0010101
0100001
⊕
Пример: Рассмотрим код, заданный таблицей
d0min = 2
– кодовое расстояние для данного кода

При взаимно независимых ошибках наиболее вероятен переход в кодовую комбинацию, отличающуюся от данной в наименьшем числе символов.
Рассмотрим код, исправляющий ошибку. Идея построения такого кода наглядно иллюстрируется геометрической моделью трехзначного двоичного кода на все сочетания, которая представляет собой куб.
Для каждой вершины куба имеются три вершины, которые отстоят от нее на один шаг (на расстоянии одного ребра куба), еще три вершины, которые отстоят на два шага, и одна вершина — на три шага.
Расстояние между ближайшими кодовыми комбинациями называется кодовым расстоянием.
Замечание. Кодовое расстояние — параметр, характеризующий помехоустойчивость кода и заложенную в нем избыточность.
Геометрическая интерпретация кодового расстояния и расстояния Хэмминга

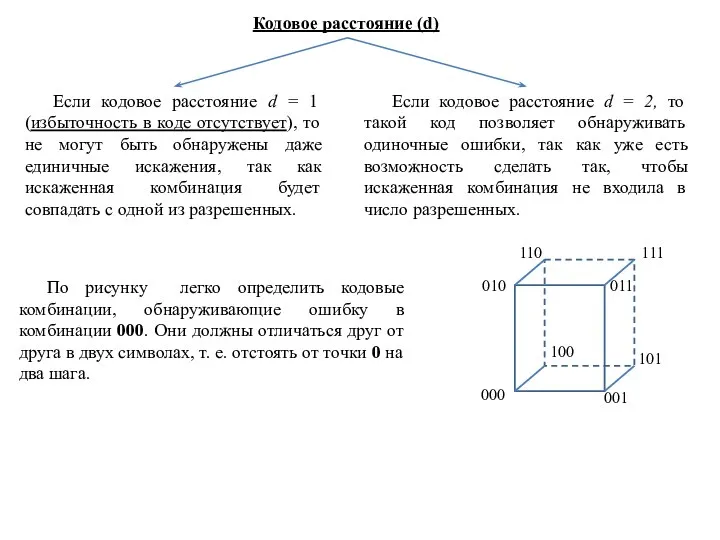
Кодовое расстояние (d)
Если кодовое расстояние d = 1 (избыточность в коде отсутствует), то не могут быть обнаружены даже единичные искажения, так как искаженная комбинация будет совпадать с одной из разрешенных.
Если кодовое расстояние d = 2, то такой код позволяет обнаруживать одиночные ошибки, так как уже есть возможность сделать так, чтобы искаженная комбинация не входила в число разрешенных.
По рисунку легко определить кодовые комбинации, обнаруживающие ошибку в комбинации 000. Они должны отличаться друг от друга в двух символах, т. е. отстоять от точки 0 на два шага.

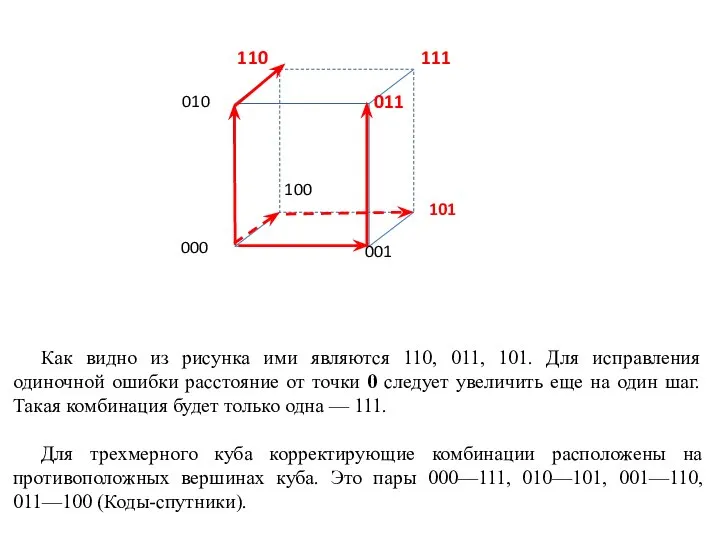
Как видно из рисунка ими являются 110, 011, 101. Для исправления одиночной ошибки расстояние от точки 0 следует увеличить еще на один шаг. Такая комбинация будет только одна — 111.
Для трехмерного куба корректирующие комбинации расположены на противоположных вершинах куба. Это пары 000—111, 010—101, 001—110, 011—100 (Коды-спутники).

Идея исправления ошибки в кодах-спутниках весьма проста. Главное, чтобы при искажении любой комбинации не могла быть образована соседняя рабочая комбинация. Процесс исправления ошибки заключается в том, что искаженная комбинация отождествляется с ближайшей разрешенной комбинацией.
Например, если передавать буквы алфавита, которым соответствуют следующие комбинации двоичного кода: А — 00000, Б — 00111 и В — 11100, то при искажении любого одного знака легко определить, какая комбинация была передана, так как каждая из них отличается друг от друга не меньше чем в трех символах (кодовое расстояние d ≥ 3).
Исправление ошибки в кодах-спутниках

В общем случае при необходимости обнаруживать ошибки кратности до r включительно минимальное хэммингово расстояние между разрешенными кодовыми комбинациями должно быть по крайней мере на единицу больше r.
В общем случае для обеспечения возможности исправления всех ошибок кратности до s включительно при декодировании по методу максимального правдоподобия, каждая из ошибок должна приводить к запрещенной комбинации, относящейся к подмножеству исходной разрешенной кодовой комбинации
Декодирование после приема производится таким образом, что принятая кодовая комбинация отождествляется с той разрешенной, которая находится от нее на наименьшем кодовом расстоянии.
Такое декодирование называется декодированием по методу максимального правдоподобия
d0 min≥r+1

Пример. Рассмотрим (2,3)–код с проверкой на четность. Множество кодовых слов есть 000, 101, 011, 110. Минимальное расстояние между кодовыми словами равно 2. Этот код способен обнаруживать однократную ошибку.
Общее выражение для определения кодового расстояния в случае одновременного обнаружения и исправления ошибок
d = r + s + 1
, где
r — число обнаруживаемых ошибок;
s — число исправляемых ошибок;
d — минимальное количество элементов, в которых одна кодовая комбинация отличается от другой.
Если требуется определить кодовое расстояние исходя только из количества исправляемых ошибок, то применяют формулу
d = 2s + 1

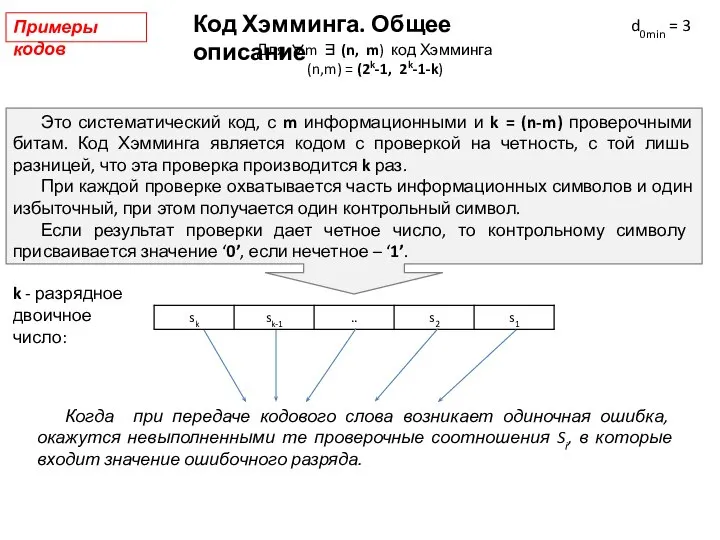
Код Хэмминга. Общее описание
d0min = 3
Когда при передаче кодового слова возникает одиночная ошибка, окажутся невыполненными те проверочные соотношения Si, в которые входит значение ошибочного разряда.
Примеры кодов
Для ∀m ∃ (n, m) код Хэмминга
(n,m) = (2k-1, 2k-1-k)
k - разрядное двоичное число:
Это систематический код, с m информационными и k = (n-m) проверочными битам. Код Хэмминга является кодом с проверкой на четность, с той лишь разницей, что эта проверка производится k раз.
При каждой проверке охватывается часть информационных символов и один избыточный, при этом получается один контрольный символ.
Если результат проверки дает четное число, то контрольному символу присваивается значение ‘0’, если нечетное – ‘1’.

Порядок кодирования по методу Хемминга

и
Зависимость между числом информационных и проверочных разрядов
Соотношение между количеством информационных и контрольных символов в коде Хэмминга

Пример. Матрица кода Хэмминга (15,11)
Определение мест расположения и значений контрольных символов
Строки матрицы – это проверочные уравнения из которых вычисляются значения контрольных разрядов. Единицы в строке – обозначают разряды, которые будут принимать участие в суммировании (или в контролировании).
Для определения мест расположения контрольных символов необходимо построить матрицу кода Хемминга. Размер матрицы - (k*n).
Характерной её особенностью является то, что столбцы матрицы являются различными ненулевыми комбинациями символов алфавита {0,1} длины k, выписанные в порядке возрастания их значений.
k
n=2k
s1 = u’1⊕u’3⊕u’5⊕u’7⊕u’9⊕u’11⊕u’13⊕u’15 = 0
s2 = u’2⊕u’3⊕u’6⊕u’7⊕u’10⊕u’11⊕u’14⊕u’15 = 0
s3 = u’4⊕u’5⊕u’6⊕u’7⊕u’12⊕u’13⊕u’14⊕u’15 = 0
s4 = u’8⊕u’9⊕u’10⊕u’11⊕u’12⊕u’13⊕u’14⊕u’15 =0
(*)

Целесообразно выбирать такое размещение контрольных символов в кодовой комбинации, при которой каждый из них включается в минимальное число проверяемых групп (лучше в одну). На этом основании контрольные разряды это
– u’1, u’2, u’4, u’8 , то есть те места, где столбцы матрицы Хэмминга является степенью числа 2 - 20, 21, 22, 24 и т.д.
Пример. Матрица кода Хэмминга (15,11)
Окончательно получаем закодированное сообщение для кода (15,11):
Значения контрольных разрядов получаем из системы уравнений (*):
k1 = u’3⊕u’5⊕u’7⊕u’9⊕u’11⊕u’13⊕u’15
k2 = u’3⊕u’6⊕u’7⊕u’10⊕u’11⊕u’14⊕u’15
k3 = u’5⊕u’6⊕u’7⊕u’12⊕u’13⊕u’14⊕u’15
k4 = u’9⊕u’10⊕u’11⊕u’12⊕u’13⊕u’14⊕u’15

Порядок проведения проверок и декодирования
При получении закодированного по методу Хэмминга сообщения необходимо проверить выполнимость соотношений для контрольных разрядов:
s1 = k1⊕u’3⊕u’5⊕u’7⊕u’9⊕u’11⊕u’13⊕u’15
s2 = k2⊕u’3⊕u’6⊕u’7⊕u’10⊕u’11⊕u’14⊕u’15
s3 = k3⊕u’5⊕u’6⊕u’7⊕u’12⊕u’13⊕u’14⊕u’15
s4 = k4⊕u’9⊕u’10⊕u’11⊕u’12⊕u’13⊕u’14⊕u’15
В результате будет получена k-разрядное число S, которое называется «синдром»:
S:
Правила интерпретации значения синдрома:
S=0 – передача сообщения произошла без ошибок;
S<>0 – во время передачи произошла ошибка, при этом – десятичное значение синдрома – номер разряда , переданного с ошибкой.

Алгоритм декодирования кода Хэмминга:
Провести проверку всех битов чётности
Если все биты чётности верны, то перейти к п 5.
Вычислить сумму номеров всех неправильных битов чётности
Инвертировать содержимое бита, номер которого равен сумме, найденной в п.3
Исключить биты чётности , передать правильный информационный код

Пример: Закодировать сообщение 1101 кодом Хэмминга.
m=4, k=3,n=7
0 0 0 1 1 1 1
H = 0 1 1 0 0 1 1
1 0 1 0 1 0 1
В качестве проверенных разрядов выбираем 1й, 2й и 4й. Чтобы закодировать сообщение 1101, нужно определить проверочные разряды в комбинации
[k1 k2 1 k3 1 0 1]. Из матрицы H получаем:
k1 = u3⊕u5⊕u7
k2 = u3⊕u6⊕u7
k3 = u5⊕u6⊕u7
Следовательно, k1 = 1, k2 = 0, k3 = 0 и закодированное сообщение имеет вид: 1010101.
Предположим, что шестой символ принят ошибочно, тогда будет получено сообщение 1010111. Синдром в этом случае имеет вид 110. т. е. двоичное представление числа 6.

Для обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядов m и числом корректирующих разрядов k должно удовлетворять следующим условиям:
При этом подразумевается, что общая длина кодовой комбинации n = m + k
Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием d0min = 3 удобно пользоваться выражениями:
Если известна длина полной кодовой комбинации n
2. Если при расчетах удобнее исходить из заданного числа информационных символов m
При построении кодов перед разработчиками стоит задача определения числа добавочных, корректирующих символов k, или исходя из числа информационных разрядов m, либо из общей длины кода n.

Для кодов, обнаруживающих все трехкратные ошибки (d0min = 4)
Для кодов длиной в n символов, исправляющих одну или две ошибки (d0min = 5),
Для практических расчетов можно пользоваться выражением
Для кодов, исправляющих три ошибки (d0min = 7),

Для кодов, исправляющих S ошибок (d0min = 2S + 1),
В настоящее время разработаны десятки кодов, которые теоретически могут обнаруживать произвольное количество ошибок.
Выражение слева известно как нижняя граница Хэмминга, а выражение справа как верхняя граница Варшамова — Гильберта.