Понятие о решетчатой функции и её разности

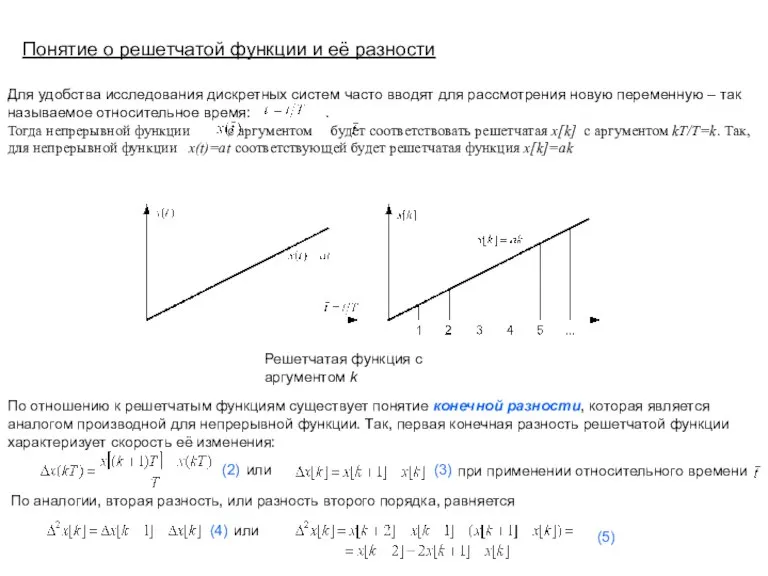
Для удобства исследования дискретных систем часто вводят для рассмотрения новую переменную – так называемое относительное время: .
Тогда непрерывной функции с аргументом будет соответствовать решетчатая x[k] с аргументом kT/T=k. Так, для непрерывной функции x(t)=at соответствующей будет решетчатая функция x[k]=ak
Решетчатая функция с аргументом k
Понятие о решетчатой функции и её разности
По отношению к решетчатым функциям существует понятие конечной разности, которая является аналогом производной для непрерывной функции. Так, первая конечная разность решетчатой функции характеризует скорость её изменения:
или
при применении относительного времени
По аналогии, вторая разность, или разность второго порядка, равняется
или
(3)
(4)
(5)
(2)

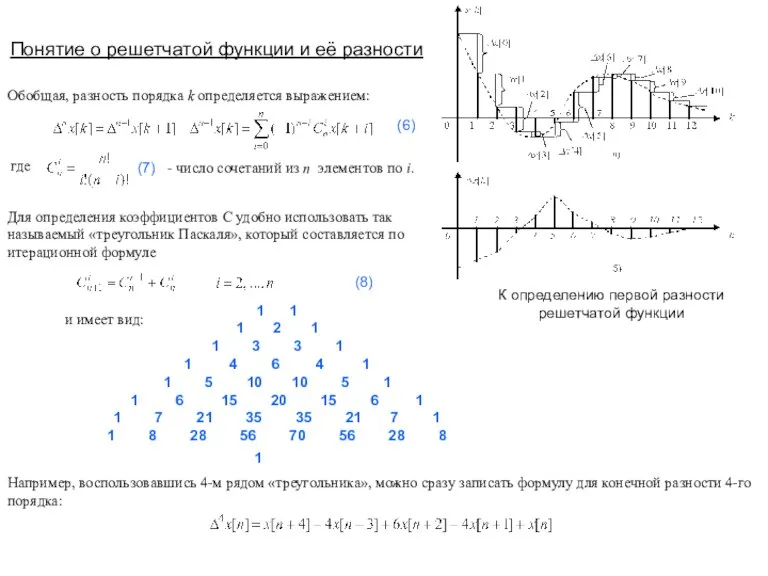
Понятие о решетчатой функции и её разности
К определению первой разности
решетчатой функции
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Обобщая, разность порядка k определяется выражением:
где
- число сочетаний из n элементов по i.
Для определения коэффициентов C удобно использовать так называемый «треугольник Паскаля», который составляется по итерационной формуле
и имеет вид:
Например, воспользовавшись 4-м рядом «треугольника», можно сразу записать формулу для конечной разности 4-го порядка:
(6)
(7)
(8)

Разностные уравнения. Связь между разностными уравнениями и дискретными передаточными функциями
Для исследования дискретных САР используются так называемые разностные уравнения, которые определяют взаимосвязь между решетчатой функцией и её разностями:
Оператор ∆ для дискретной функции является своеобразным аналогом оператора дифференцирования D=d/dt для непрерывной функции:
Это выражение можно использовать для нахождения аналога линейного ДУ в виде разностного.
Если в уравнение (9) подставить выражение для конечных разностей (6), то получим неоднородное линейное разностное уравнение, которое определяет зависимость между значениями решетчатой функции в разные дискретные моменты времени
Учитывая, что дискретный оператор z связан с непрерывным оператором Лапласа p выражением:
то для перехода от разностного уравнения в области времени в виде (11) к соответствующему уравнению в области оператора z изображения сигналов, которые опережают сигнал в текущий момент времени x[k] на i тактов, умножаются на zi, а изображения сигналов, которые запаздывают относительно этого сигнала на i тактов – умножаются на z-і, то есть
(9)
(10)
(11)
(13)
(14)

По таким правилам уравнение (11) преобразуется к виду
откуда легко определяется дискретная передаточная функция (ДПФ) импульсной системы в полиномиальной форме как отношение изображений выходного сигнала к входному при нулевых начальных условиях
условием физической реализации передаточной функции ДПФ является m≤n, т.е., степень полинома числителя не должна превышать степень полинома знаменателя. Если это условие не выполняется, это означает, что выходной сигнал опережает входной, что невозможно с диалектической точки зрения.
Разностные уравнения. Связь между разностными уравнениями и дискретными передаточными функциями
Полином Gn(z) в знаменателе ДПФ называется характеристическим полиномом (Denominator), ур-ние
– характеристическим уравнением, а его корни
– дискретными полюсами (Poles), или собственными числами (Eigen Value) системы.
Полином Hm(z) в числителе ДПФ называют полиномом воздействия (Numerator). Корни уравнения
называются дискретными нулями (Zeros):
(15)
(16)

Условие устойчивости дискретной системы может быть сформулировано так: дискретная САР будет устойчивой, если корни её характеристического уравнения, изображенные на комплексной z-плоскости, лежат внутри окружности единичного радиуса, или по модулю меньше единицы.
Карта полюсов устойчивой
дискретной САР
Разностные уравнения. Связь между разностными уравнениями и дискретными передаточными функциями
Свободное движение системы будет устойчивым при условии
поскольку только при таких условиях его решение будет сходится
Пример
Получить разностное уравнение и дискретную передаточную функцию из дифференциального уравнения непрерывного объекта:
сравнить переходные функции непрерывного и соответствующего дискретного объектов при разных периодах дискретизации, проанализировать устойчивость дискретной системы.
Решение.
После подстановки в последнее равенство выражений для конечных разностей (3)-(5), получаем:
или, после упрощения:
(18)

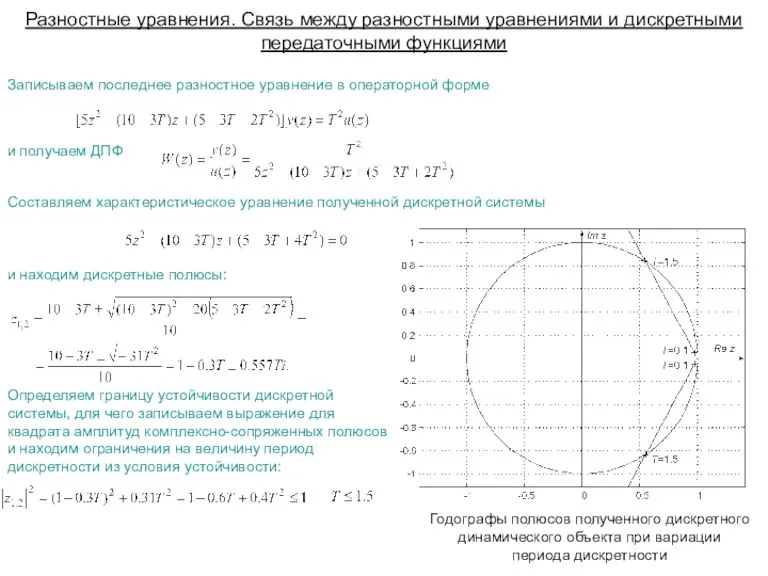
Записываем последнее разностное уравнение в операторной форме
и получаем ДПФ
Составляем характеристическое уравнение полученной дискретной системы
и находим дискретные полюсы:
Определяем границу устойчивости дискретной системы, для чего записываем выражение для квадрата амплитуд комплексно-сопряженных полюсов и находим ограничения на величину период дискретности из условия устойчивости:
Годографы полюсов полученного дискретного
динамического объекта при вариации периода дискретности
Разностные уравнения. Связь между разностными уравнениями и дискретными передаточными функциями

sa=tf(1,[5 3 2])
step(sa), grid on, hold on
for T=[0.25 1]
sd=tf(T^2,[5 -10+3*T 5-3*T+2*T^2],T) step(sd)
end
Чтобы сравнить переходные характеристики выходной непрерывной системы и её дискретной аппроксимации воспользуемся Simulink-моделью
Без использования Simulink:
Разностные уравнения. Связь между разностными уравнениями и дискретными передаточными функциями

Дискретное преобразование Лапласа
Как известно, непрерывная функция времени x(t) при одностороннем преобразовании Лапласа отображается в функцию комплексной переменной x(p):
(19)
– комплексная переменная
где
Для решетчатых функций таким же способом вводится понятие дискретного преобразования Лапласа:
где D – символ дискретного преобразования,
x*(p) – функция, которая получена в результате дискретного преобразования решетчатой функции x(kT).
Если ввести к рассмотрению относительное время, имеем:
(20)
или, при использовании новой безразмерной переменной q=pT:
(21)
(22)
Пример Найти дискретное преобразование Лапласа для единичной решетчатой функции x[k]=1[k].
Решение. В соответствии с выражением (20) находим:
Используя известную формулу для суммы элементов геометрической прогрессии, окончательно имеем

Основные свойства дискретного преобразования Лапласа:
Дискретное преобразование Лапласа
1) поскольку дискретное преобразование Лапласа определяет связь между функцией и её изображением только в моменты t=nT, то разным выходным функциям x(t), которые совпадают в эти моменты времени, будет соответствовать одна и та же функция x*(p). Итак, невозможно однозначно восстановить функцию x(t) из x*(p) для произвольного момента времени t.
2) легко доказать, что функция x*(p) является периодической вдоль мнимой оси jω комплексной плоскости, а её период составляет ωs=2π/T. Если принять, что i – произвольное целое число, то математически это свойство дискретного преобразования Лапласа можно записать так:
3) функция x*(p) является иррациональной относительно p, поскольку содержит множители типа e-pT. Это существенно отличает её от большинства непрерывных функций.

Z- преобразование и его свойства
Для исследования свойств цифровых систем широко используется и так называемое Z- преобразование, которое следует из дискретного преобразования Лапласа при
Итак, по аналогии с дискретным преобразованием, можем записать:
Так, для задачи из примера Z- преобразование заданной единичной решетчатой функции будет
Обозначим некоторые свойства Z- преобразования:
1) условием существования функции x(z) есть определенность функции x(t) для всех моментов времени t=kT;
2) функция x(z) является рациональной относительно комплексной переменной z;
3) для какой-нибудь функции времени x(t), которая имеет дискретное преобразование Лапласа, существует и Z- преобразование;
4) одной функции x(z) соответствует множество функций времени x(t), которые совпадают только в моменты времени t=kT;
5) преобразование z=epT отображает всю левую полуплоскость комплексной плоскости p в круг единичного радиуса на комплексной плоскости z с центром в начале координат;
6) свойство суперпозиции:
7) свойство линейности:
(23)
(24)

8) свойство сдвига во времени (запаздывание и опережение):
Z- преобразование и его свойства
9) свертке оригиналов соответствует произведение изображений:
10) теорема о граничном значении:
11) дифференцирование изображения:
12) Z- преобразование функции не зависит от величины T. Действительно, поскольку время не входит в выражение (24), то выражение для x(z) не зависит от величины T.

При вычислении Z- преобразования функций удобно исходить не с функции времени x(t), а из его преобразования Лапласа, т.е. x(p). Рассмотрим пример такого вычисления Z- преобразования функции.
Z- преобразование и его свойства
Пример 3. Найти Z- преобразование функции
Решение. Как известно, преобразованием Лапласа заданной функции есть функция комплексной переменной
Одновременно, согласно (20),
Находим сумму этой геометрической прогрессии:
Поскольку
, окончательно получим:
Таким же способом можно получить дискретное преобразование Лапласа и Z- преобразование для других функций.

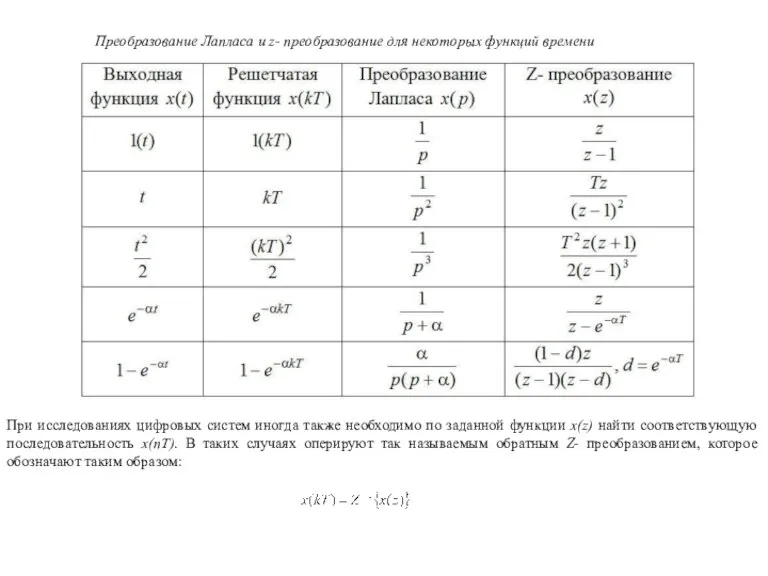
Преобразование Лапласа и z- преобразование для некоторых функций времени
При исследованиях цифровых систем иногда также необходимо по заданной функции x(z) найти соответствующую последовательность x(nT). В таких случаях оперируют так называемым обратным Z- преобразованием, которое обозначают таким образом:

Как вычислять z-преобразование
Matlab
syms k
x = 1 + 2^(k+1);
X = ztrans ( x );
X = combine ( X )
X =
(3*z^2–4*z)/(z^2–3*z+2)
упрощение
z-преобразование

Обратное z-преобразование (численно)
Matlab
n = [3 -4 0];
d = [1 -3 2];
T = 1;
X = tf( n, d, T);
x = impulse(X, 4)
x = 3
5
9
17
33
конечное время