Понятие вероятности

Статистическое определение вероятности
Вероятность как предельное значение частоты.

Самостоятельная работа

Ошибка Даламбера.
Великий французский философ и математик Даламбер вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!
Жан Лерон Даламбер
(1717 -1783)

Ошибка Даламбера.
Опыт. Подбрасываем две одинаковые монеты. Какова вероятность того, что они упадут на одну и ту же сторону?
Решение Даламбера:
Опыт имеет три
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) одна из монет упадет на «орла», другая на «решку».
Из них благоприятными
будут два исхода.
Правильное решение:
Опыт имеет четыре
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) первая монета упадет на «орла», вторая на «решку»;
4) первая монета упадет на «решку», вторая на «орла».
Из них благоприятными будут
два исхода.

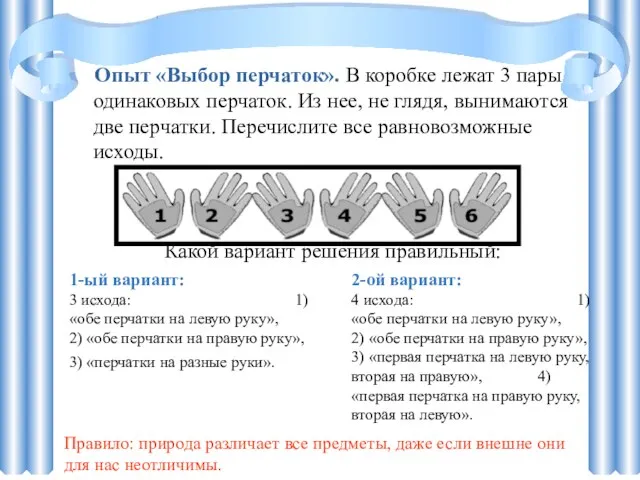
Опыт «Выбор перчаток». В коробке лежат 3 пары одинаковых перчаток. Из нее, не глядя, вынимаются две перчатки. Перечислите все равновозможные исходы.
Какой вариант решения правильный:
Правило: природа различает все предметы, даже если внешне они для нас неотличимы.
1-ый вариант: 3 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «перчатки на разные руки».
2-ой вариант: 4 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «первая перчатка на левую руку, вторая на правую», 4) «первая перчатка на правую руку, вторая на левую».

Вывод:
Формула классической вероятности дает очень простой способ вычисления вероятностей. Однако простота этой формулы обманчива. При ее использовании возникают два очень непростых вопроса:
Как выбрать систему исходов опыта так, чтобы они были равновозможными, и можно ли это сделать вообще?
Как найти числа т и п и убедиться в том, что они найдены верно?

Опыт человечества.
Вероятность попасть под дождь в Лондоне гораздо выше, чем в пустыне Сахара.
Весь наш жизненный опыт подсказывает, что любое событие считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким-то образом связана с частотой.

Частота случайного события.
Абсолютной частотой случайного события А в серии из N случайных опытов называется число NA , которое показывает, сколько раз в этой серии произошло событие А.

Частота случайного события.
Относительной частотой случайного события называют отношение числа появлений этого события к общему числу проведенных экспериментов:
где А – случайное событие по отношению к некоторому испытанию,
N раз проведено испытание и при этом событие А наступило в NA случаях.

Примеры
Пример 1. Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Какова частота рождения мальчика в такой серии наблюдений?
Ответ: 0,515

Примеры
Пример 2. За лето на Черноморском побережье было 67 солнечных дней. Какова частота солнечных дней на побережье за лето? Частота пасмурных дней?
Ответ: 0,728; 0,272.

Примеры
Пример 3. Отдел технического контроля обнаружил 5 бракованных изделий в партии из 1000 изделий. Найдите частоту изготовления бракованных изделий.
Ответ: 0,005

Примеры
Пример 4. Для выяснения качества семян было отобрано и высеяно в лабораторных условиях 1000 штук. 980 семян дали нормальные всходы. Найдите частоту нормального всхода семян.
Ответ: 0,98

Фундаментальным свойством относительных частот является тот факт, что с увеличением числа опытов относительная частота случайного события постепенно стабилизируется и приближается к вполне определенному числу, которое и следует считать его вероятностью.

Проверка
Пример 5. Подбрасывание монеты. А – выпадает герб.
Классическая вероятность: всего 2 исхода,
1 исход события А:

Проверка
Пример 5. Французский естествоиспытатель Бюффон (XVIII в.) бросил монету 4040 раз, и при этом герб выпал в 2048 случаях. Следовательно, частота выпадения герба в данной серии испытаний равна:
Жорж Бюффон

Проверка
Пример 5. Английский математик Карл Пирсон (1857-1936) бросал монету 24000 раз, причем герб выпал 12012 раз. Следовательно, частота выпадения герба в данной серии испытаний равна:
Карл Пирсон

Результаты
Вывод
Пример 5 подтверждает естественное предположение о том, что вероятность выпадения герба при одном бросании монеты равна 0,5.

Статистическая вероятность
Вероятность случайного события приближенно равна частоте этого события, полученной при проведении большого числа случайных экспериментов: , где - число испытаний, в которых наступило событие А, N – общее число испытаний.

Задача №1.
Чтобы определить, как часто встречаются в лесопарке деревья разных пород, ребята провели следующие эксперименты. Каждый выбрал свою тропинку и по пути следования записывал породу каждого десятого дерева.
Результаты были занесены в таблицу:
Породы Сосна Дуб Береза Ель Осина Всего
Число деревьев 315 217 123 67 35 757
Оцените вероятность того, что выбранное наугад в этом парке дерево будет:
а) сосной;
б) хвойным;
в) лиственным.
Указание. Ответ запишите в виде десятичной дроби с тремя знаками после запятой.

Задача №1.
Решение:
а) A={выбранное наугад в парке дерево - сосна} NА = 315, N = 757, Р(А) = 315/757 ≈ 0,416;
б) В ={выбранное наугад в парке дерево - хвойное} NА = 315 + 67 = 382, N = 757.
Р(А) = 382/757 ≈ 0,505;
в) C = {выбранное наугад в парке дерево - лиственное} NА = 217 + 123 + 35 = 375, N = 757.
Р(А) = 375/757 ≈ 0,495.

По статистике, на каждые 1000 лампочек приходится 3 бракованные. Какова вероятность купить исправную лампочку?
Решение:
3/1000 = 0,003
1 – 0,003 = 0,997
Задача №2.

Демографы утверждают, что вероятность рождения близнецов равна 0,012. в скольких случаях из 10 000 рождений можно ожидать появление близнецов?
Решение:
Ответ: в 120 случаях.
Задача №3.