ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ R, L, C И МЕТОДЫ РЕШЕНИЯ

В последовательной цепи общим для всех элементов является протекающий по ним ток. Поэтому именно с него начинаем построение векторной диаграммы последовательной электрической цепи.
На рис. 4.2 изображаем вектор тока, например, горизонтально, хотя его направление можно выбирать произвольно. Далее строятся векторы напряжений на всех элементах.
В соответствии со вторым законом Кирхгофа можно записать вектор входного напряжения:
Сложение векторов удобнее выполнять по правилу многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
Полученная диаграмма называется топографической векторной диаграммой.

Известно, что напряжение на активном сопротивлении R совпадает по фазе с током, поэтому вектор UR направлен по вектору тока I.
К концу вектора UR пристраиваем вектор UL и направляем его вверх под углом 90°, так как напряжение на индуктивности UL опережает ток на 90°.
Напряжение на ёмкости UC находится в противофазе с UL , т. е. отстаёт от тока на 90°, поэтому вектор UС , пристроенный к концу вектора UL, направлен вниз.
Сумма векторов UR + UL + UC даёт вектор напряжения U.

Величины напряжений на отдельных элементах цепи известны, согласно закону Ома:
По теореме Пифагора, из треугольника оab находим:
где Z – полное сопротивление цепи,
X – общее реактивное сопротивление,
Угол сдвига фаз между напряжением U и током I также определяется из треугольника oab:

Векторная диаграмма, изображенная на рис. 4.2, построена для случая, когда UL > UC .
Это имеет место при XL > XC, когда в цепи преобладает индуктивность и цепь носит активно-индуктивный характер. В этом случае общий ток I отстаёт по фазе от входного напряжения на угол ϕ.
Возможны также режимы, когда UL < UC и UL = UC .

Изобразим отдельно треугольник oab. Этот треугольник называется треугольником напряжений (рис. 4.3).
Рис. 4.3.
Проекция вектора напряжения U на вектор тока I называется активной составляющей напряжения, обозначается Ua, и равна падению напряжения на активном сопротивлении:
Треугольник
напряжений
Треугольник
сопротивлений
Реактивная составляющая напряжения Up – это проекция вектора напряжения на направление, перпендикулярное вектору тока, она равна падению напряжения на суммарном реактивном сопротивлении цепи:
Если все стороны треугольника напряжений разделить на ток, то получим треугольник сопротивлений, которому соответствуют формулы:

Режим, когда в цепи, содержащей последовательно соединенные активное сопротивление, индуктивность и ёмкость, ток совпадает по фазе с напряжением (рис. 4.4) называют резонансом напряжения. Это означает, что входное реактивное сопротивление в цепи равно нулю:
Резонанс напряжений
Рис. 4.4.
В этом случае
и цепь носит чисто активный характер, т.е.
,
и сдвиг фаз отсутствует
.

Так как при резонансе , то соответственно:
Напряжения на индуктивности и ёмкости в этом режиме равны по величине и, находясь в противофазе (сдвиг фаз 1800), компенсируют друг друга. Всё приложенное к цепи напряжение приходится на её активное сопротивление.
Напряжение на индуктивности и ёмкости может значительно превышать напряжение на входе цепи. Их отношение, называемое добротностью контура Q, определяется величинами индуктивного (или ёмкостного) и активного сопротивлений:
Добротность показывает, во сколько раз напряжения на индуктивности и ёмкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать несколько сотен единиц.

При резонансе
или
Решив это уравнение относительно f, получим:
где f0 – собственная частота колебаний контура. Таким образом, при резонансе напряжений частота f источника напряжения равна собственной частоте f0 колебаний контура.
При резонансе напряжения
Величину
называют волновым сопротивлением контура.
Тогда добротность Q равна

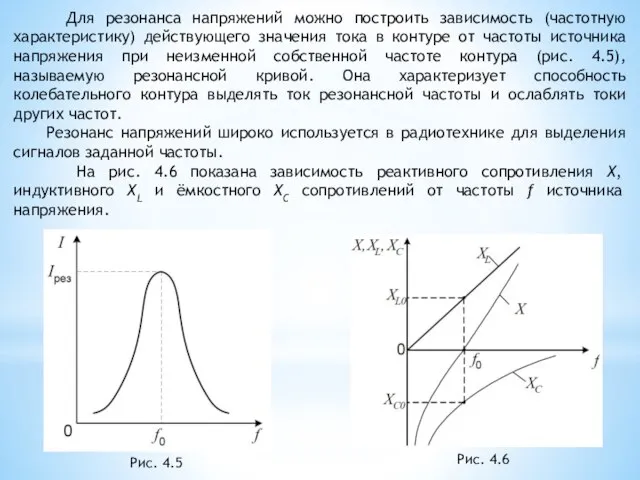
Для резонанса напряжений можно построить зависимость (частотную характеристику) действующего значения тока в контуре от частоты источника напряжения при неизменной собственной частоте контура (рис. 4.5), называемую резонансной кривой. Она характеризует способность колебательного контура выделять ток резонансной частоты и ослаблять токи других частот.
Резонанс напряжений широко используется в радиотехнике для выделения сигналов заданной частоты.
На рис. 4.6 показана зависимость реактивного сопротивления X, индуктивного XL и ёмкостного XC сопротивлений от частоты f источника напряжения.
Рис. 4.6
Рис. 4.5

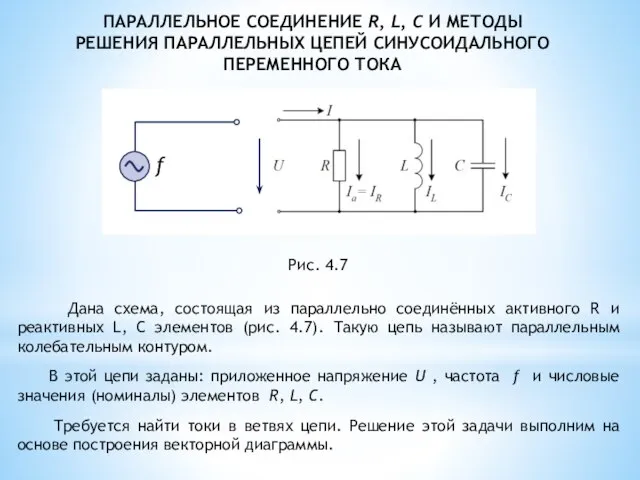
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ R, L, C И МЕТОДЫ
РЕШЕНИЯ ПАРАЛЛЕЛЬНЫХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО
ПЕРЕМЕННОГО ТОКА
f
Дана схема, состоящая из параллельно соединённых активного R и реактивных L, C элементов (рис. 4.7). Такую цепь называют параллельным колебательным контуром.
В этой цепи заданы: приложенное напряжение U , частота f и числовые значения (номиналы) элементов R, L, C.
Требуется найти токи в ветвях цепи. Решение этой задачи выполним на основе построения векторной диаграммы.
Рис. 4.7

Запишем токи ветвей:
Рис. 4.8
Для определения общего тока I необходимо построить векторную диаграмму (рис. 4.8).
Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей схемы.
Ток через резистор совпадает по фазе с приложенным напряжением, ток через индуктивность IL отстает по фазе от напряжения на 90°, ток через емкость IС находится в противофазе с IL.

Из векторной диаграммы имеем:
где Y – полная проводимость цепи
B – общая реактивная проводимость

Треугольник
токов
Треугольник
проводимостей
Рис. 4.9.
Векторы токов на диаграмме образуют треугольник токов (рис. 4.9). При этом вектор Ia – активная составляющая тока, Ia =UG; Ip – реактивная составляющая тока, которая определяется как разность длин векторов:
Разделив все стороны треугольника токов на U , получим треугольник проводимостей (рис. 4.9). Стороны треугольника проводимостей связаны следующими соотношениями:
Векторные диаграммы на рис. 4.8, 4.9 построены для случая, когда IL > IC . Это имеет место при ВL > ВC , когда в цепи преобладает индуктивность, и цепь носит активно-индуктивный характер.
В этом случае общий ток I отстаёт по фазе от входного напряжения на угол ϕ. Возможны также режимы, когда IL < IC и IL = IC .

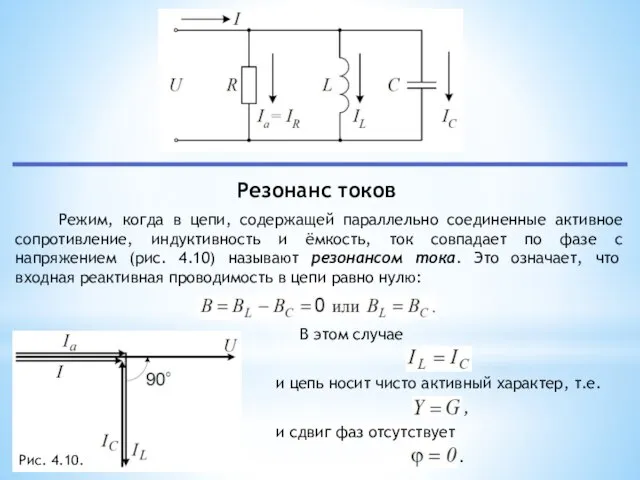
Режим, когда в цепи, содержащей параллельно соединенные активное сопротивление, индуктивность и ёмкость, ток совпадает по фазе с напряжением (рис. 4.10) называют резонансом тока. Это означает, что входная реактивная проводимость в цепи равно нулю:
Резонанс токов
Рис. 4.10.
В этом случае
и цепь носит чисто активный характер, т.е.
,
и сдвиг фаз отсутствует
.

Для того чтобы ток I в неразветвленной части цепи совпадал по фазе с напряжением источника, реактивный ток индуктивной ветви IL должен быть равен реактивному току ёмкостной ветви IC , т.е. IL = IC . В этом случае эти токи, находясь в противофазе, компенсируют друг друга. В итоге весь ток, подходящий к разветвленной цепи, носит активный характер.
Полная проводимость цепи при резонансе токов равна:
Так как при резонансе токов BL = BC, то соответственно
При этом условии частота f , при которой наступает резонанс токов, совпадает с собственной частотой f0 контура: