Слайд 2Виды карт
Карта дискретна. Нужно найти путь на графе
Карта непрерывна. Нужно найти векторную

функцию
Комбинация двух подходов: об этом позже
Слайд 3Поиск пути на графе
Найти путь значит найти последовательность рёбер, от исходной вершины

к искомой
Классические алгоритмы: Дейкстры, Флойда,
Волновой алгоритм
А* - наиболее распространённый в играх
Слайд 4А* Общие сведения
Впервые упомянут в 1968 году Питером Хартом Нильсом Нильсоном и

Бертраном Рафаэлем.
Является эвристическим
Всегда находит решение, если оно существует
По сути является обобщённым алгоритмом Дейкстры
Лёгок в реализации
Слайд 5А* Описание алгоритма
Алгоритм А* оперирует с двумя списками: открытым и закрытым. В

открытый список помещаются клетки, которые нужно проверить. В закрытые те, что уже не нужно проверять
То, какую клетку проверить первой определяется по значению F=G+H. G – Стоимость передвижения из стартовой клетки в исходную с учётом данной H – эвристическая функция
Слайд 6А* описание алгоритма
1) Добавляем стартовую клетку в открытый список.
2) Повторяем следующее:
a) Ищем

в открытом списке клетку с наименьшей стоимостью F. Делаем ее текущей клеткой.
b) Помещаем ее в закрытый список. (И удаляем с открытого)
c) Для каждой из соседних 8-ми клеток …
Если клетка непроходимая или она находится в закрытом списке, игнорируем ее. В противном случае делаем следующее.
Если клетка еще не в открытом списке, то добавляем ее туда. Делаем текущую клетку родительской для это клетки. Расчитываем стоимости F, G и H клетки.
Если клетка уже в открытом списке, то проверяем, не дешевле ли будет путь через эту клетку. Для сравнения используем стоимость G. Более низкая стоимость G указывает на то, что путь будет дешевле. Эсли это так, то меняем родителя клетки на текущую клетку и пересчитываем для нее стоимости G и F. Если вы сортируете открытый список по стоимости F, то вам надо отсортировать свесь список в соответствии с изменениями.
d) Останавливаемся если:
Добавили целевую клетку в открытый список, в этом случае путь найден.
Или открытый список пуст и мы не дошли до целевой клетки. В этом случае путь отсутствует.
3) Сохраняем путь. Двигаясь назад от целевой точки, проходя от каждой точки к ее родителю до тех пор, пока не дойдем до стартовой точки. Это и будет наш путь
Слайд 7Проблемы А*
Сглаживание пути
Рост потребляемой памяти
Одновременный поиск

Слайд 8Проблемы А*: сглаживание пути
Неестественная траектория
Зигзагообразная траектория
Путь по центрам клеток

Слайд 9Проблемы А*: память и скорость
Улучшаем алгоритм
Улучшаем эвристику
Укрупняем клетки(двупроходный алгоритм)
Комбинируем с

другими алгоритмами
Слайд 10Метод потенциальных полей
Препятствия отталкивают, цель притягивает
Основная проблема – локальные минимумы
Локальные минимумы обходим

итерациями
Не подходит для больших расстояний
Быстрый
Слайд 11Метод виртуальных отталкивающих клеток
Вариант предидущего метода
Препятствия режутся на клетки
Отталкивают клетки, которые близко
Более
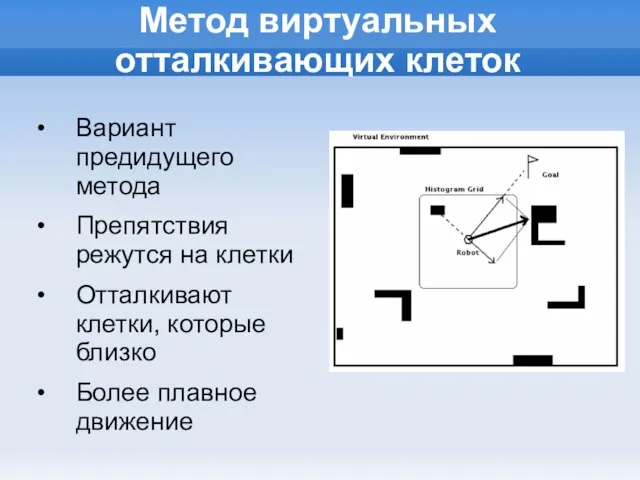
плавное движение
Слайд 12Комбинируем методы поиска
Делим мир на локации
От локации к локации – А*
Внутри локации

метод потенциальных полей
Локации это выпуклые фигуры или фигуры содержащие точку видимости
Точка видимости, это точка из которой можно провести отрезок в любую точку локации целиком находящийся в ней












 Взаимодействие банков и страховых компаний: новые тренды развития рынка
Взаимодействие банков и страховых компаний: новые тренды развития рынка ЭЛЕКТРИЧЕСКОЕ ОТОПЛЕНИЕ: КОНВЕКТОРЫ ENSTO
ЭЛЕКТРИЧЕСКОЕ ОТОПЛЕНИЕ: КОНВЕКТОРЫ ENSTO Возникновение искусства и религии
Возникновение искусства и религии Сроки проведения вступительных испытаний в гимназию в 2012 году
Сроки проведения вступительных испытаний в гимназию в 2012 году Число и цифра 5
Число и цифра 5 Travel America
Travel America Тема ВОВ в литературе
Тема ВОВ в литературе Материаловедение в графическом дизайне
Материаловедение в графическом дизайне В музее народной игрушки
В музее народной игрушки Квест-игра. Путешествие по городу Скульптура
Квест-игра. Путешествие по городу Скульптура Naumen Network Manager
Naumen Network Manager Международное сообщество фотоники и оптоинфоматики. SPIE Student Chapter PSUTI
Международное сообщество фотоники и оптоинфоматики. SPIE Student Chapter PSUTI Хронический гепатит В и С.Новые перспективы лечения с использованием препарата Ингарон
Хронический гепатит В и С.Новые перспективы лечения с использованием препарата Ингарон Русская деревянная архитектура Храмостроительс тво
Русская деревянная архитектура Храмостроительс тво  Классификация фитнес-программ и их специфические особенности
Классификация фитнес-программ и их специфические особенности Российская империя на рубеже 18-19 вв.
Российская империя на рубеже 18-19 вв. БД_л6_Join
БД_л6_Join The Present Indefinite Tense
The Present Indefinite Tense Употребление однородных членов с обобщающими словами
Употребление однородных членов с обобщающими словами Изделия народных мастеров
Изделия народных мастеров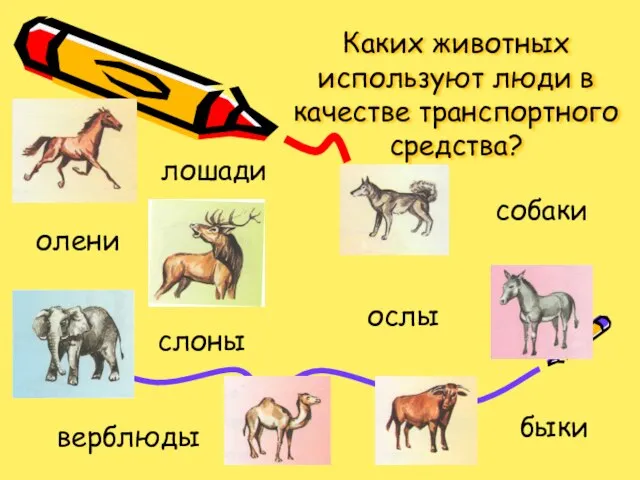 Каких животных используют люди в качестве транспортного средства?
Каких животных используют люди в качестве транспортного средства? Тета хилинг в Витебске. Новая технология исцеления
Тета хилинг в Витебске. Новая технология исцеления Общегосударственный классификатор РБ
Общегосударственный классификатор РБ Случаи вычитания 16 -
Случаи вычитания 16 - The Earth is in danger
The Earth is in danger  Путешествие в мир правового общества
Путешествие в мир правового общества Инструкиция по работе в АСУ РСО (дополнительное образование)
Инструкиция по работе в АСУ РСО (дополнительное образование) Настоящие и будущие проблемы развития российской автомобильной промышленности
Настоящие и будущие проблемы развития российской автомобильной промышленности