Архимед

Наше математическое состязание посвящено 300-летию со дня рождения
Михаила Васильевича Ломоносова

Желаем
удачи!

1
тур

1 ТУР ЗАДАЧА 1 УСЛОВИЕ:
Расставьте знаки арифметических действий и скобки там, где считаете нужным, чтобы получилось верное равенство:
2 4 6=3 3 3

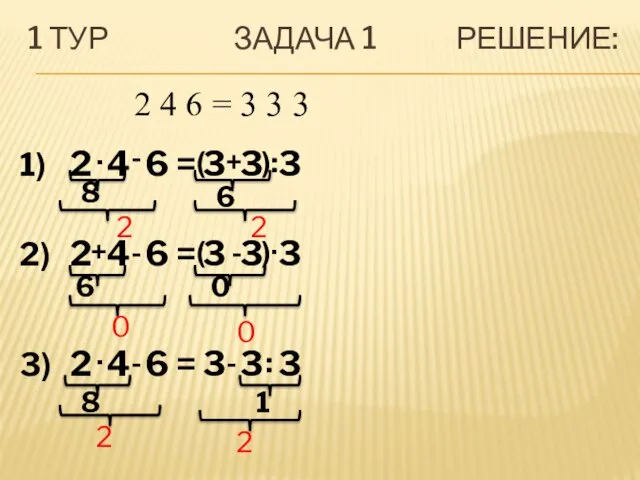
1 ТУР ЗАДАЧА 1 РЕШЕНИЕ:
2 4 6 = 3 3 3 1) 2 4 6 = 3 3 3
2) 2 4 6 = 3 3 3
3) 2 4 6 = 3 3 3
·
-
(
)
-
+
:
+
(
)
-
·
·
-
-
:
2
8
2
2
6
0
0
6
2
8
0
1

1 ТУР ЗАДАЧА 2 УСЛОВИЕ:
Нужно разместить 17 кроликов так, чтобы в каждой клетке было разное количество кроликов. Какое наибольшее число клеток понадобится?

1 ТУР РЕШЕНИЕ: ЗАДАЧА 2
Для того, чтобы использовать наибольшее количество клеток, с неповторяющимся количеством кроликов в них, нужно рассаживать в одну клетку минимальное количество кроликов.
Таким образом, в первую клетку – одного кролика, во вторую – 2, в третью – 3, в четвертую – 4.
Остается 7 кроликов, но это число мы не можем представить в виде суммы 2-х и более чисел, которые не будут повторяться с тем числом кроликов, находящихся с 1-ой по 4-ую клетки.
Следовательно, мы вынуждены поместить всех оставшихся кроликов в одну клетку. Таким образом получается, что максимальное число клеток равно 5.
I
II
III
IV
1
2
3
4
Ответ: 5 клеток

1 ТУР ЗАДАЧА 3 УСЛОВИЕ:
Найти сумму всех трёхзначных чисел, произведение цифр которых равно 3.

1 ТУР ЗАДАЧА 3 РЕШЕНИЕ:
Произведение трех цифр может быть равно 3 только, если это цифры 1,1, и 3.
Рассмотрим все возможные трехзначные числа, которые можно составить из этих цифр.
Это числа:
113
131
311
Их сумма равна 555.

результаты
1
тур

1
тур
апелляция

2
тур

2 ТУР ЗАДАЧА 1 УСЛОВИЕ:
На выставку привезли 25 собак.
5 из них средние, 8-маленькие, остальные большие.
Только 10 из участников выставки породистые, остальные-дворняжки.
Среди дворняжек поровну больших, маленьких и средних.
Сколько больших породистых собак привезли на выставку?

2 ТУР ЗАДАЧА 1 РЕШЕНИЕ:
5 + 8 + X = 25
13+ X = 25
X = 12
12
10 + Y = 25
Y = 15
X
Y
3 · Z = 15
Z = 5
Z
Z
Z
15
5
5
5
5 + M = 12
M = 7
Ответ: 7 собак
На выставку привезли 25 собак.
5 из них средние, 8-маленькие, остальные большие.
Только 10 из участников выставки породистые, остальные-дворняжки.
Среди дворняжек поровну больших, маленьких и средних.

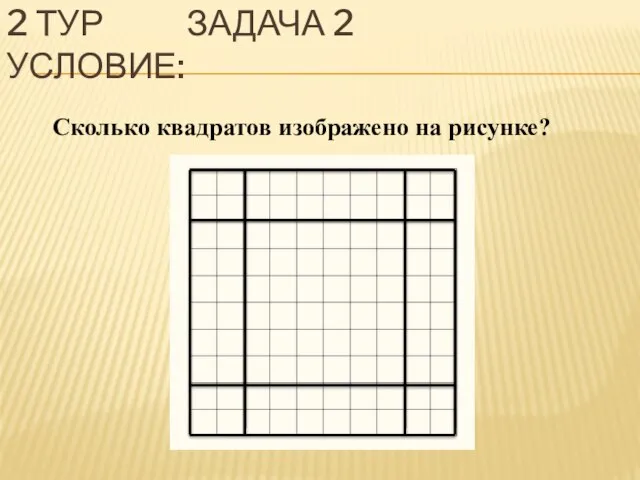
2 ТУР ЗАДАЧА 2 УСЛОВИЕ:
Сколько квадратов изображено на рисунке?

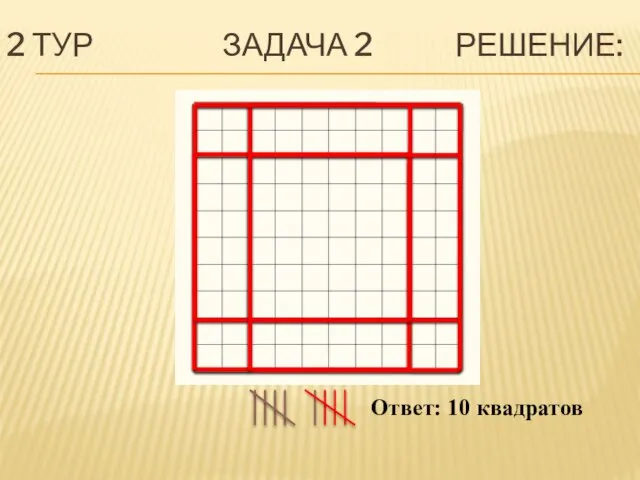
2 ТУР ЗАДАЧА 2 РЕШЕНИЕ:
Ответ: 10 квадратов

2 ТУР ЗАДАЧА 3 УСЛОВИЕ:
Будет ли сумма чисел
1 + 2 + 3 + … + 2005 + 2006 + 2007 делиться на 2007? Ответ обоснуйте.

2 ТУР ЗАДАЧА 3 РЕШЕНИЕ:
1 + 2 + 3 + … + 2005 + 2006 + 2007
= (1 + 2006) + (2 + 2005) + … + 2007
=
=
= 2007 + 2007 + 2007 + ... + 2007.
2007
2007
2007
2007
Ответ: да, будет
2007

2
тур
результаты

2
тур
апелляция

3
тур

3 ТУР ЗАДАЧА 1 УСЛОВИЕ:
В забеге участвовали 11 спортсменов. Число спортсменов, прибежавших раньше Васи в 4 раза меньше, числа тех, кто прибежал позже него. Какое место занял Вася?

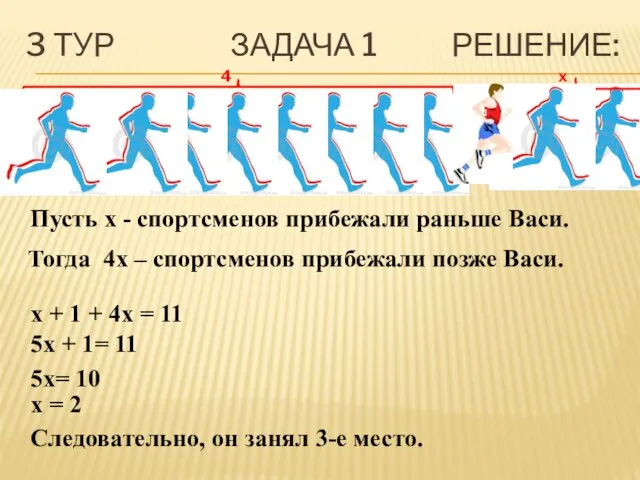
3 ТУР ЗАДАЧА 1 РЕШЕНИЕ:
Пусть x - спортсменов прибежали раньше Васи.
x + 1 + 4x = 11
5x + 1= 11
5x= 10
x = 2
Следовательно, он занял 3-е место.
4x
x
Тогда 4x – спортсменов прибежали позже Васи.

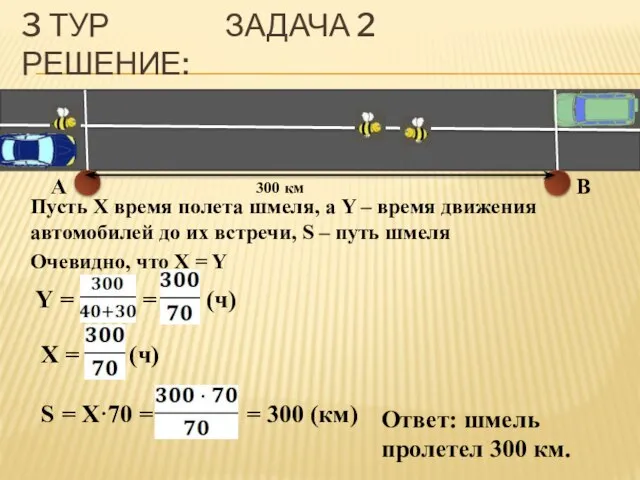
3 ТУР ЗАДАЧА 2 УСЛОВИЕ:
Из города A и B, расстояние между которыми 300 км, выехали 2 машины навстречу друг другу со скоростями 40 км/ч и 30 км/ч соответственно.
Из города A одновременно с машиной вылетел шмель, со скоростью 70 км/ч, направляющийся, к городу B.
Повстречав автомобиль, выехавший из пункта B, он сразу полетел к A. Повстречав автомобиль, выехавшей из пункта A, он сразу полетел к B, и так летал, до тех пор, пока машины не встретились.
Какой путь пролетел шмель?
A
B
300 км

3 ТУР ЗАДАЧА 2 РЕШЕНИЕ:
A
B
300 км
Пусть X время полета шмеля, а Y – время движения автомобилей до их встречи, S – путь шмеля
Очевидно, что X = Y
Y = = (ч)
X = (ч)
S = X·70 = = 300 (км)
Ответ: шмель пролетел 300 км.

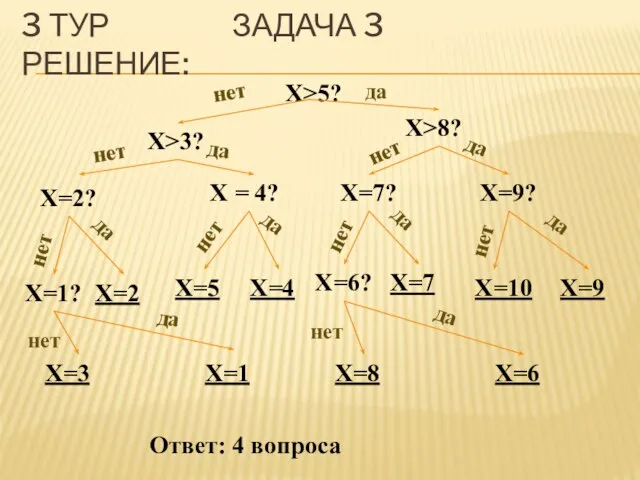
3 ТУР ЗАДАЧА 3 УСЛОВИЕ:
Первый игрок загадывает число от 1 до 10. Второй игрок задает первому вопросы, на которые он отвечает либо «да», либо «нет». Какое минимальное количество вопросов нужно задать второму игроку первому, чтобы точно определить какое это число?

3 ТУР ЗАДАЧА 3 РЕШЕНИЕ:
X>5?
X>3?
X>8?
X=2?
нет
нет
да
да
X = 4?
X=1?
X=2
X=5
X=4
X=7?
X=9?
X=9
X=10
X=6?
X=7
X=3
X=1
X=8
X=6
нет
нет
нет
нет
нет
нет
нет
да
да
да
да
да
да
да
Ответ: 4 вопроса

3
тур
результаты

3
тур
апелляция

4
тур

4 ТУР ЗАДАЧА 1 УСЛОВИЕ:
В банку попал 1 микроб, и через 35 минут банка была наполнена микробами, причем известно, что количество микробов ежеминутно удваивалось. За сколько минут банка будет наполнена микробами наполовину?

4 ТУР ЗАДАЧА 1 РЕШЕНИЕ:
Ответ: банка будет наполнена микробами наполовину за 34 минуты.

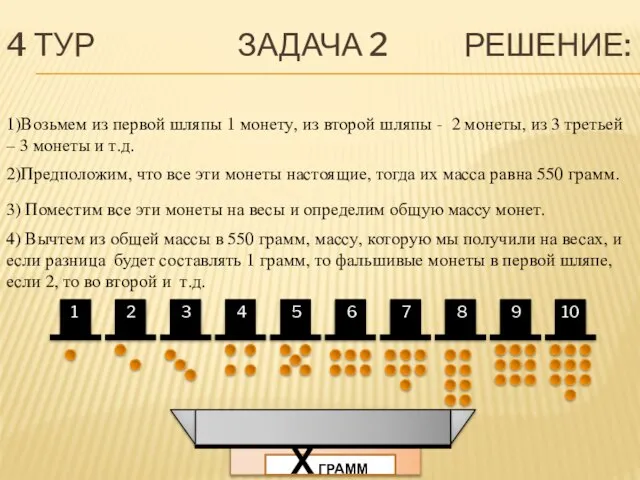
4 ТУР ЗАДАЧА 2 УСЛОВИЕ:
На столе лежат десять пронумерованных шляп. В каждой шляпе лежит по десять золотых монет. В девяти шляпах настоящие и только в одной поддельные. Настоящая весит 10 грамм, а поддельная - 9. В помощь даны электронные весы, которые измеряют с точностью до грамма. Как за одно взвешивание определить в какой шляпе находятся фальшивые монеты?

1)Возьмем из первой шляпы 1 монету, из второй шляпы - 2 монеты, из 3 третьей – 3 монеты и т.д.
1
3
2
4
5
6
7
8
9
10
X ГРАММ
2)Предположим, что все эти монеты настоящие, тогда их масса равна 550 грамм.
3) Поместим все эти монеты на весы и определим общую массу монет.
4) Вычтем из общей массы в 550 грамм, массу, которую мы получили на весах, и если разница будет составлять 1 грамм, то фальшивые монеты в первой шляпе, если 2, то во второй и т.д.
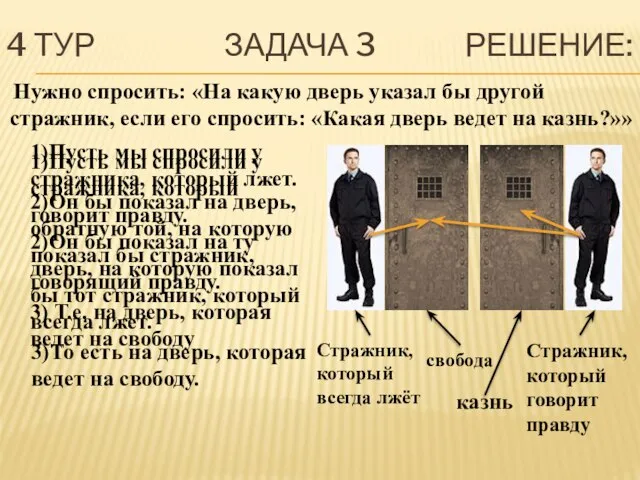
4 ТУР ЗАДАЧА 2 РЕШЕНИЕ:

4 ТУР ЗАДАЧА 3 УСЛОВИЕ:
Человек попал в тюрьму. В день казни ему был дан последний шанс: он стоит в коридоре с двумя дверьми, перед каждой дверью стоит стражник, одна дверь ведет на свободу, другая- на казнь. Также известно, что один из стражников всегда говорит правду, а другой всегда лжёт.
Какой вопрос должен задать человек стражнику, чтобы точно избежать казни?

4 ТУР ЗАДАЧА 3 РЕШЕНИЕ:
Нужно спросить: «На какую дверь указал бы другой стражник, если его спросить: «Какая дверь ведет на казнь?»»
1)Пусть мы спросили у стражника, который говорит правду.
Стражник, который всегда лжёт
Стражник, который говорит правду
свобода
казнь
2)Он бы показал на ту дверь, на которую показал бы тот стражник, который всегда лжет.
3)То есть на дверь, которая ведет на свободу.
1)Пусть мы спросили у стражника, который лжет.
2)Он бы показал на дверь, обратную той, на которую показал бы стражник, говорящий правду.
3) Т.е. на дверь, которая ведет на свободу

4
тур
результаты

4
тур
апелляция