Слайд 2Модель PRAM
Модель PRAM: Parallel Random-Access Memory
Позволяет учитывать ограничения, связанные с одновременным доступом

к памяти
Является идеализированной моделью архитектуры SMP (Symmetric MultiProcessor, Shared Memory Processor)
Слайд 3Модель PRAM
Процессоры П0, П1, …, Пp–1 используют общую память, состоящую из множества
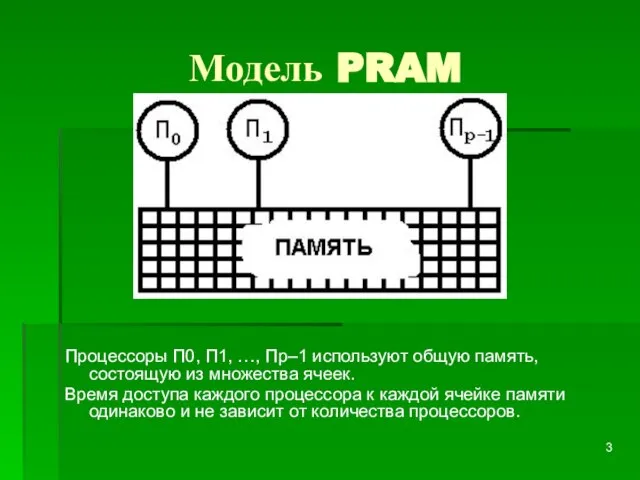
ячеек.
Время доступа каждого процессора к каждой ячейке памяти одинаково и не зависит от количества процессоров.
Слайд 4Модель PRAM
Один шаг (такт) работы PRAM-машины синхронизирован по фазам:
Чтение данных из памяти.
Обработка

данных.
Запись результата в память.
Слайд 5Режимы чтения и записи
Режимы чтения данных из памяти:
Одновременное (Concurrent Read)
Исключающее (Exclusive Read)
Режимы

записи в память:
Одновременная (Concurrent Write)
Исключающая (Exclusive Write)
Слайд 6Варианты одновременной записи
Одновременная запись одинакового значения
Произвольная запись: сохраняется произвольное значение из множества

записываемых
Запись в зависимости от приоритетов процессоров
Комбинация записываемых значений
Слайд 7Виды PRAM машин и алгоритмов

Слайд 8ЗАДАЧА НАХОЖДЕНИЯ КОРНЕЙ ДВОИЧНОГО ЛЕСА
Пример CREW-алгоритма

Слайд 9Пример CREW-алгоритма
Дано: Лес, состоящий из бинарных деревьев. Деревья заданы следующим образом: для

каждой вершины имеется указатель на её родителя. Для корней деревьев этот указатель пуст.
Требуется: для каждой вершины найти корень дерева, которому она принадлежит
Слайд 10Пример CREW-алгоритма
Представление входных данных:
вершины пронумерованы,
ребра деревьев заданы с помощью массива parent:

элемент parent[i] представляет номер вершины, являющейся родителем для вершины с номером i.
Слайд 11Пример CREW-алгоритма
Результат работы алгоритма — массив root. В ячейке root[i] хранится вершины,
![Пример CREW-алгоритма Результат работы алгоритма — массив root. В ячейке root[i] хранится](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/383097/slide-10.jpg)
являющейся корнем дерева, в которое входит вершина i.
Массивы parent и root хранятся в общей памяти.
Слайд 12CREW-алгоритм
Для каждого процессора Pi выполнить
Если parent[i] = NIL, то root[i] :=
![CREW-алгоритм Для каждого процессора Pi выполнить Если parent[i] = NIL, то root[i]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/383097/slide-11.jpg)
i;
Пока существует узел i, для которого parent[i] ≠ NIL, выполнять:
Для каждого процессора i выполнить
Если parent[i] ≠ NIL, то
{
root[i] := root[parent[i]];
parent[i] := parent[parent[i]];
}
Слайд 13Анализ CREW-алгоритма
Временная сложность алгоритма:
O(log2 d),
где d — наибольшая глубина дерева

в заданном лесе.
Можно показать, что ни один EREW-алгоритм не может решить эту задачу за время, меньшее O(log2 n), где n — количество вершин в лесе
Слайд 14НАХОЖДЕНИЕ МАКСИМАЛЬНОГО ЭЛЕМЕНТА В МАССИВЕ
Пример CRCW-алгоритма

Слайд 15Пример CRCW-алгоритма
Дано: Массив n элементов
Требуется: Найти максимальный элемент

Слайд 16Пример CRCW-алгоритма
Способ решения
Количество процессоров: n2.
Каждый процессор нумеруется парой индексов.
Процессор с номером

(i,j) сравнивает A[i] и A[j].
Используется вспомогательный булевский массив m[i]. После выполнения сравнений m[i]=true ⇔ A[i] — наибольший элемент массива.
Результат помещается в переменную max.
Слайд 17CRCW-алгоритм
Для всех i от 0 до n–1 выполнить:
m[i] := true;
Для всех
![CRCW-алгоритм Для всех i от 0 до n–1 выполнить: m[i] := true;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/383097/slide-16.jpg)
i от 0 до n–1 и для всех j от 0 до n–1 выполнить:
Если A[i] < A[j], то m[i] := false;
Для всех i от 0 до n–1 выполнить:
Если m[i] = true, то max := A[i];
Вернуть max.
Слайд 18Анализ CRCW-алгоритма
Без использования параллельного чтения невозможно решить эту же задачу быстрее, чем

за время O(log n).
Представленный CRCW-алгоритм работает за время O(1) и требует n2 процессоров. Наилучший последовательный алгоритм работает за время O(n). Поэтому эффективность составляет 1/n, т.е. алгоритм не является эффективным по затратам.









![Пример CREW-алгоритма Результат работы алгоритма — массив root. В ячейке root[i] хранится](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/383097/slide-10.jpg)
![CREW-алгоритм Для каждого процессора Pi выполнить Если parent[i] = NIL, то root[i]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/383097/slide-11.jpg)




![CRCW-алгоритм Для всех i от 0 до n–1 выполнить: m[i] := true;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/383097/slide-16.jpg)

 Программы учебных дисциплин в компетентностном формате
Программы учебных дисциплин в компетентностном формате Скрипт (письмо потенциальному заказчику)
Скрипт (письмо потенциальному заказчику) Беседа о художнике Пластове и его картинах
Беседа о художнике Пластове и его картинах Измельчение мусора. Компания TiCon
Измельчение мусора. Компания TiCon Слоганы для рекламного агентства
Слоганы для рекламного агентства 12.09-16.09
12.09-16.09 Презентация на тему Технология обработки текстовой информации
Презентация на тему Технология обработки текстовой информации Родители ГИА-23
Родители ГИА-23 Рынок содержание и структура
Рынок содержание и структура  Абажур своими руками
Абажур своими руками Medbiolinе LLC
Medbiolinе LLC Юридические аспекты города-курорта Сочи как исторического поселения
Юридические аспекты города-курорта Сочи как исторического поселения Образование с Марусей
Образование с Марусей Фенс Сервис
Фенс Сервис Способы минимизации рисков инвесторов
Способы минимизации рисков инвесторов "ПАУТИНА - ЧУДО ПРИРОДЫ"
"ПАУТИНА - ЧУДО ПРИРОДЫ" Та женщина
Та женщина Цветные ресницы
Цветные ресницы Перфоративная язва
Перфоративная язва Русь с древнейших времен до конца XVI века
Русь с древнейших времен до конца XVI века Невербальная коммуникация
Невербальная коммуникация Виктимология. Синдромы
Виктимология. Синдромы Маршруты лыжных прогулок
Маршруты лыжных прогулок Современные направления развития образования
Современные направления развития образования СОЗДАНИЕ МУЛЬТИМЕДИЙНЫХ ПРЕЗЕНТАЦИЙ
СОЗДАНИЕ МУЛЬТИМЕДИЙНЫХ ПРЕЗЕНТАЦИЙ Презентация на тему Опасные ситуации криминального характера.
Презентация на тему Опасные ситуации криминального характера.  Предотказное состояние аппаратуры железнодорожной автоматики и телемеханики
Предотказное состояние аппаратуры железнодорожной автоматики и телемеханики Современная медиа-среда в России
Современная медиа-среда в России