Построение сечений в тетраэдре и параллелепипеде

Цель:
Научиться строить сечения
с помощью теоретических
знаний и практических навыков.

План построения сечения тетраэдра :
1.Если секущая плоскость и грань имеют общие точки, то сторону
сечения строим сразу, как отрезок, проходящий через две эти точки.
2.Если секущая и грань имеют одну общую точку и секущая плоскость
параллельна, то строим сторону сечения параллельно грани.
3.Если только одна общая точка, то ищем дополнительную точку:
Точку пересечения ребра этой грани со стороной сечения, лежащей в одной плоскости. Дальше проводим прямую, проходящую через общую точку и дополнительную. Затем обозначаем точку пересечения ребра этой грани и этой прямой и обводим сторону сечения.

План построения сечения параллелепипеда:
Если секущая плоскость и грань имеют две общие точки, то строим сторону сечения сразу как отрезок, проходящий через две эти точки.
2. Если секущая плоскость и грань имеют одну общую точку, и секущая плоскость параллельна, то строим сторону сечения параллельно ребру грани.
3. Если только одна общая точка, то ищем дополнительную точку – точку пересечения ребра этой грани со стороной сечения, лежащей в одной плоскости. Дальше проводим прямую, проходящую через общую точку и дополнительную точку. Затем обозначаем точку пересечения ребра этой грани и этой прямой и обводим сторону сечения.
4. Если грань имеет с сечением одну общую точку, то смотрим, в параллельной ей грани есть сторона сечения или нет; если да, то строим сторону сечения параллельно той стороне сечения; если нет, то строим дополнительную точку. Дополнительная точка – точка пересечения ребра грани и стороны сечения, лежащей в одной другой грани. Проводим прямую, проходящую через дополнительную и общую точку. Обводим сторону сечения.

Выполнения заданий:
Построить сечение тетраэдра АВСD, плоскостью, проходящей через точки Е, К, Р, если Е лежит на ребре AD, К лежит на ребре BD, Р лежит на ребре DC.

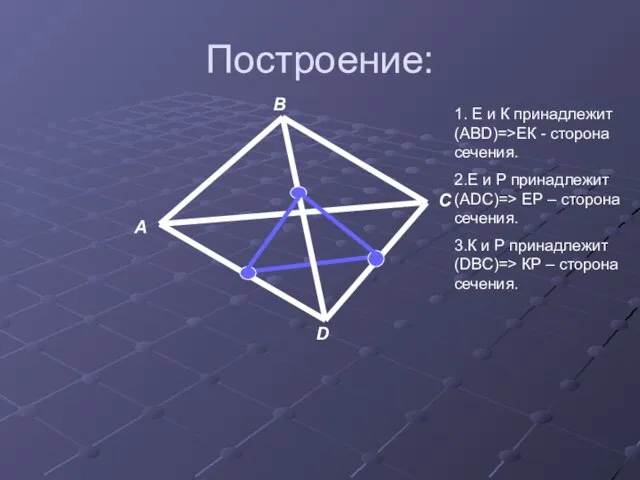
Построение:
А
В
С
D
1. Е и К принадлежит (АВD)=>ЕК - сторона сечения.
2.Е и Р принадлежит (АDC)=> ЕР – сторона сечения.
3.К и Р принадлежит (DBC)=> КР – сторона сечения.

Задача 2.
Построить сечение тетраэдра АВСD плоскостью, проходящей через точку К, лежащей на ребре АС и параллельно грани BDC.

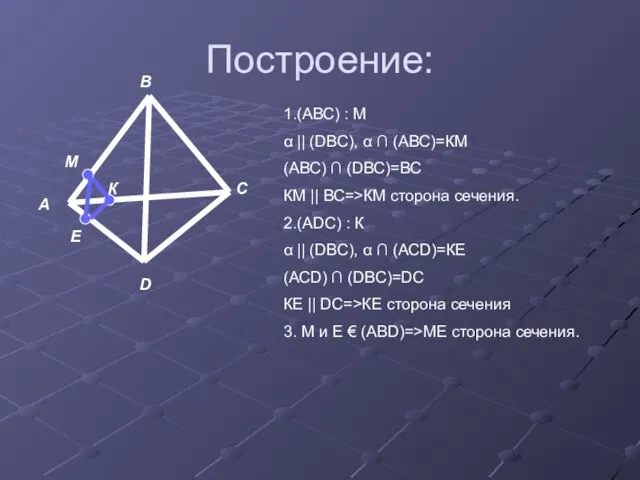
Построение:
А
В
С
D
К
Е
М
1.(АВС) : М
α || (DBC), α ∩ (АВС)=КМ
(АВС) ∩ (DВС)=ВС
КМ || ВС=>КМ сторона сечения.
2.(АDC) : К
α || (DBC), α ∩ (АСD)=КЕ
(АСD) ∩ (DВС)=DС
КЕ || DC=>КЕ сторона сечения
3. М и Е € (АВD)=>МЕ сторона сечения.

Задача 3.
Построить сечение тетраэдра АВСD плоскостью, проходящей через точки Е,М,Р, если Е лежит на ребре АD (ближе к D), P лежит на ребре АВ (ближе к А), М – середина ВС.

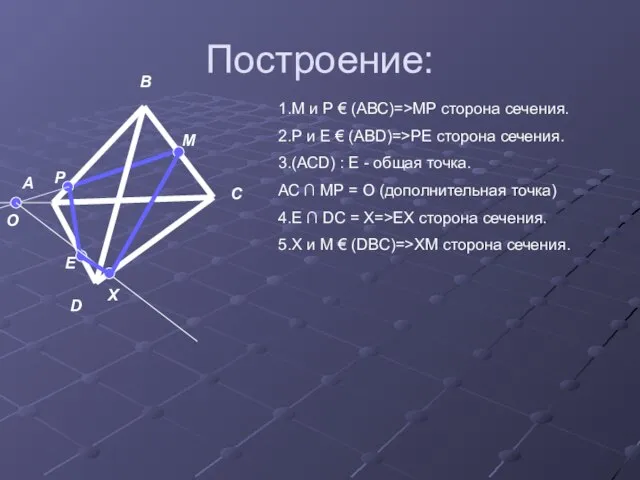
Построение:
А
В
С
D
Р
М
О
Х
Е
1.М и Р € (АВС)=>МР сторона сечения.
2.Р и Е € (АВD)=>РЕ сторона сечения.
3.(АСD) : Е - общая точка.
АС ∩ МР = О (дополнительная точка)
4.Е ∩ DC = Х=>ЕХ сторона сечения.
5.Х и М € (DBC)=>ХМ сторона сечения.

Задача 4.
Построить сечение параллелепипеда плоскостью, проходящей через точки М, К, F, если М лежит на АВ, к лежит на ВС, F лежит на ребре ВВ1.

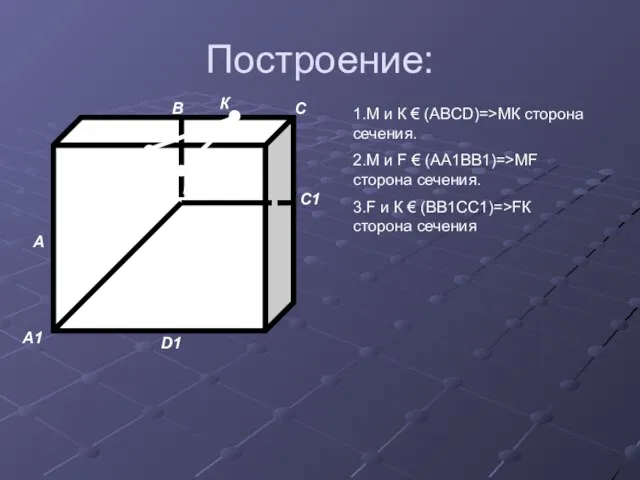
Построение:
А
В
С
D
D1
А1
В1
С1
М
К
F
1.М и К € (АВСD)=>МК сторона сечения.
2.М и F € (АА1ВВ1)=>МF сторона сечения.
3.F и К € (ВВ1СС1)=>FК сторона сечения

Задача 5.
Построить сечение параллелепипеда плоскостью, проходящей через точки Е, К, Р, если Е лежит на ребре А1В1 (ближе к А1), К – середина АD, Р лежит на ребре В1С1.

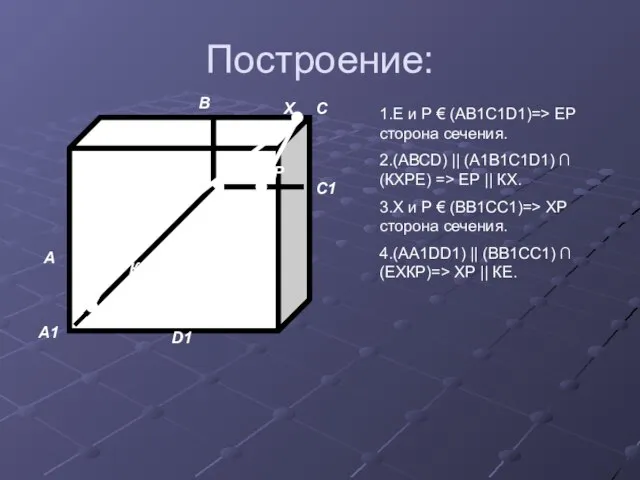
Построение:
А
D
А1
D1
В1
В
С
С1
Р
Е
К
Х
1.Е и Р € (АВ1С1D1)=> ЕР сторона сечения.
2.(АВСD) || (А1В1С1D1) ∩ (КХРЕ) => ЕР || КХ.
3.Х и Р € (ВВ1СС1)=> ХР сторона сечения.
4.(АА1DD1) || (ВВ1СС1) ∩ (ЕХКР)=> ХР || КЕ.

Задача 6.
Построить сечение параллелепипеда плоскостью, проходящей через точки М, К и параллельно ребру СС1, если М лежит на ребре А1В1, К лежит на ребре В1С1.

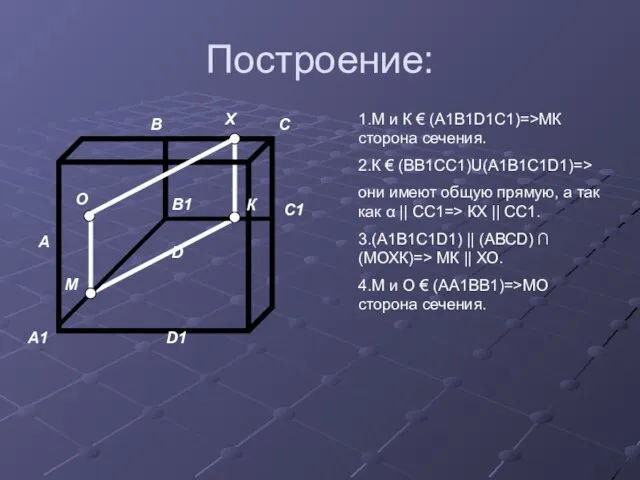
Построение:
А1
D1
D
А
В1
В
С1
С
К
Х
М
О
1.М и К € (А1В1D1С1)=>МК сторона сечения.
2.К € (ВВ1СС1)U(А1В1С1D1)=>
они имеют общую прямую, а так как α || СС1=> КХ || СС1.
3.(А1В1С1D1) || (АВСD) ∩ (МОХК)=> МК || ХО.
4.М и О € (АА1ВВ1)=>МО сторона сечения.

Задача 7.
Построить сечение параллелепипеда плоскостью, проходящей через точки Т, К, Р, если Т лежит на ребре АА1 (ближе к А1), К лежит на ребре В1С1 (ближе к С1), Р лежит на ребре В1А1 (ближе к В1).

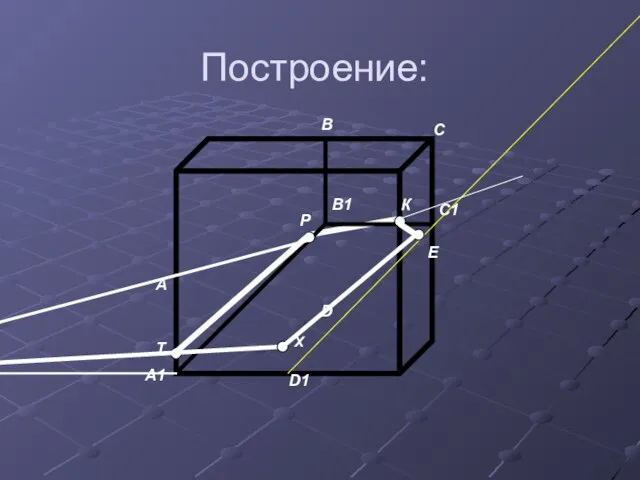
Построение:
А
D
А1
D1
В
С
С1
В1
Т
К
Р
Х
S
О
Е

Р и К € (А1В1С1D1)=>РК сторона с-я.
Т и Р € (АА1ВВ1)=> ТР сторона с-я.
А1D1 ∩ КР=S;ST ∩ DD1=Х
Т и Х € (АА1DD1)=>ТХ сторона с-я.
D1C1 ∩ ТР=О;ОХ ∩ D1С1=Е
Е и К € (А1В1С1D1)=>ЕК сторона с-я.
Х и Е € (DD1СС1)=>ХЕ сторона с-я.
ОБЪЯСНЕНИЕ: