Содержание
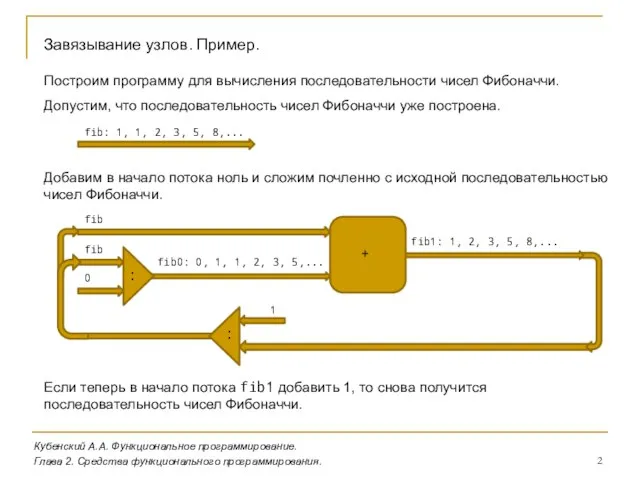
- 2. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Завязывание узлов. Пример. Построим программу для вычисления
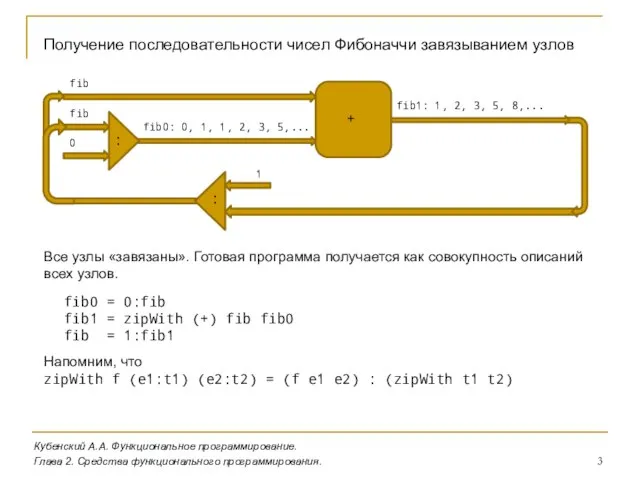
- 3. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Получение последовательности чисел Фибоначчи завязыванием узлов fib0
- 4. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Функциональное представление множеств: описание грамматики языка Рассматриваем
- 5. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Программирование регулярных выражений type Language = String
- 6. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Расширение техники работы с регулярными выражениями (
- 7. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Еще один пример функциональной программы 2 6
- 8. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Поиск по ассоциативному списку Пусть задан ассоциативный
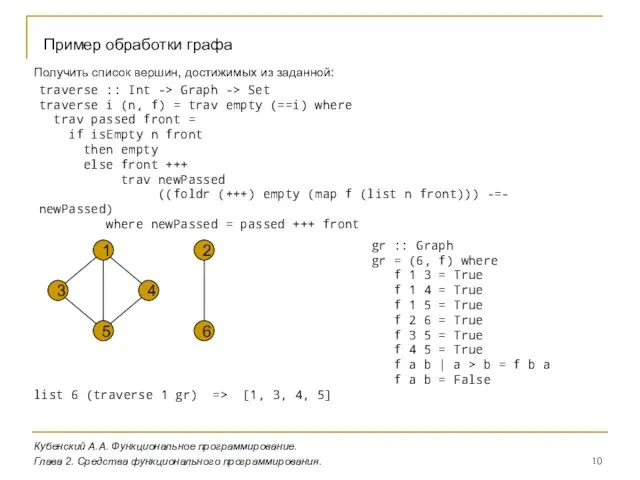
- 9. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Работа с функциональным представлением графа type Graph
- 10. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. 2 6 4 1 3 5 Пример
- 11. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. 2.4. Классы в Haskell. Класс определяет набор
- 12. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Пример: определение операций сравнения над деревьями data
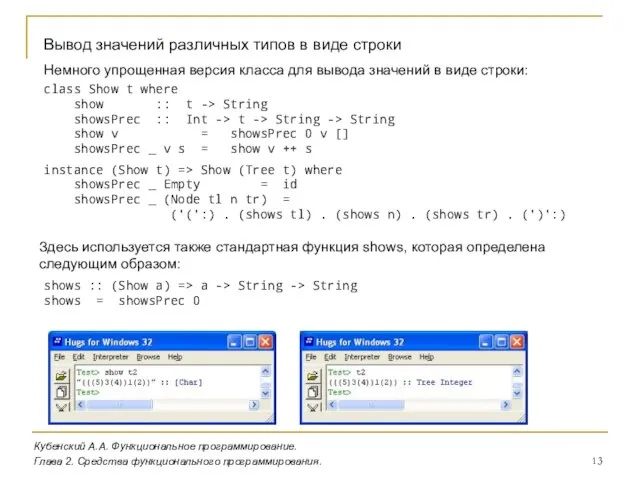
- 13. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Вывод значений различных типов в виде строки
- 14. Кубенский А.А. Функциональное программирование. Глава 2. Средства функционального программирования. Расширение классов class (Eq t) => Ord
- 16. Скачать презентацию









 Презентация на тему Православные праздники
Презентация на тему Православные праздники Chinese New Year Story PowerPoint
Chinese New Year Story PowerPoint Правовые основы организации школьного ученического самоуправления
Правовые основы организации школьного ученического самоуправления Почему грубит подросток
Почему грубит подросток Георгиевские кавалеры в СССР
Георгиевские кавалеры в СССР Отраслевой программный продукт для автоматизации операций по учёту товара в магазине при помощи ТСД
Отраслевой программный продукт для автоматизации операций по учёту товара в магазине при помощи ТСД Новые возможности FREE!ship Plus при проектировании судов и подводных аппаратов Доцент, к.т.н Тимошенко В.Ф., НУК, Николаев, Украина 21-23 ок
Новые возможности FREE!ship Plus при проектировании судов и подводных аппаратов Доцент, к.т.н Тимошенко В.Ф., НУК, Николаев, Украина 21-23 ок Лекция 1Экономическая и тарифная политика в энергетике
Лекция 1Экономическая и тарифная политика в энергетике ВКР: Реабилитация в уголовном судопроизводстве
ВКР: Реабилитация в уголовном судопроизводстве Особенности электроснабжения обогатительных фабрик. Категории качества электроэнергии. Лекция №1
Особенности электроснабжения обогатительных фабрик. Категории качества электроэнергии. Лекция №1 Чайная церемония в Японии
Чайная церемония в Японии Профиль наставника
Профиль наставника Сравнение с конкурентами
Сравнение с конкурентами Жизнь и творчество Д.Н.Ушакова
Жизнь и творчество Д.Н.Ушакова DiDi - такси
DiDi - такси Театр и музыка едины. Часть 3.1
Театр и музыка едины. Часть 3.1 Мониторинг качества образования с КМ-школой
Мониторинг качества образования с КМ-школой Школа родительского мастерства. Решение конфликтов
Школа родительского мастерства. Решение конфликтов Литература США XX века
Литература США XX века Лукойл запускает проект Старт в будущее
Лукойл запускает проект Старт в будущее Куклы из ниток
Куклы из ниток Презентация на тему ПОНЯТИЕ ИСТОЧНИКОВ КЛАССИФИКАЦИЙ И ВИДОВ ТРУДОВОГО ПРАВА
Презентация на тему ПОНЯТИЕ ИСТОЧНИКОВ КЛАССИФИКАЦИЙ И ВИДОВ ТРУДОВОГО ПРАВА Компьютерные тесты
Компьютерные тесты Зелёный пояс Славы
Зелёный пояс Славы Формирование информации об оценочных обязательствах, условиях обязательных и условных активах
Формирование информации об оценочных обязательствах, условиях обязательных и условных активах Искусство
Искусство 1. С помощью циркуля и линейки без шкалы делений нарисуйте треугольник по двум данным сторонам и углу между ними.
1. С помощью циркуля и линейки без шкалы делений нарисуйте треугольник по двум данным сторонам и углу между ними. Презентация на тему Биосферные резерваты
Презентация на тему Биосферные резерваты