Поверхностные состояния в сверхрешетке с шероховатой границей.

Введение
Граница твердого тела с вакуумом или другой средой может служить источником ряда особых энергетических состояний электронов – поверхностных состояний, т.е. состояний,пространственно локализованных у границы тела. Возможность существования у поверхности кристалла связанных состояний электронов впервые рассмотрел И.Е. Тамм [1].
В нашей работы мы рассматривали поверхностные состояния в полубесконечных сверхрешетках.
Сверхрешетками принято называть твердотельные структуры, в которых, помимо периодического потенциала кристаллической решетки, имеется дополнительный периодический потенциал, период которого существенно превышает постоянную решетки.
Параметры потенциала сверхрешеток можно варьировать в широких пределах, благодаря чему в сверхрешетках можно контролируемо изменять волновую функцию электронов, и зонную структуру спектра. Впервые такие системы были рассмотрены Л. В. Келдышем [2]. Сверхрешетки широко применяются в электронике и оптоэлектронике.
В общем случае поверхность не представляет собой резкого перехода от невозмущенного периодического потенциала к внешнему пространству. Следует также учитывать, что поверхность может быть покрыта неупорядоченным адсорбированным слоем. Такая шероховатость поверхности ведет к рассеянию поверхностной волны, представляющей поверхностные состояния электрона, на неровностях поверхности, в том числе поверхностная волна может преобразовываться в объемную волну. Представляет интерес оценить затухание поверхностного состояния, обусловленное таким рассеянием.

Постановка задачи
В простейшем однозонном приближении [3] для невырожденных энергетических зон кристаллической решетки уравнение Шредингера для огибающей функции имеет вид:
С целью максимально упростить задачу будем считать, что потенциалы ям имеют вид -функций. В рассматриваемой модели неровность поверхности можно описать, вводя зависимость мощности потенциала поверхностного слоя от координат точек слоя [4].
- период сверхрешетки
- мощность поверхностного потенциала
- потенциал внешнего пространства
- мощность потенциала сверхрешетки

В результате приходим к уравнению Шредингера:
- эффективная масса электрона
Z – ось в направлении препендикулярном плоскости сверхрешетки
- мощность потенциала поверхностного слоя
- мощность потенциала сверхрешетки
- мощность потенциала шероховатости поверхности
- потенциал внешнего пространства
Шероховатости поверхности будем считать случайными, т.е. есть случайная функция координат, среднее значение которой равно нулю. Будем также считать шероховатости статистически однородными с корреляционной функцией:
Решения уравнения для случая гладкой поверхности, т.е. , неоднократно обсуждались в литературе (см., например, [5]). В нашей модели при уравнение для гладкой и шероховатой поверхностей совпадают, что позволяет воспользоваться этими результатами.

В области переменные и в уравнении разделяются. Уравнение по является уравнением для свободной частицы и его решения можно взять в виде плоских волн , где - волновой вектор, параллельный плоскости решетки. Решения уравнения по в этой же области
могут быть в случае (убывающие со стороны решения) выбраны в виде
где , а в зависимости от либо блоховские волны вдоль оси , либо убывающие вглубь решетки поверхностные состояния. Функции непрерывны в точке и .
Общее решение уравнения представляется линейной комбинацией блоховских и поверхностных волн , а энергетический спектр электрона
определяется из условий сшивания волновой функции по на поверхности
В случае гладкой поверхности ( ) условие может выполняться, в том числе, и для чисто поверхностных волн [5]. Эти состояния существуют только при определенных значениях .
В случае шероховатой поверхности потенциал шероховатости смешивает состояния с разными и , что означает рассеяние поверхностного состояния.

Затухание поверхностного состояния
В соответствии с постановкой задачи представим волновую функцию электрона в виде
где - поверхностная волна, а - либо поверхностные волны, либо уходящие вглубь решетки блоховские волны, при этом
и
Энергию считаем вещественной. Как мы увидим, волновой вектор является комплексным, что отражает убывание амплитуды поверхностной волны в результате рассеяния. Такая ситуация не является реальной в случае неограниченной поверхности, но позволяет оценить затухание на единицу длины в области шероховатости.
Оценку затухания поверхностной волны проведем по теории возмущений, предложенной в [4]. Для этого условие на волновую функцию перепишем, явно выделив уравнение, содержащее , (учтено, что )

Здесь амплитуда Фурье потенциала шероховатости, а - размер
решетки по осям и .
Считая возмущение поверхностной волны малым, отбросим во втором уравнении системы члены второго порядка малости и учитывая, что
а
приходим к условию совместности системы
Это уравнение определяет волновые числа электронной поверхностной волны. Правая часть этого уравнения является комплексным числом в силу комплексности для блоховских волн и наличия нулей у знаменателя. В силу этого комплексными являются и волновые числа поверхностного состояния электрона. Мнимые добавки к волновому числу отражают затухание поверхностного состояния электрона вдоль шероховатой поверхности по сравнению со случаем гладкой поверхности. Кроме того, меняется и фазовая скорость поверхностной волны по сравнению со случаем гладкого интерфейса за счет добавки к вещественной части волнового числа .
Оценим затухание поверхностной электронной волны, усредненное по ансамблю реализаций поверхности со случайной шероховатостью. Поскольку нас интересует мнимая часть волнового числа, то суммирование можно вести только по области , соответствующей блоховским волнам, полюса же в этом уравнении учтем стандартным образом, обходя их по малой полуокружности в области комплексных .

Для дальнейшего анализа выберем в виде
где среднеквадратичная случайная добавка к мощности поверхностного потенциала ,
а -обратная корреляционная длина шероховатости. Кроме того, заменой
выполним в уравнении стандартный переход от суммирования по квазидискретным волновым векторам к интегрированию.
Для краткости записи введем обозначение:
После интегрирования по углам правая часть уравнения , которую обозначим , сводится к
где - функция Бесселя от мнимого аргумента первого рода.
Мнимая часть отрицательна и равна

В интеграле выполнена замена переменной и интегрирование по идет, как отмечалось, только по областям, отвечающим блоховским волнам, т.е. там где . Второе слагаемое есть вклад от полюсов ( ).
Считая затухание малым, в правую часть уравнения подставим значения , , отвечающие поверхностному состоянию для гладкой поверхности с мощностью потенциала поверхности . (Такой потенциал поверхности получается эффективно в пределе для уравнения с коррелятором и, кроме того, это позволяет избежать расходимости в полюсном члене в пределе ). Тогда правая часть уравнения (11) даст просто поправку к . С учетом этого находим поправки к ( )
и поправки к волновому числу (учтено, что )
.

Расчеты
Для расчетов выберем случай и . С учетом условия получаем, что . В области отрицательных имеется единственная «разрешенная» зона, отвечающая блоховским волнам , и для того, чтобы она давала вклад значение должно лежать выше этой зоны. Кроме того, в области отрицательных вклад от полюсов содержит только одно слагаемое, а условие ведет к тому, что лежит ниже разрешенной зоны .
На рис. показана зависимость от . Кроме того, отдельно показаны вклады в только от рассеяния вглубь решетки и только за счет рассеяния по поверхности.

Рис. а. Зависимость от при =3, =4.5 Рис. б. Зависимость от при =3, =4.5
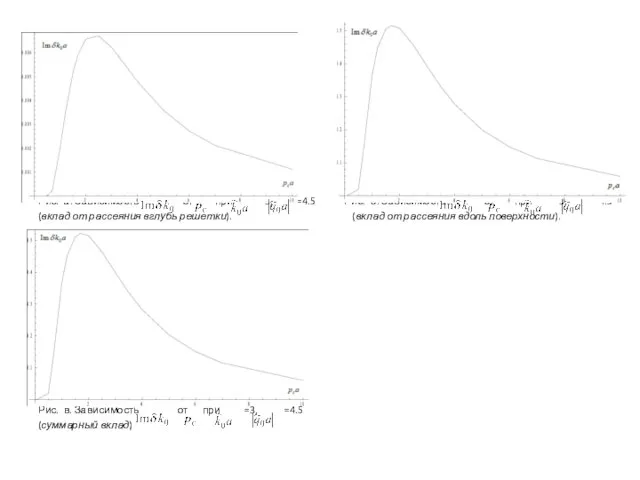
(вклад от рассеяния вглубь решетки). (вклад от рассеяния вдоль поверхности).
Рис. в. Зависимость от при =3, =4.5
(суммарный вклад)

Как видно из результатов расчетов коэффициент затухания мал как при , так и при , что физически оправдано. При большой корреляционной длине неровностей поверхности и малой длине поверхностной волны затухание мало, так как этот случай мало отличается от гладкой поверхности. В противоположном случае малой корреляционной длины неровностей и большой длины волны поверхностного состояния затухание также мало в силу сглаживания неровностей на расстояниях порядка длины волны, что опять ведет к случаю гладкой поверхности.
Кроме того, при выбранных значениях параметров задачи вклад в от рассеяния вглубь решетки сильно подавлен по сравнению с вкладом от рассеяния вдоль поверхности. Для выяснения причин этого проведем аналитические оценки первого и второго слагаемых. Интегрирование идет, как указывалось, по единственной «разрешенной» зоне в области отрицательных . Границы зоны определяются условиями . Приближенное решение этого уравнения для границ зоны дает
Откуда для ширины зоны находим
Оценивая интеграл в (14) по теореме о среднем с учетом того, что в средней точке интервала можно считать , находим

Оценка вклада второго слагаемого в (14) имеет вид
где учтено, что .
Как видим и имеют подобное поведение, как функции , но существенно разное поведение в зависимости от параметров потенциала сверхрешетки и потенциала поверхностного слоя . При выбранных при численных расчетах значениях параметров и отношение вкладов от рассеяния вглубь решетки и от рассеяния вдоль поверхности при составляет

Заключение
Проведен анализ влияния шероховатости границы сверхрешетки на поверхностные состояния электронов в простейшем однозонном приближении для невырожденных энергетических зон кристаллической решетки. Сверхрешетка моделировалась -образными потенциальными ямами, поверхностная потенциальная яма отличалась по глубине от остальных потенциальных ям сверхрешетки, а неровность поверхности вводилась через зависимость мощности потенциала поверхностного слоя от координат точек слоя.
Показано, что волновая функция усредненного поверхностного состояния будет затухать в направлении распространения вдоль граничной поверхности сверхрешетки в результате рассеяния на неровностях поверхности и преобразования поверхностной волны в объемные блоховские волны, уходящие вглубь решетки. Получены выражения для коэффициента затухания поверхностного состояния в продольном направлении, при этом выделены вклады, обусловленные рассеянием вдоль поверхности и рассеянием с преобразованием поверхностной волны в объемные волны, и проведены расчеты этого коэффициента.

Примечания
Функции имеют вид
Здесь - целая часть числа , - его дробная часть и
где