Содержание
- 2. Цели: Повторить и обобщить знания по теме «Арифметическая и геометрическая прогрессия». Расширить знания. Совершенствовать навыки решения
- 3. Домашнее задание Обязательный уровень: №391(а,б) № 427 №420(б, в) Уровень повышенной сложности: №425(а, г, д) №468
- 4. Учет результатов работы
- 5. I. Проверка теории
- 6. Заполненная таблица
- 8. Связь прогрессий an=an-1+d аn=an-1·d an=a1+d(n-1) an=a1·dn-1
- 9. Прогрессио – это …
- 10. II. Экспресс-опрос Вариант 2. I. Дано (bn ) : ½; 1; … - геометрическая прогрессия 1.
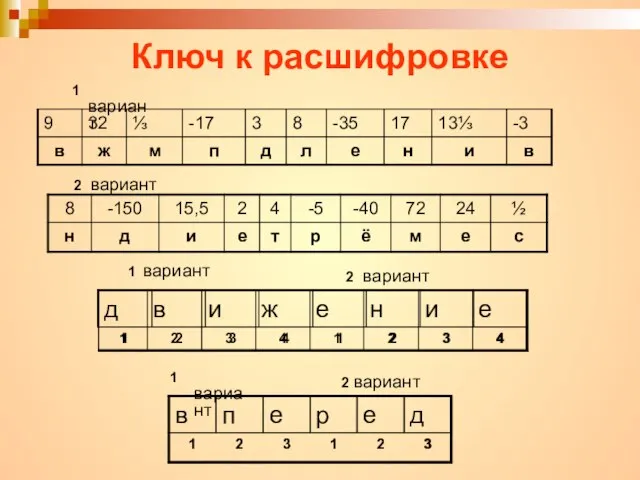
- 11. Ключ к расшифровке 1 вариант 2 вариант 1 вариант 1 вариант 2 вариант 2 вариант
- 13. Прогрессио – движение вперед! - будешь как я!
- 14. Из истории 5 век до н.э. – древние греки знают формулы суммы натуральных и четных натуральных
- 15. Сколько зерен попросил изобретатель шахмат у царя? Ответ : 18 квинтиллионов 500 квадриллионов.
- 16. Задача из ЕГЭ Юноша подарил девушке в первый день 3 цветка, а в каждый последующий день
- 18. Решение 1. Пусть (кол-во цветов, купленных в 1-ый день), тогда (на столько юноша увеличивал каждый день
- 19. III. Тест-прогноз Вариант I. В геометрической прогрессии (cn) c2=8, c4=2. 1. Найдите знаменатель прогрессии. (1балл) 2.
- 20. Тест-прогноз. Ответы:
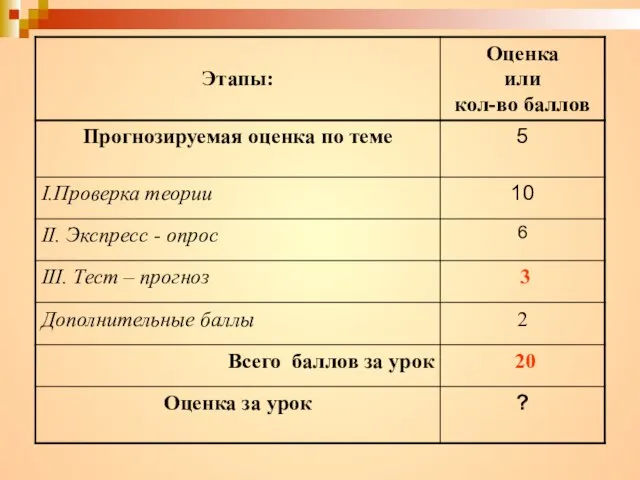
- 22. Итоги Критерии оценки
- 23. Решение первой задачи Дано: (сn) – геом. прогрессия с2 = 8; с4 = 2 Найти: q
- 24. Решение второй задачи Дано: (сn) – геом. прогрессия с2 = 8; q1 = ½; q2 =
- 25. Решение третьей задачи вариант 1 Дано: (сn ) – геом. прогрессия с1 = -16; q =
- 26. Решение третьей задачи вариант 2 Дано: (bn) – геом. прогрессия b1 = 27; q = ⅓
- 28. Скачать презентацию























 Lluvia
Lluvia Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах
Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах УД ПСИХОЛОГИЯ
УД ПСИХОЛОГИЯ Храмы России
Храмы России Оптическая микроскопия
Оптическая микроскопия Менеджмент
Менеджмент Кондитерский отдел
Кондитерский отдел Органы и службы стандартизации РФ
Органы и службы стандартизации РФ Вышел зайчик погулять Художник – В. Сергеев
Вышел зайчик погулять Художник – В. Сергеев Знакомство с точкой
Знакомство с точкой Состояние и задачи управления проектами в строительстве
Состояние и задачи управления проектами в строительстве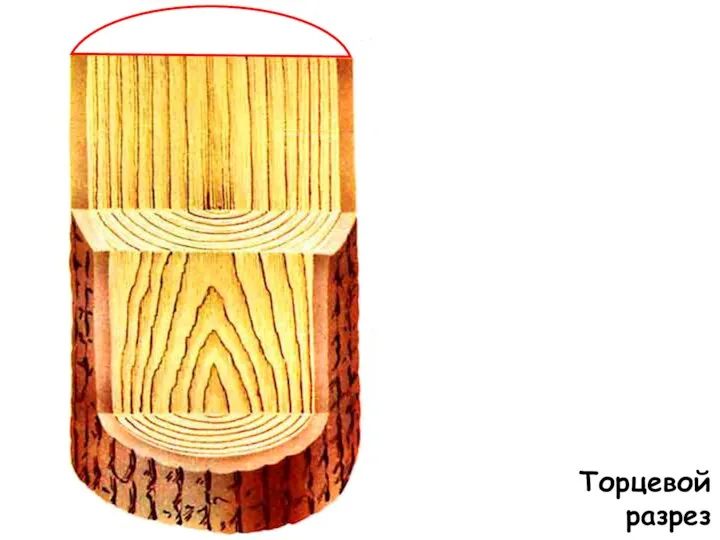 Торцевой разрез. Материаловедение
Торцевой разрез. Материаловедение чайные истории
чайные истории Шпаргалка юного покупателя
Шпаргалка юного покупателя Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор
Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор Классификация реакций
Классификация реакций Организация хранения документов Архивного фонда Российской Федерации и других архивных документов
Организация хранения документов Архивного фонда Российской Федерации и других архивных документов Трансляция – биосинтез белка на рибосоме
Трансляция – биосинтез белка на рибосоме Инновационный подход к жизни
Инновационный подход к жизни DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D
DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D Урок – размышление по рассказу К.Г. Паустовского «Телеграмма»
Урок – размышление по рассказу К.Г. Паустовского «Телеграмма» Путешествие в мир животных
Путешествие в мир животных СПАСИБО, АЗБУКА!
СПАСИБО, АЗБУКА! Rave Cosmology Today Dying, Death & Bardo . RC3.8
Rave Cosmology Today Dying, Death & Bardo . RC3.8 Основные закономерности развития информационного пространства
Основные закономерности развития информационного пространства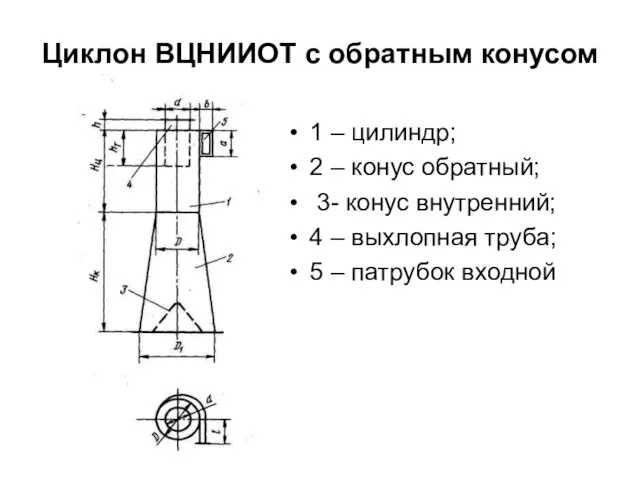 Циклон ВЦНИИОТ с обратным конусом
Циклон ВЦНИИОТ с обратным конусом  Квантовые компьютеры
Квантовые компьютеры Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)
Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)