Содержание
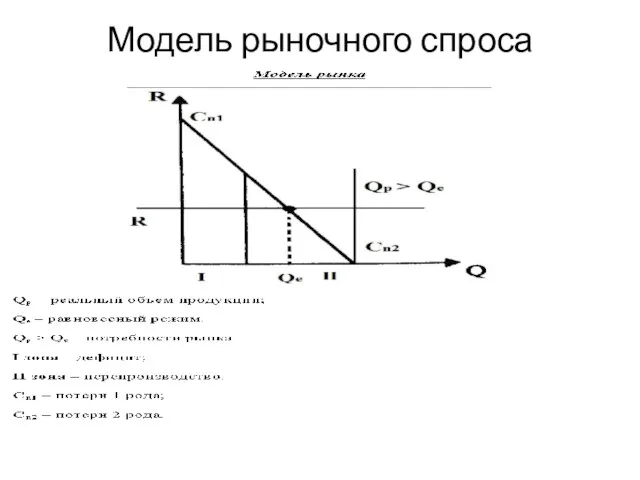
- 2. Модель рыночного спроса
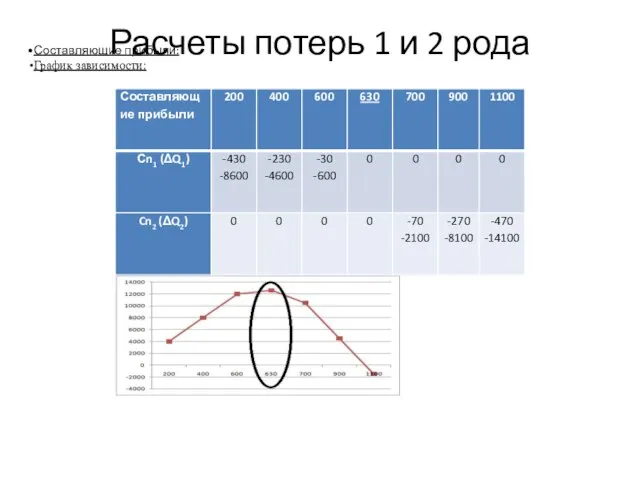
- 3. Оценки потерь двух видов Δ Q1 = Qe - Qp – недопроизводство => потери от дефицита
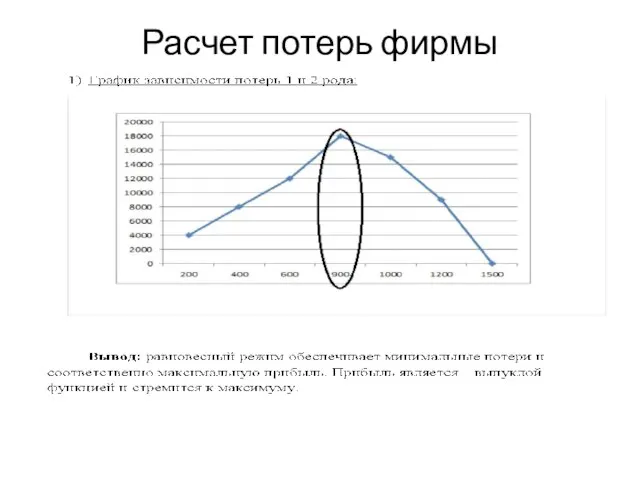
- 4. Формализация цели фирмы Определим цель фирмы Цель фирмы: B (Qр) => max, где: В – прибыль.
- 5. Исходные данные Условие задачи: Фирма работает на рынке с функцией спроса Q = (1000+(10n)) – 6pv,
- 6. Определение равновесного режима Решение: Вычисляем удельную прибыль - маржу (m) m = pv - pr =
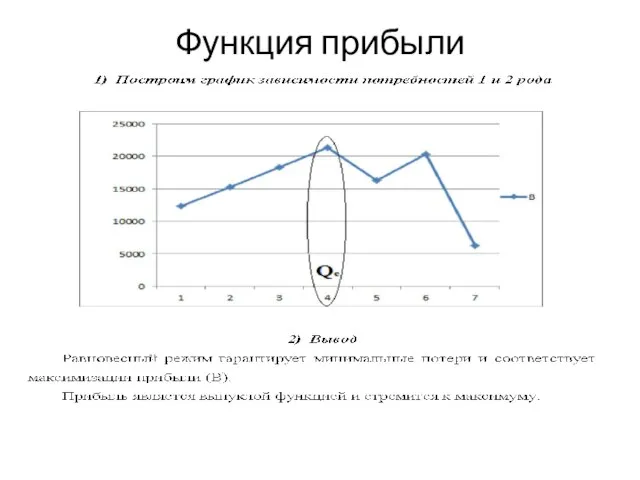
- 7. Функция прибыли
- 8. Адаптация к росту спроса на 20%
- 9. Решения менеджера 4) Вычислим количество продукции (Q)для равновесного режима рынка Q = a – b*pv 1068
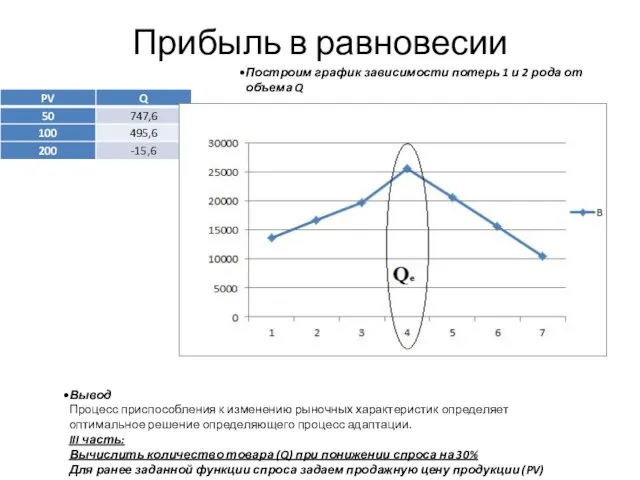
- 10. Прибыль в равновесии Построим график зависимости потерь 1 и 2 рода от объема Q Вывод Процесс
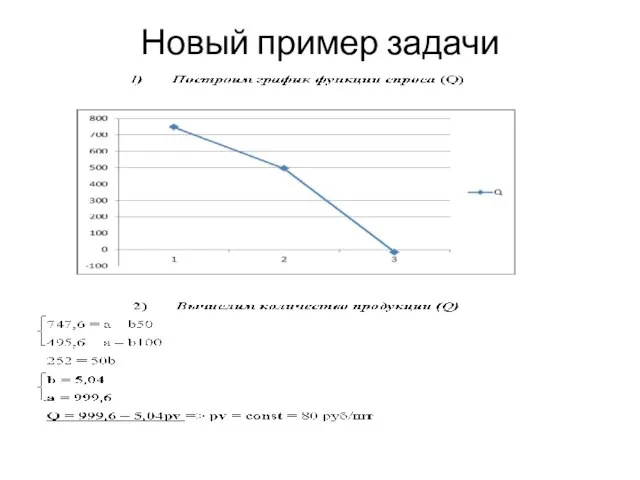
- 11. Новый пример задачи
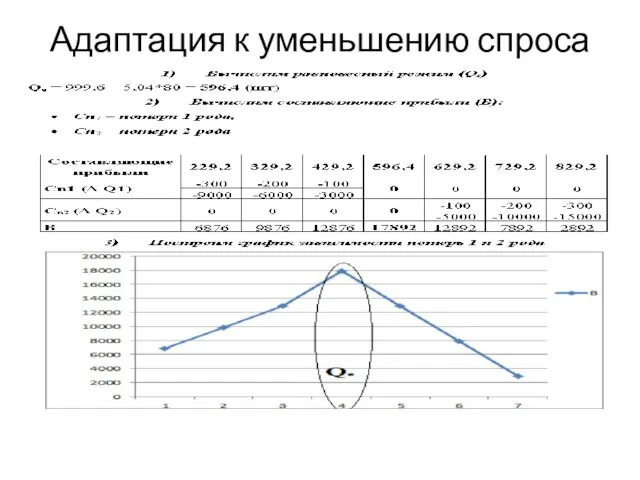
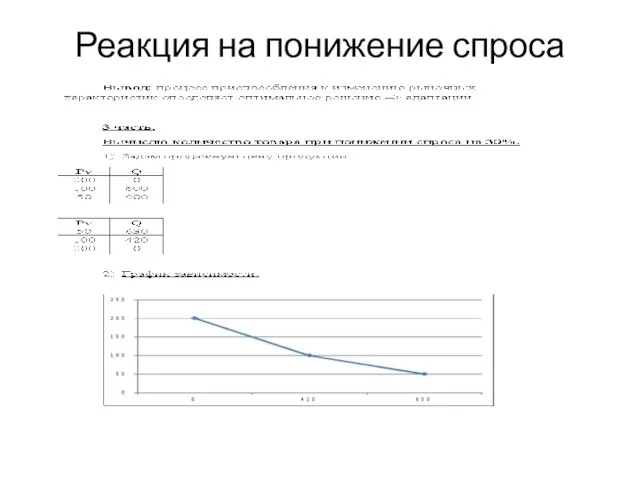
- 12. Адаптация к уменьшению спроса
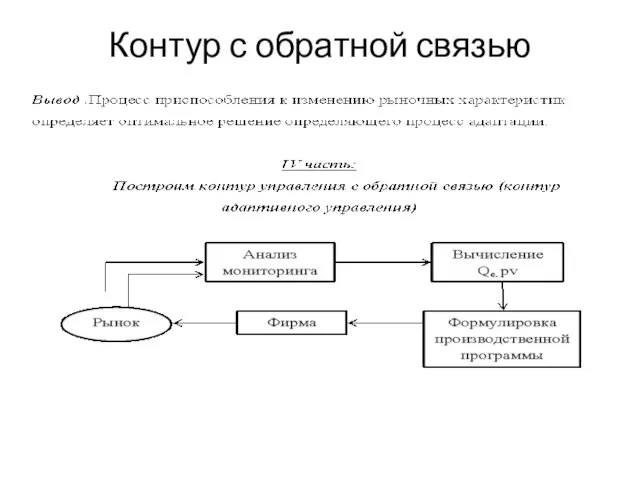
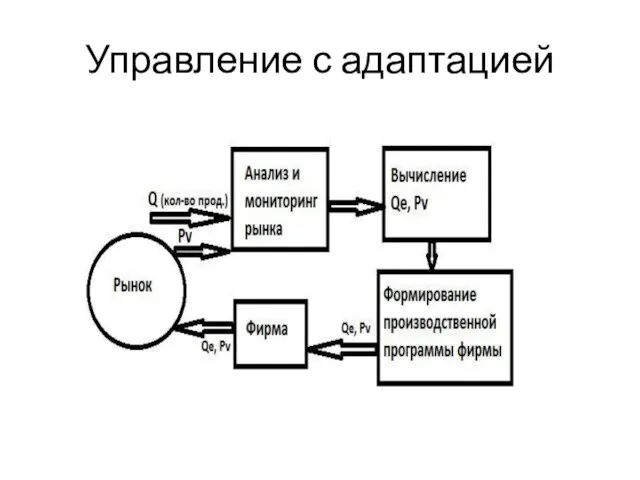
- 13. Контур с обратной связью
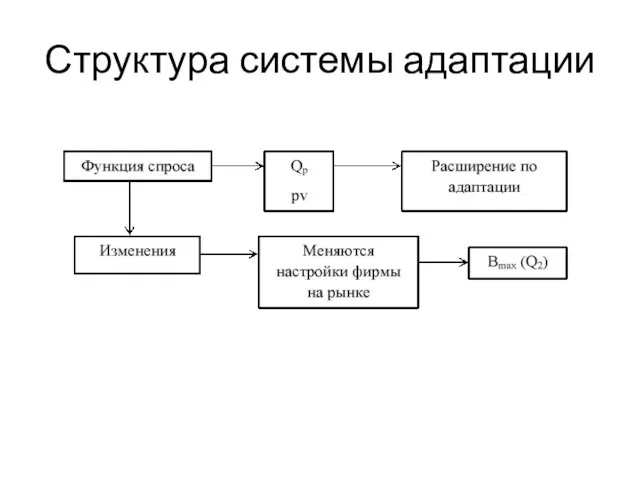
- 14. Структура системы адаптации
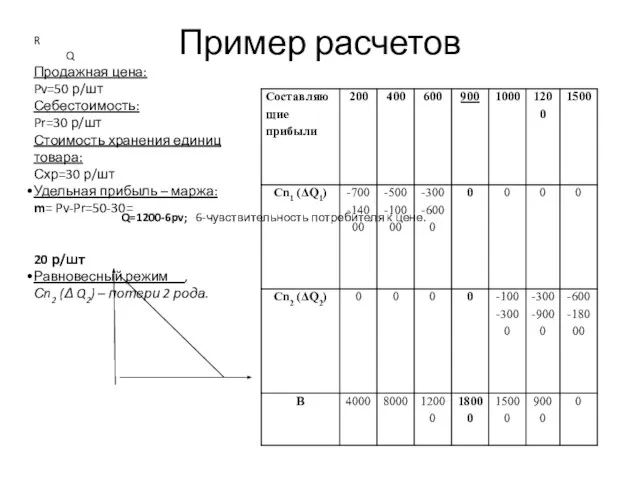
- 15. Пример расчетов Q=1200-6pv; 6-чувствительность потребителя к цене. R Q Продажная цена: Pv=50 р/шт Себестоимость: Pr=30 р/шт
- 16. Расчет потерь фирмы
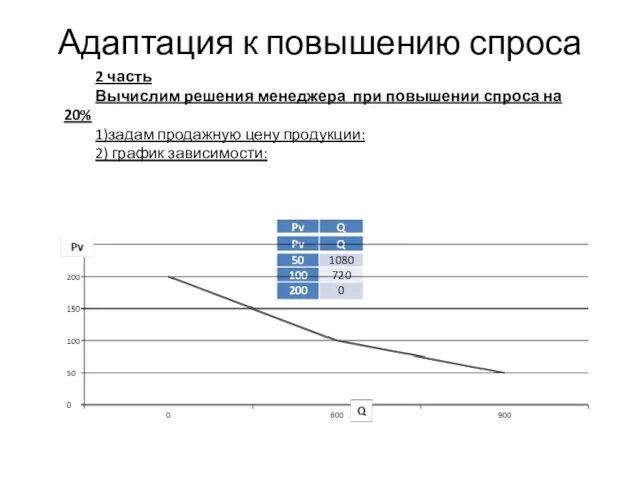
- 17. Адаптация к повышению спроса 2 часть Вычислим решения менеджера при повышении спроса на 20% 1)задам продажную
- 18. Решения менеджера 3) вычислим количество продукции, реализуемой для максимума прибвли: Q = a – b*pv 1080
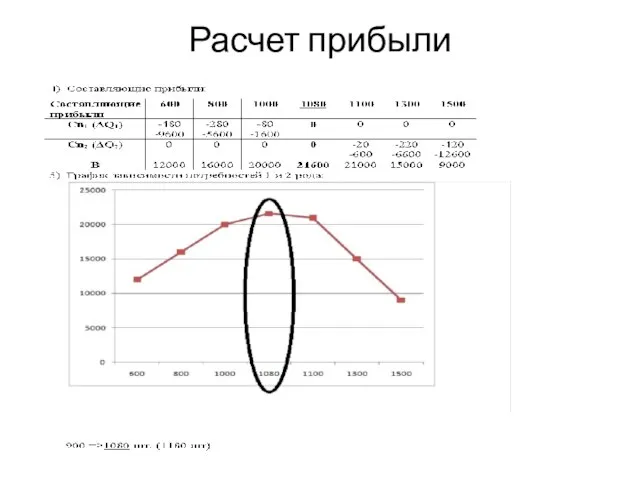
- 19. Расчет прибыли
- 20. Реакция на понижение спроса
- 21. Оптимальные решения Вычисляем оптимальное количество производимой продукции: 630 = а – b50 0 = a –
- 22. Расчеты потерь 1 и 2 рода Составляющие прибыли: График зависимости:
- 23. Управление с адаптацией
- 24. Вывод формул расчета Qp- реальный объем Qe-равновесный режим △Q1=Qe-Qp-недопроизводство(потери от дефицита) △Q2=Qp-Qe-размер перепроизводства △Q=0 (Qp=Qe) -
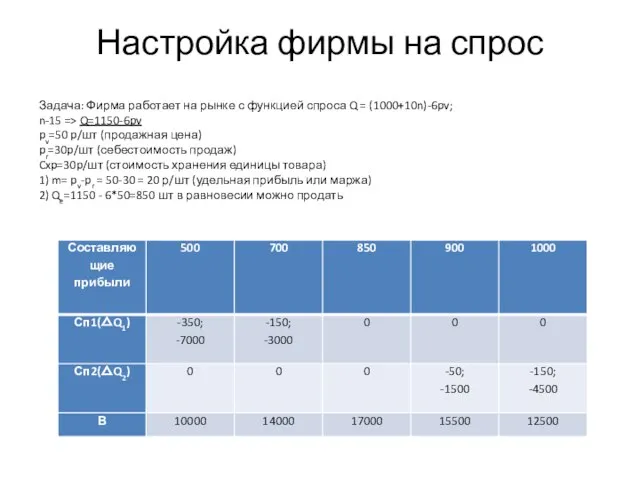
- 25. Настройка фирмы на спрос Задача: Фирма работает на рынке с функцией спроса Q = (1000+10n)-6pv; n-15
- 26. Пример решения задачи адаптации Фирма работает на рынке с функцией спроса: Q=(1000+10n)-6 Pv, где n=23, Q=1230-6
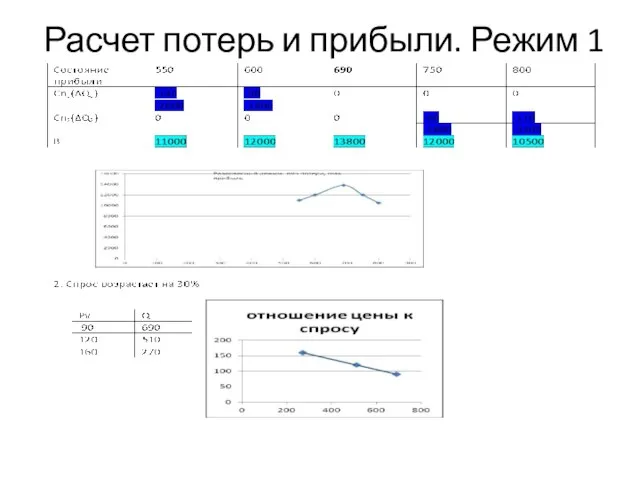
- 27. Расчет потерь и прибыли. Режим 1
- 28. Расчет потерь и прибыли. Режим 2.
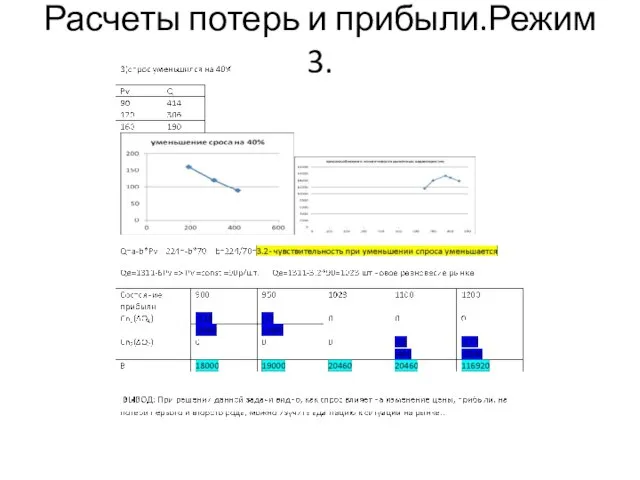
- 29. Расчеты потерь и прибыли.Режим 3.
- 30. Задание 17.1. Для любого интересующего Вас рынка: -определить таблицу связи p и Q Построить график и
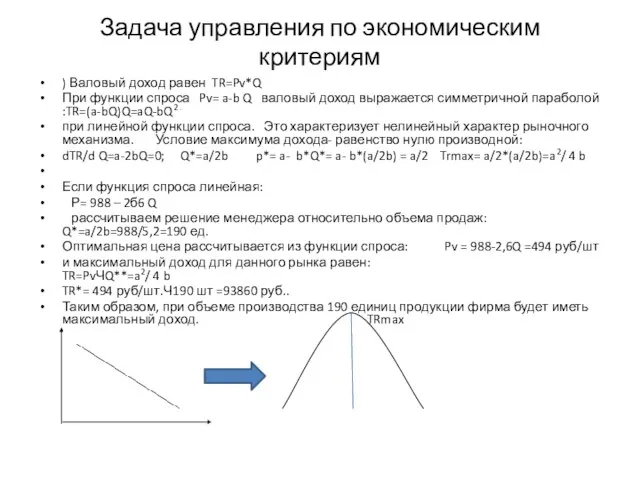
- 31. Задача управления по экономическим критериям ) Валовый доход равен TR=Pv*Q При функции спроса Pv= a-b Q
- 32. Обеспечение максимального дохода
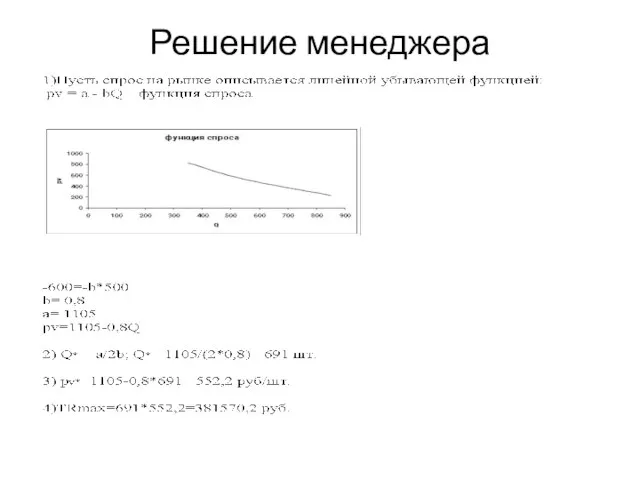
- 33. Решение менеджера
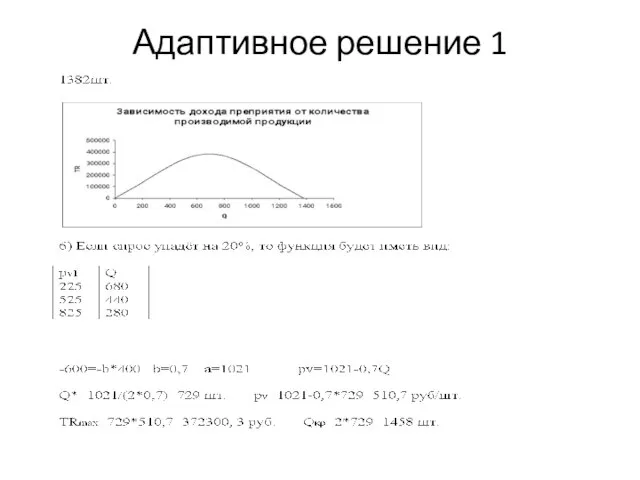
- 34. Адаптивное решение 1
- 35. Адаптивное решение 2
- 37. Скачать презентацию














 Секция «Проектирование учебного плана и программ дисциплин в области начального образования
Секция «Проектирование учебного плана и программ дисциплин в области начального образования Июль 2007
Июль 2007 Район Отрадное. Слайды
Район Отрадное. Слайды Презентация на тему Природные источники углеводородов
Презентация на тему Природные источники углеводородов  Бюджет семьи
Бюджет семьи Презентация на тему: Подходы, методы и инструментарий формирования готовности к самостоятельному определению профессиональных п
Презентация на тему: Подходы, методы и инструментарий формирования готовности к самостоятельному определению профессиональных п Мой друг, отчизне посвятимДуши прекрасные порывы! А.С. Пушкин
Мой друг, отчизне посвятимДуши прекрасные порывы! А.С. Пушкин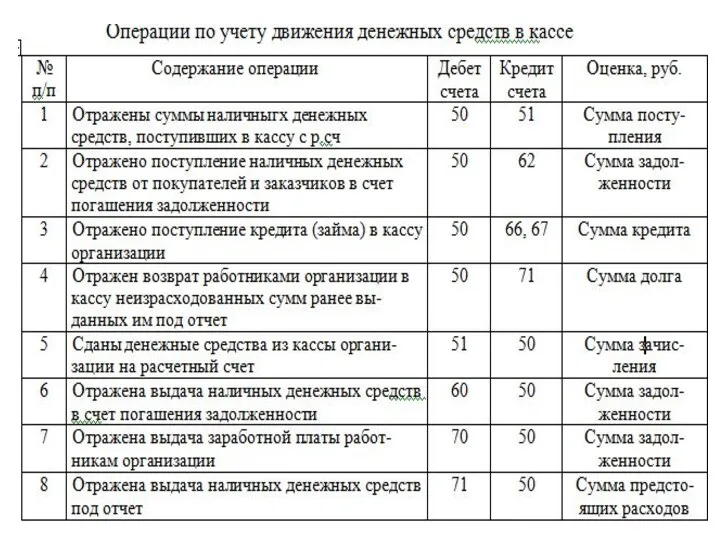 Операции по учету движения денежных средств в кассе
Операции по учету движения денежных средств в кассе Вниманию субъектов предпринимательства!
Вниманию субъектов предпринимательства! Перспективы развития информационных технологий в библиотечной сфере Хабаровского края
Перспективы развития информационных технологий в библиотечной сфере Хабаровского края Совещание с ответственными за планирование и результаты инновационной деятельности в образовательных учреждениях ЮЗАО
Совещание с ответственными за планирование и результаты инновационной деятельности в образовательных учреждениях ЮЗАО Презентация на тему история Крымской войны
Презентация на тему история Крымской войны  Искусство общения
Искусство общения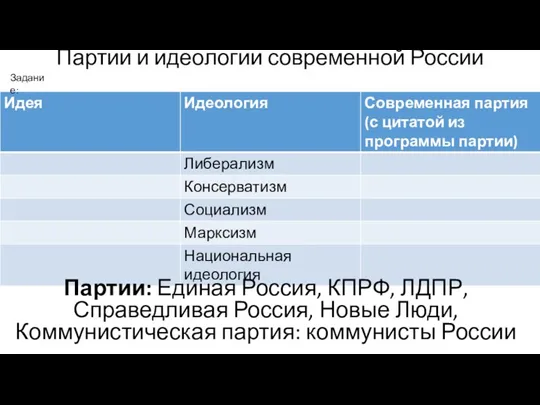 Партии и идеологии современной России
Партии и идеологии современной России STRATEGIC VISION AND 2007/08 ACADEMIC YEAR Марина ЛАТУХА Старший преподаватель кафедры организационного поведения и управления персоналом Высшая шк
STRATEGIC VISION AND 2007/08 ACADEMIC YEAR Марина ЛАТУХА Старший преподаватель кафедры организационного поведения и управления персоналом Высшая шк Дата открытия музея – 01.09.1983 год. Музей создавался по инициативе ветеранов II механизированного корпуса, при поддержке директора Г
Дата открытия музея – 01.09.1983 год. Музей создавался по инициативе ветеранов II механизированного корпуса, при поддержке директора Г Симметрия в цветочном мире
Симметрия в цветочном мире Виды изобразительного искусства
Виды изобразительного искусства Дания
Дания Творчество Б. Акунина
Творчество Б. Акунина Презентация на тему Домашние животные. Кто где живет?
Презентация на тему Домашние животные. Кто где живет?  Философско-методологические проблемы естествознания
Философско-методологические проблемы естествознания Разминка: определите вид химической связи HNO 3 Cl 2 KHSO 4 H2O H2O NaOH CaO Cu.
Разминка: определите вид химической связи HNO 3 Cl 2 KHSO 4 H2O H2O NaOH CaO Cu. «В Петербурге жила когда-то очаровательная женщина. Такая очаровательная, что я не знаю ни одного живого существа, не отдавшего ей
«В Петербурге жила когда-то очаровательная женщина. Такая очаровательная, что я не знаю ни одного живого существа, не отдавшего ей  我的朋友去外国旅游
我的朋友去外国旅游 Вы планируете провести масштабное конгрессное мероприятие (коллегию, конференцию, «круглый стол», семинар и т.п.) с приглашением ру
Вы планируете провести масштабное конгрессное мероприятие (коллегию, конференцию, «круглый стол», семинар и т.п.) с приглашением ру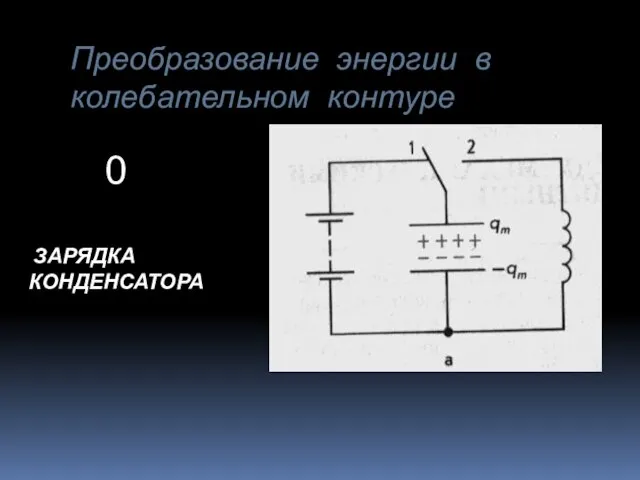 Презентация на тему Преобразование энергии в колебательном контуре
Презентация на тему Преобразование энергии в колебательном контуре  Ученическая научная конференция юных филологов «Дебют - 2011»
Ученическая научная конференция юных филологов «Дебют - 2011»