Содержание
- 2. Выполнила Учитель информатики и математики Кончева Оксана Юрьевна г.Дальнереченск
- 3. Преобразования на плоскости Подобие Движение начало конец
- 4. Определение и примеры гомотетия
- 5. При этом преобразовании расстояние между точками меняется в одно и то же число раз X X’
- 6. О – центр гомотетии OX’=kOX
- 7. Движение Определение Симметрия относительно прямой Симметрия относительно точки Поворот Параллельный перенос Симметрия в природе и на
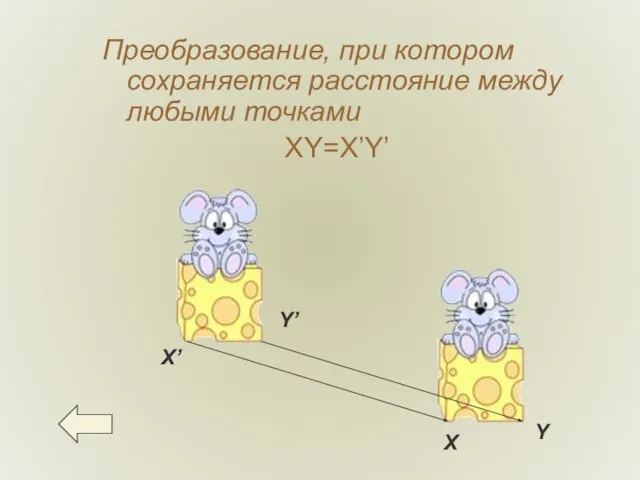
- 8. Преобразование, при котором сохраняется расстояние между любыми точками XY=X’Y’
- 9. Осевая симметрия Точка Х симметрична точке X’ относительно прямой а а – ось симметрии a
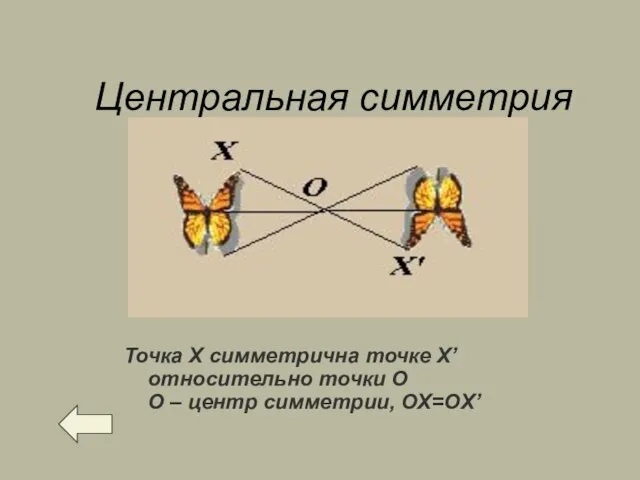
- 10. Центральная симметрия Точка Х симметрична точке X’ относительно точки О О – центр симметрии, ОХ=ОX’
- 11. поворот Точка Х переходит в точку Х’ Ŀа – угол поворота
- 12. Параллельный перенос Точка Х(х,у) переходит в точку Х’(x+a,y+b), где a и b одни и те же
- 14. Скачать презентацию









 Создание и форматирование документов Word
Создание и форматирование документов Word Страхование КАСКО и ОСАГО легковых, грузовых автомобилей, а так же другой спецтехники
Страхование КАСКО и ОСАГО легковых, грузовых автомобилей, а так же другой спецтехники Жизненный цикл папоротника
Жизненный цикл папоротника 20161218_chtogde_kogda
20161218_chtogde_kogda КЕЙС-СТАДИ ПО ЭФФЕКТИВНОМУ ИСПОЛЬЗОВАНИЮ ВИДЕОРЕКЛАМЫ В СЕТИ ИНТЕРНЕТ*
КЕЙС-СТАДИ ПО ЭФФЕКТИВНОМУ ИСПОЛЬЗОВАНИЮ ВИДЕОРЕКЛАМЫ В СЕТИ ИНТЕРНЕТ* Энурез – небольшая проблема для человечества, но огромная проблема для ребенка!
Энурез – небольшая проблема для человечества, но огромная проблема для ребенка! Россия: Разработка продуктов или аутсорсинг?
Россия: Разработка продуктов или аутсорсинг? Методы изучения генетики человека
Методы изучения генетики человека Презентация к урокуокружающий мир1 класс по теме: «Явления природы»(по курсу В. А. Самкова)
Презентация к урокуокружающий мир1 класс по теме: «Явления природы»(по курсу В. А. Самкова) Всё про воздух
Всё про воздух Общие основы психологии
Общие основы психологии Создание единого китайского государства
Создание единого китайского государства РУССКИЕ ПИСАТЕЛИ XX ВЕКА О РОДНОЙ ПРИРОДЕ
РУССКИЕ ПИСАТЕЛИ XX ВЕКА О РОДНОЙ ПРИРОДЕ Дед Мороз
Дед Мороз Научно-практическая конференция по математике Банковские кредиты. Мухаметшина Элина 5М 2013 год
Научно-практическая конференция по математике Банковские кредиты. Мухаметшина Элина 5М 2013 год CLIMATE OF THE UNITED KINGDOM
CLIMATE OF THE UNITED KINGDOM  Осеннее дерево (штампография)
Осеннее дерево (штампография) Физический калейдоскоп
Физический калейдоскоп How do we speak?
How do we speak? Деньги Money
Деньги Money Комплексное решение для вашего бизнеса
Комплексное решение для вашего бизнеса Шаблон "Фиолетовый снег"
Шаблон "Фиолетовый снег" Новое похождения выпускников, или удивительное путешествие по океану знаний
Новое похождения выпускников, или удивительное путешествие по океану знаний Транспорт
Транспорт НИУ
НИУ Запрет повторного осуждения
Запрет повторного осуждения Адронная терапия в мире
Адронная терапия в мире Публичная защита портфолио как форма представления результатов педагогической деятельности преподавателя школы искусств
Публичная защита портфолио как форма представления результатов педагогической деятельности преподавателя школы искусств