през Л4

ЗСИ и другие законы сохранения

Работа и кинетическая энергия

Работа и КЭ при криволинейном движении

Консервативные силы

Примеры консервативных сил (1)

Примеры консервативных сил (2)
любые центральные силы

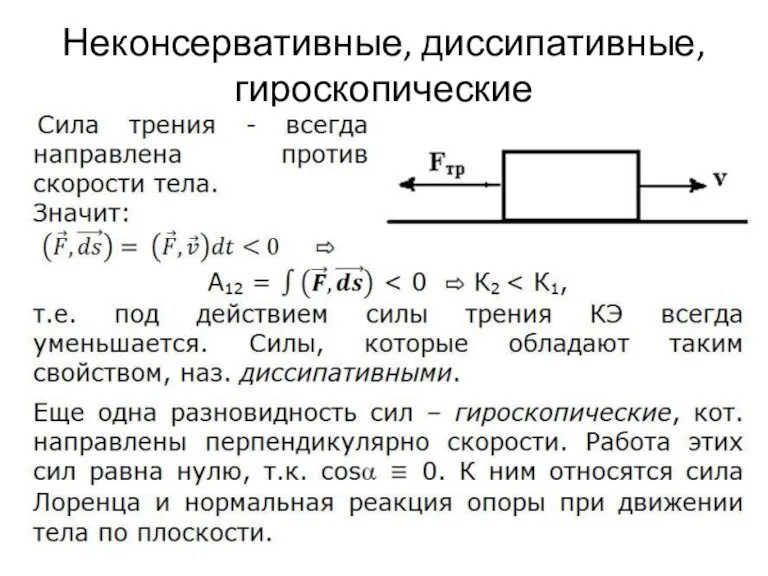
Неконсервативные, диссипативные, гироскопические

Потенциальная энергия

Свойства потенциальной энергии

ЗСПМЭ для материальной точки

ЗСПМЭ для системы материальных точек

Закон сохранения и изменения полной механической энергии
Если не все силы, действующие на систему МТ или внутри нее, консервативные, то ПМЭ системы меняется на величину работы неконсервативных сил Анк:
∆Е = ∆U + ∆К = Анк,
или Е2 – Е1 = U2 – U1 + К2 – К1 = А12нк
Это соотношение выражает закон сохранения и изменения ПМЭ системы.
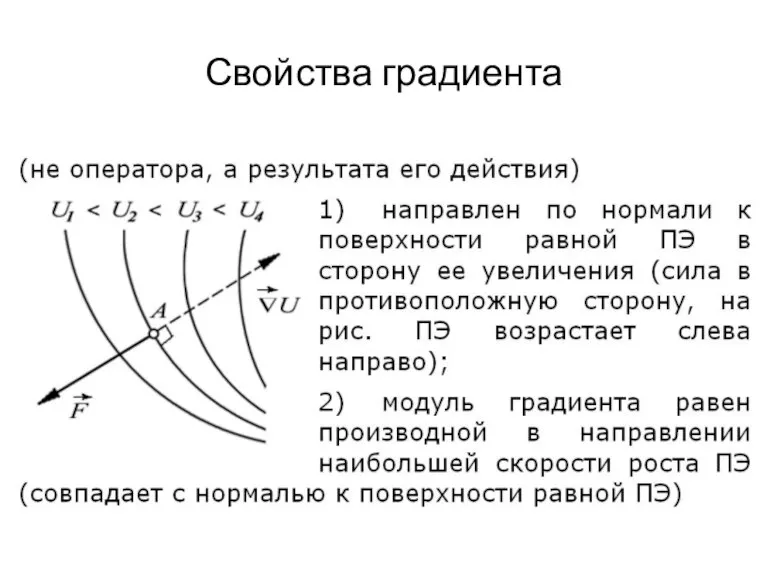
Для чего вводилось понятие о ПЭ?
Во-1, с его помощью формулируется закон сохранения и изменения ПМЭ ⇨ упрощает решение динамических уравнений движения.
Во-2, знание ПЭ ↓ объем сведений, нужных для составления этих уравнений движения.

ПЭ и сила

Частная производная

Оператор градиента

Свойства градиента

Пример связи ПЭ и силы (1)