Содержание
- 2. Фи́зика твёрдого те́ла Фи́зика твёрдого те́ла — раздел физики конденсированного состояния, задачей которого является описание физических
- 3. Для начала вспомним, что в обычных условиях все объекты окружающие нас находятся в трех основных агрегатных
- 4. Геометрически правильная внешняя форма кристаллов, образующихся в природных или лабораторных условиях, натолкнула ученых ещё в семнадцатом
- 5. В 2000 году на севере Мексики на глубине порядка 300 метров под горой Найка (здесь в
- 7. Кристаллофизика Кристаллы многих минералов и драгоценных камней были известны и описаны ещё несколько тысячелетий назад. Одна
- 8. Криста́ллы (от греч. κρύσταλλος, первоначально — лёд, в дальнейшем — горный хрусталь, кристалл) — твёрдые тела,
- 9. Внешне особенность кристалла выражается в окаймлении кристаллов плоскими гранями, которые пересекаются по прямым рёбрам. У разных
- 10. Одним из учёных, открывших закон, объясняющий это сходство, – закон постоянства углов в кристаллах – был
- 11. При росте кристалла в зависимости от ряда случайностей одни грани могут попасть в условия более благоприятные,
- 12. Евграф Степанович Фёдоров (1853— 1919) — русский кристаллограф, минералог и математик. Крупнейшее достижение Е. С. Фёдорова
- 13. Е.С. Фёдоров не только указал на возможность определения вещества по форме кристалла, но и составил вместе
- 14. Симметрия На рисунке правая часть скульптуры в точности совпадёт с отражением левой её части. Эта симметричная
- 15. На рисунке изображена детская бумажная вертушка. Она тоже симметрична, но плоскость симметрии через неё провести нельзя.
- 16. Фигура обладает симметрией, если существует движение (преобразование не тождественное), переводящее ее в себя. К фундаментальным понятиям
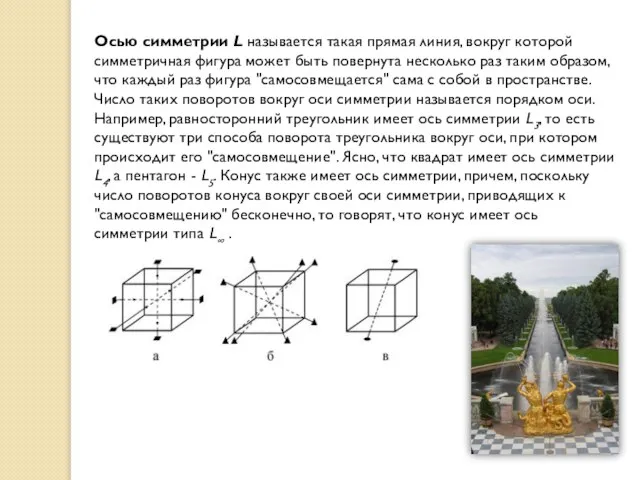
- 17. Осью симметрии L называется такая прямая линия, вокруг которой симметричная фигура может быть повернута несколько раз
- 18. Наконец, центром симметрии C называется такая особая точка внутри фигуры, характеризующаяся тем, что любая проведенная через
- 19. Чтобы понять, что такое трансляционная симметрия, нам придётся поговорить… об обоях. Посмотрите на рисунок . На
- 20. Симметрия широко встречается в объектах живой и неживой природы. Например, симметрия в химии отражается в геометрической
- 21. Какое же отношение имеют обои к кристаллу? Каждое тело, в том числе и кристалл, состоит из
- 22. Структура кристалла – это пространственное расположение его атомов (или молекул). Если с каждой группой атомов(молекул) связать
- 23. Существуют простые кристаллы, построенные из атомов одного сорта. Например, алмаз – это чистый углерод. Кристаллы поваренной
- 24. Основная особенность кристаллической структуры заключается в её повторяемости через строго одинаковые расстояния. Предположим, что мы сделали
- 25. Гранецентрированная Объёмно-центрированная Базо-центрированная Примитивная Решетка Браве является математической моделью, отражающей трансляционную симметрию кристалла. Все многообразие кристаллов
- 26. Решетка Браве является математической моделью, отражающей трансляционную симметрию кристалла. В общем случае, решётка Браве не совпадает
- 27. В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на ряд кристаллических систем. По форме элементарной
- 28. ромбическая сингония — три прямых угла нет осей одинаковой длины; гексагональная сингония — две оси одинаковой
- 29. Сэр Уильям Генри Брэгг( 1862-1942) — английский физик, лауреат Нобелевской премии по физике за 1915 г.
- 30. Толкование рентгеновской дифракционной картины, полученной в опыте Лауэ, оказалось довольно сложным, и разрешили эту проблему независимо
- 31. Простейший случай Брэгговской дифракции возникает при рассеянии видимого света на дифракционной решётке. Аналогичное явление наблюдается при
- 32. Важной датой в истории физики твердого тела является 8 июня 1912 года. В этот день в
- 33. Макс фон Лауэ (1879 — 1960) — немецкий физик, лауреат Нобелевской премии по физике в 1914
- 34. Пе́тер Йо́зеф Вильге́льм Деба́й (1884— 1966) — голландский физик, лауреат Нобелевской премии по химии за 1936
- 36. Скачать презентацию
Слайд 2Фи́зика твёрдого те́ла
Фи́зика твёрдого те́ла — раздел физики конденсированного состояния, задачей которого является
Фи́зика твёрдого те́ла
Фи́зика твёрдого те́ла — раздел физики конденсированного состояния, задачей которого является

Интенсивно развивалась в XX веке после открытия квантовой механики. Развитие стимулировалась широким спектром важных задач прикладного характера, в частности, развитием полупроводниковой техники.
В настоящее время физика твёрдого тела разбилась на большое количество более мелких направлений.
Слайд 3Для начала вспомним, что в обычных условиях все объекты окружающие нас находятся
Для начала вспомним, что в обычных условиях все объекты окружающие нас находятся

В свою очередь все твердые тела можно разделить на две большие категории: аморфные и кристаллические тела. К аморфным веществам относятся стекла, твердые смолы и т д., а к кристаллическим веществам относятся, например, поваренная соль, медный купорос, графит и тд.
Кристаллические тела (кристаллы) — это твердые тела, в которых атомы расположены в соответствии с определенным правилом и образуют дальний порядок.
Это значит, что в кристаллах атомы образуют периодически повторяющуюся последовательность вдоль направлений пространственных осей. У аморфных тел дальний порядок отсутствует.
Слайд 4Геометрически правильная внешняя форма кристаллов, образующихся в природных или лабораторных условиях, натолкнула
Геометрически правильная внешняя форма кристаллов, образующихся в природных или лабораторных условиях, натолкнула

При росте кристалла в идеальных условиях форма его в течение всего роста остается неизменной, как если бы к растущему кристаллу непрерывно присоединялись бы элементарные кирпичики. Сейчас известно, что такими элементарными кирпичиками являются атомы или группы атомов. Кристаллы состоят из атомных рядов, периодически повторяющихся в пространстве и образующих кристаллическую решетку
Слайд 5В 2000 году на севере Мексики на глубине порядка 300 метров под
В 2000 году на севере Мексики на глубине порядка 300 метров под

Слайд 7Кристаллофизика
Кристаллы многих минералов и драгоценных камней были известны и описаны ещё несколько
Кристаллофизика
Кристаллы многих минералов и драгоценных камней были известны и описаны ещё несколько

Одна из наиболее ранних зарисовок кристаллов содержится в китайской фармакопее одиннадцатого века нашей эры. Кристаллы кварца из императорской короны, сохранившиеся с 768 года нашей эры, находятся в Сёсоине, сокровищнице японских императоров в Нара. Кристаллом называли вначале только лёд, а затем и кварц, считавшийся окаменевшим льдом. В конце эпохи средневековья слово «кристалл» стало употребляться в более общем смысле.
Слайд 8Криста́ллы (от греч. κρύσταλλος, первоначально — лёд, в дальнейшем — горный хрусталь, кристалл) — твёрдые
Криста́ллы (от греч. κρύσταλλος, первоначально — лёд, в дальнейшем — горный хрусталь, кристалл) — твёрдые

Кристаллы — это твёрдые вещества, имеющие естественную внешнюю форму правильных симметричных многогранников, основанную на их внутренней структуре, то есть на одном из нескольких определённых регулярных расположений, составляющих вещество частиц (атомов, молекул, ионов).
В 1892 году Даниель Сваровски изобрел автоматическую ограночную машину. В 1895 году им была основана компания Swarovski, и его машину впервые установили на ограночную фабрику в Ваттенс — здесь он мог использовать в своих интересах местную гидроэлектростанцию для энергоёмких процессов размола и переработки хрусталя.
Слайд 9Внешне особенность кристалла выражается в окаймлении кристаллов плоскими гранями, которые пересекаются по
Внешне особенность кристалла выражается в окаймлении кристаллов плоскими гранями, которые пересекаются по

Рассмотрим внимательно большое количество кристаллов одного и того же вещества. Не все образцы будут представлять собой правильные фигуры. Некоторые кристаллики будут просто обломками, другие будут иметь одну, две грани «ненормально» развитыми. Однако ряд образцов покажется нам достаточно идеальным. Отберём их из общей кучи и зарисуем. Мы увидим тогда, что имеются кристаллы, отличающиеся друг от друга главным образом размером. Если маленький пропорционально увеличить, то он будет в точности повторять большой. Наряду с такими кристалликами мы найдём и другие, чем-то похожие друг на друга, но уже не совпадающие ни при каком пропорциональном изменении размеров.
Слайд 10Одним из учёных, открывших закон, объясняющий это сходство, – закон постоянства углов в
Одним из учёных, открывших закон, объясняющий это сходство, – закон постоянства углов в

Посмотрите на рисунок, где изображён ряд кристаллов кварца. Все эти кристаллики – близкие родственники. Их можно сделать и совсем одинаковыми, сошлифовывая грани на различную глубину параллельно самим себе. Легко видеть, что таким способом, например, кристалл II может быть сделан совершенно таким же, как кристалл I. Эта возможность следует из того замечательного обстоятельства, что углы между сходственными гранями образцов одинаковы, например, между гранями А и Б, Б и В и т.д
В этом равенстве углов и заключается «семейное» сходство кристаллов. При сошлифовывании граней параллельно самим себе форма кристалла изменяется, но углы между гранями сохраняют своё значение
Слайд 11При росте кристалла в зависимости от ряда случайностей одни грани могут попасть
При росте кристалла в зависимости от ряда случайностей одни грани могут попасть

Кристалл вырастет неправильным, родственные взаимоотношения между выросшими в разных условиях образцами станут незаметными, но углы между сходственными гранями всех кристаллов изучаемого вещества будут всегда одинаковы. Форма кристалла случайна, а углы между гранями отвечают (и мы дальше поймём, почему) его внутренней природе.
Этот очень важный закон природы помогает нам узнавать, с каким веществом мы имеем дело. Два образца могут быть внешне очень непохожими, но если измерение показывает, что углы между гранями одинаковы, то имеются серьёзные основания полагать, что мы имеем дело с одним и тем же веществом. Напротив, отсутствие совпадающих углов между гранями говорит за то, что кристаллы принадлежат разным веществам.
Анализ вещества, построенный на этой идее, был разработан творцом современной кристаллографии – так называется наука о строении и свойствах кристаллов – русским учёным Евграфом Степановичем Фёдоровым.
Слайд 12Евграф Степанович Фёдоров (1853— 1919) — русский кристаллограф, минералог и математик. Крупнейшее достижение
Евграф Степанович Фёдоров (1853— 1919) — русский кристаллограф, минералог и математик. Крупнейшее достижение

Страстная, протестующая против насилия и несправедливости натура Е. С. Фёдорова приводит его в партию "Земля и Воля"; членом её он становится ещё в 1876 г. в бытность свою студентом Технологического института. Е. С. Фёдоров принял активное участие в подпольной работе. В 1877 году он по заданию партии, с целью установления связи с заграничными революционными организациями, объезжает
францию, Бельгию и Германию, зарабатывая средства для жизни тяжёлым физическим трудом. В Германии он знакомится с В. Либкнехтом и А. Бебелем и под их влиянием проникается социал-демократическими идеями. Он принимает участие в немецком рабочем движении, работает наборщиком социал-демократической газеты.
Слайд 13Е.С. Фёдоров не только указал на возможность определения вещества по форме кристалла,
Е.С. Фёдоров не только указал на возможность определения вещества по форме кристалла,

Для анализа вещества методом Е.С. Фёдорова требуется иметь маленький кристаллик, размером хоть с песчинку. У этого кристаллика мы измеряем на специальных приборах – гониометрах – углы между гранями. Затем, пользуясь правилами, разработанными Фёдоровым, мы определяем, к какой группе веществ принадлежит исследуемый кристалл, и по совпадению данных измерения с цифрами, приведёнными в «Царстве кристаллов», находим, с каким веществом мы имеем дело. Разумеется, анализ не может быть проведён в том случае, если данное вещество никогда не изучалось и сведений о нём нет в книге.
Анализ методом Е.С. Фёдорова оказал уже не мало услуг промышленности. Например, в 1938 году с помощью определителя кристаллов было обнаружено присутствие в россыпях на Урале важнейшей оловянной руды – касситерита, кристаллы которого были ранее ошибочно отнесены к другому минералу – рутилу (окись титана).
Слайд 14Симметрия
На рисунке правая часть скульптуры в точности совпадёт с отражением левой её
Симметрия
На рисунке правая часть скульптуры в точности совпадёт с отражением левой её
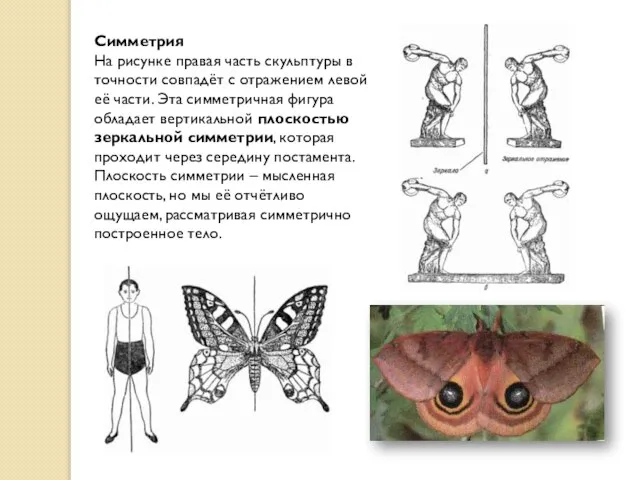
Слайд 15На рисунке изображена детская бумажная вертушка. Она тоже симметрична, но плоскость симметрии
На рисунке изображена детская бумажная вертушка. Она тоже симметрична, но плоскость симметрии
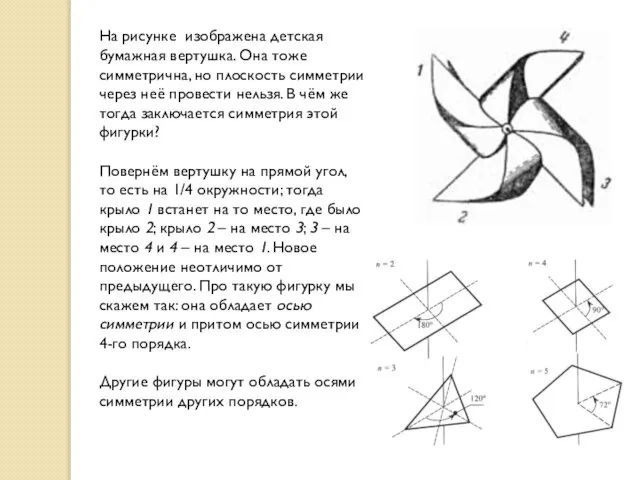
Повернём вертушку на прямой угол, то есть на 1/4 окружности; тогда крыло 1 встанет на то место, где было крыло 2; крыло 2 – на место 3; 3 – на место 4 и 4 – на место 1. Новое положение неотличимо от предыдущего. Про такую фигурку мы скажем так: она обладает осью симметрии и притом осью симметрии 4-го порядка.
Другие фигуры могут обладать осями симметрии других порядков.
Слайд 16Фигура обладает симметрией, если существует движение (преобразование не тождественное), переводящее ее в
Фигура обладает симметрией, если существует движение (преобразование не тождественное), переводящее ее в

К фундаментальным понятиям симметрии относятся плоскость симметрии, ось симметрии, центр симметрии. Можно также рассматривать трансляционную симметрию.
Плоскостью симметрии P называется такая плоскость, которая делит фигуру на две зеркально равные части, расположенные друг относительно друга так, как предмет и его зеркальное отражение. Например, изображенный на рис. слева равнобедренный треугольник ABC высотой BD разделяется на две зеркально равные половины ABD и BCD; при этом высота BD является "следом" плоскости симметрии P, перпендикулярной плоскости треугольника. На рис.справа изображен также прямоугольный параллелепипед (кирпичик, спичечный коробок), который имеет три взаимно перпендикулярные плоскости симметрии 3P. Нетрудно установить, что куб обладает девятью плоскостями симметрии - 9P.
Слайд 17Осью симметрии L называется такая прямая линия, вокруг которой симметричная фигура может
Осью симметрии L называется такая прямая линия, вокруг которой симметричная фигура может
Слайд 18Наконец, центром симметрии C называется такая особая точка внутри фигуры, характеризующаяся тем,
Наконец, центром симметрии C называется такая особая точка внутри фигуры, характеризующаяся тем,
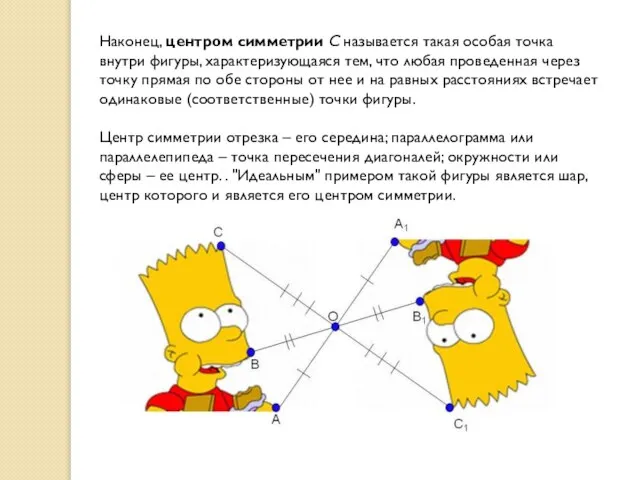
Центр симметрии отрезка – его середина; параллелограмма или параллелепипеда – точка пересечения диагоналей; окружности или сферы – ее центр. . "Идеальным" примером такой фигуры является шар, центр которого и является его центром симметрии.
Слайд 19Чтобы понять, что такое трансляционная симметрия, нам придётся поговорить… об обоях. Посмотрите
Чтобы понять, что такое трансляционная симметрия, нам придётся поговорить… об обоях. Посмотрите

Трансляционная симметрия — тип симметрии, при которой свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Трансляционная симметрия свойственна для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число.
Слайд 20Симметрия широко встречается в объектах живой и неживой природы. Например, симметрия в
Симметрия широко встречается в объектах живой и неживой природы. Например, симметрия в

Понятие "симметрии" является центральным при исследовании кристаллов. При этом симметрия внешних форм кристаллов определяется симметрией его атомного строения, которая обуславливает и симметрию физических свойств кристалла.
Особенно широко понятие "симметрии" применительно к физическим законам используется в современной физике. Если законы, устанавливающие соотношения между величинами или определяющие изменение этих величин со временем, не меняются при определенных операциях (преобразованиях), которым может быть подвергнута система, то говорят, что эти законы обладают симметрией (или инвариантны) относительно данных преобразований.
Например, закон тяготения действует в любой точки пространства, то есть он является инвариантным по отношению переноса системы как целого в пространстве.
Слайд 21Какое же отношение имеют обои к кристаллу?
Каждое тело, в том числе и
Какое же отношение имеют обои к кристаллу?
Каждое тело, в том числе и

Кристалл представляет собой «пространственные обои». Пространственные, то есть объёмные, а не плоские элементарные ячейки – это «кирпичи», прикладыванием которых друг к другу в пространстве строится кристалл.
Слайд 22Структура кристалла – это пространственное расположение его атомов (или молекул). Если с
Структура кристалла – это пространственное расположение его атомов (или молекул). Если с

Сколько же способов построения «пространственных обоев» из элементарных кусков? Эта сложная математическая задача была также решена Е.С. Фёдоровым. Он доказал, что должны существовать 230 способов построения кристалла или, как сейчас говорим, 230 фёдоровских групп. Открытие Е.С. Фёдорова принадлежит к величайшим достижениям русской науки. Начатые примерно через 20 лет после вывода Фёдорова опытные проверки его теории – они стали возможными лишь после открытия рентгеновского структурного анализа – привели к блестящему её подтверждению. Не было найдено ни одного кристалла, который не принадлежал бы к той или иной фёдоровской группе.
Слайд 23Существуют простые кристаллы, построенные из атомов одного сорта. Например, алмаз – это
Существуют простые кристаллы, построенные из атомов одного сорта. Например, алмаз – это

Однако в кристалле всегда можно выделить наименьшую повторяющуюся группу атомов (в простейшем случае это будет один атом), что соответствует повторяющейся на плоских обоях рисунка одной фигурке.
В кристалле всегда можно найти элементарную ячейку, – то есть такой параллелепипед (для плоских обоев это был прямой или косоугольный параллелограмм), последовательным перемещением которого параллельно самому себе на расстояния, равные его рёбрам, можно воспроизвести весь кристалл.
Вершины ячейки кристаллографы называют узлами. Обычно их удобнее всего размещать в центрах атомов кристалла
Если изобразить в пространстве строение кристалла, отмечая только узлы и соединяющие их линии, то возникнет своего рода «скелет» кристалла. Такое изображение кристалла называется кристаллической решёткой.
Слайд 24Основная особенность кристаллической структуры заключается в её повторяемости через строго одинаковые расстояния.
Основная особенность кристаллической структуры заключается в её повторяемости через строго одинаковые расстояния.
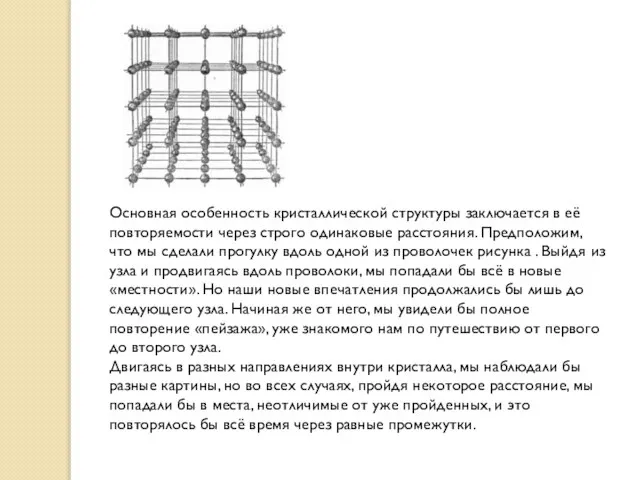
Двигаясь в разных направлениях внутри кристалла, мы наблюдали бы разные картины, но во всех случаях, пройдя некоторое расстояние, мы попадали бы в места, неотличимые от уже пройденных, и это повторялось бы всё время через равные промежутки.
Слайд 25Гранецентрированная
Объёмно-центрированная
Базо-центрированная
Примитивная
Решетка Браве является математической моделью, отражающей трансляционную симметрию кристалла. Все многообразие кристаллов
Гранецентрированная
Объёмно-центрированная
Базо-центрированная
Примитивная
Решетка Браве является математической моделью, отражающей трансляционную симметрию кристалла. Все многообразие кристаллов
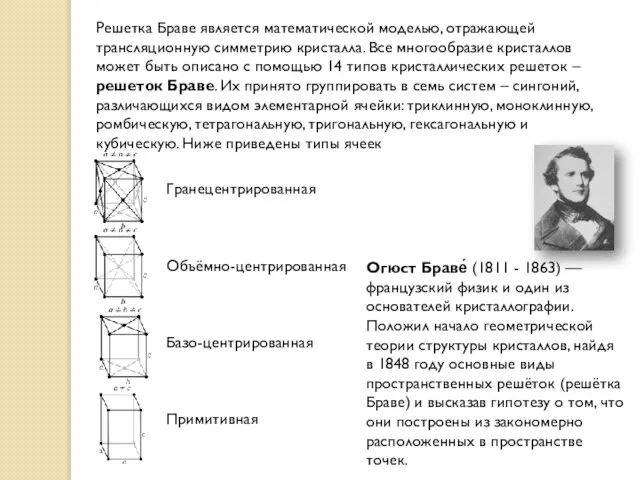
Огюст Браве́ (1811 - 1863) — французский физик и один из основателей кристаллографии.
Положил начало геометрической теории структуры кристаллов, найдя в 1848 году основные виды пространственных решёток (решётка Браве) и высказав гипотезу о том, что они построены из закономерно расположенных в пространстве точек.
Слайд 26Решетка Браве является математической моделью, отражающей трансляционную симметрию кристалла. В общем случае,
Решетка Браве является математической моделью, отражающей трансляционную симметрию кристалла. В общем случае,

Понятие решётки Браве связано с основными трансляционными векторами. Основным трансляционным вектором называется минимальный в данном направлении вектор перехода из данной точки в ближайшую эквивалентную.
Задав нулевую точку, строим совокупность точек по правилу:
Где n1, n2, n3 -произвольные целые числа.
Получившаяся решётка - решётка Браве.
Слайд 27В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на ряд кристаллических
В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на ряд кристаллических

триклинная сингония — наименьшая симметрия, нет одинаковых углов, нет осей одинаковой длины;
моноклинная сингония — два прямых угла, нет осей одинаковой длины
Слайд 28ромбическая сингония — три прямых угла нет осей одинаковой длины;
гексагональная сингония — две оси
ромбическая сингония — три прямых угла нет осей одинаковой длины;
гексагональная сингония — две оси
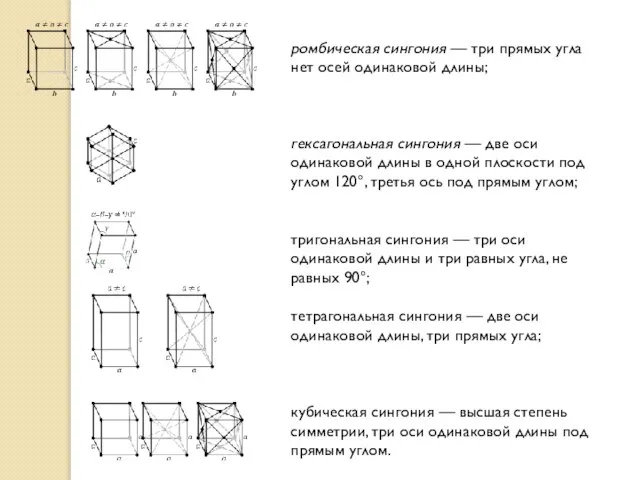
тригональная сингония — три оси одинаковой длины и три равных угла, не равных 90°;
тетрагональная сингония — две оси одинаковой длины, три прямых угла;
кубическая сингония — высшая степень симметрии, три оси одинаковой длины под прямым углом.
Слайд 29Сэр Уильям Генри Брэгг( 1862-1942) — английский физик, лауреат Нобелевской премии по физике
Сэр Уильям Генри Брэгг( 1862-1942) — английский физик, лауреат Нобелевской премии по физике

Сэр Уильям Лоренс Брэгг OBE (1890 — 1971) — австралийский физик, лауреат Нобелевской премии по физике за 1915 год (совместно со своим отцом Уильямом Генри Брэггом). Самый молодой нобелевский лауреат по физике за всю историю премии.
Гео́ргий (Ю́рий) Ви́кторович Вульф (1863 — 1925) — советский кристаллограф, член-корреспондент РАН (1921).
Слайд 30Толкование рентгеновской дифракционной картины, полученной в опыте Лауэ, оказалось довольно сложным, и
Толкование рентгеновской дифракционной картины, полученной в опыте Лауэ, оказалось довольно сложным, и
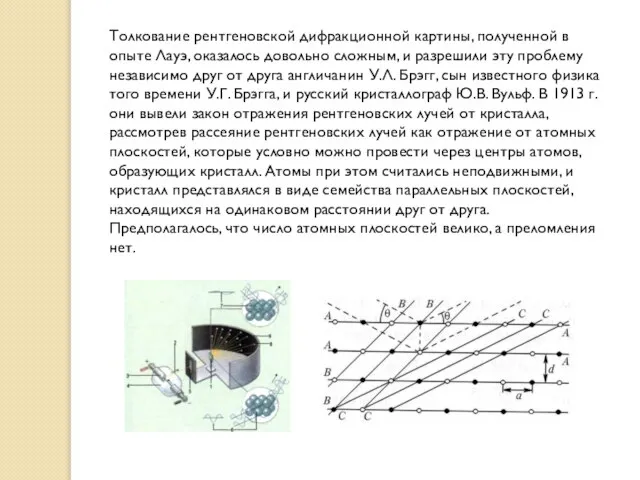
Слайд 31Простейший случай Брэгговской дифракции возникает при рассеянии видимого света на дифракционной решётке.
Простейший случай Брэгговской дифракции возникает при рассеянии видимого света на дифракционной решётке.
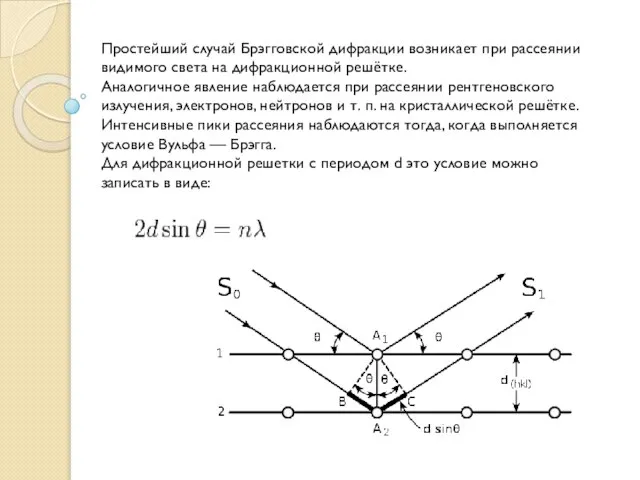
Аналогичное явление наблюдается при рассеянии рентгеновского излучения, электронов, нейтронов и т. п. на кристаллической решётке. Интенсивные пики рассеяния наблюдаются тогда, когда выполняется условие Вульфа — Брэгга.
Для дифракционной решетки с периодом d это условие можно записать в виде:
Слайд 32Важной датой в истории физики твердого тела является 8 июня 1912 года. В

Все современные данные о внутреннем строении кристаллов получены при помощи рентгеновского структурного анализа.Маленький, размером 0,5–1 мм, кристаллик ставится на пути узкого рентгеновского луча. За кристаллом помещается фотопластинка. Наряду с прошедшим сквозь кристалл лучом возникает ряд отклонённых лучей. Явление это носит название дифракции.
Слайд 33Макс фон Лауэ (1879 — 1960) — немецкий физик, лауреат Нобелевской премии по физике
Макс фон Лауэ (1879 — 1960) — немецкий физик, лауреат Нобелевской премии по физике

Метод Лауэ
Немонохроматический пучок рентгеновских лучей (электронов или нейтронов) направляется на неподвижно закрепленный монокристалл . Каждое пятно на лауэграмме соответствует плоскости решетки, ориентация которой полностью определяется направлением дифракционного луча.
( а схема метода Лауэ; б − лауэграмма монокристалла пирита (FeS2))
.
Слайд 34Пе́тер Йо́зеф Вильге́льм Деба́й (1884— 1966) — голландский физик, лауреат Нобелевской премии по
Пе́тер Йо́зеф Вильге́льм Деба́й (1884— 1966) — голландский физик, лауреат Нобелевской премии по

Метод порошка (Дебая)
Пучок монохроматических лучей падает на поликристаллический образец. Падающие лучи отражаются от тех кристаллитов, которые по отношению к направлению падающего пучка оказываются ориентированы так, что выполняется условие Вульфа-Брэггов (а − схема съемки поликристалла в цилиндрической камере; б − рентгенограмма на фотопленке, полученная при съемке в цилиндрической камере )

 Реформирование образования требует развития СИСТЕМЫ ДИСТАНЦИОННОГО ОБУЧЕНИЯ
Реформирование образования требует развития СИСТЕМЫ ДИСТАНЦИОННОГО ОБУЧЕНИЯ ООО Воскресенский центр производства упаковки. Приобретение оборудования для производства импортозамещающей полимерной упаковки
ООО Воскресенский центр производства упаковки. Приобретение оборудования для производства импортозамещающей полимерной упаковки Гипертония
Гипертония Импульс тела
Импульс тела Конфликт и как из него выйти
Конфликт и как из него выйти Обратная перспектива
Обратная перспектива 5кл.повествование
5кл.повествование Я иду в детский сад. Адаптация ребенка к ДОУ
Я иду в детский сад. Адаптация ребенка к ДОУ Презентация на тему ЗВЁЗДЫ И СОЗВЕЗДИЯ
Презентация на тему ЗВЁЗДЫ И СОЗВЕЗДИЯ  20140320_proverochnaya_po_teme_relef_rossii
20140320_proverochnaya_po_teme_relef_rossii Инновационный опыт
Инновационный опыт ОЦЕНКА ПЕРСОНАЛА В КОМПАНИИ
ОЦЕНКА ПЕРСОНАЛА В КОМПАНИИ Живопись. Основные разновидности техники живописи
Живопись. Основные разновидности техники живописи Forces in Magnetic Field
Forces in Magnetic Field  Народные промыслы. Городецкая роспись
Народные промыслы. Городецкая роспись Постановление Правительства Москвы № 86-ПП от 22.03.2011 «О проведении пилотного проекта по развитию общего образования в городе Моск
Постановление Правительства Москвы № 86-ПП от 22.03.2011 «О проведении пилотного проекта по развитию общего образования в городе Моск Ф е р м е н т ы для переработки плодов
Ф е р м е н т ы для переработки плодов Презентация на тему Влияние солнечной активности на процессы, происходящие на Земле
Презентация на тему Влияние солнечной активности на процессы, происходящие на Земле  Презентация на тему Воздух
Презентация на тему Воздух  Electronic Sports League
Electronic Sports League МЕЖДУНАРОДНЫЙ ЦЕНТР ПО ИНФОРМАТИКЕ И ЭЛЕКТРОНИКЕ (ИнтерЭВМ) www.mifp.ru www.inevm.ru Технологии образовательных ресурсовICIE Технологическое
МЕЖДУНАРОДНЫЙ ЦЕНТР ПО ИНФОРМАТИКЕ И ЭЛЕКТРОНИКЕ (ИнтерЭВМ) www.mifp.ru www.inevm.ru Технологии образовательных ресурсовICIE Технологическое  Моя педагогическая философия
Моя педагогическая философия Презентация_Microsoft_PowerPoint
Презентация_Microsoft_PowerPoint Материки и океаны
Материки и океаны Культурно-массовое мероприятие
Культурно-массовое мероприятие «Оценка эффективности деятельности педагогического работника различными участниками образовательного процесса
«Оценка эффективности деятельности педагогического работника различными участниками образовательного процесса Электрические схемы устройств для преобразования электрической энергии на постоянном и переменном токе. (Лекция 10)
Электрические схемы устройств для преобразования электрической энергии на постоянном и переменном токе. (Лекция 10) погребальный обряд на Руси
погребальный обряд на Руси