Содержание
- 2. ФОРМУЛЫ (a + b)²=a²+2ab+b² Квадрат суммы (a - b) ²=a²-2ab+b² Квадрат разности a²-b²=(a - b)(a +
- 3. ПРИМЕРЫ (x + y) 2 (x - y) 2 Квадрат суммы (3x + 2)2 = (Зх)2+
- 4. ПРИМЕРЫ (x + y) 3 (x - y) 3 Куб суммы (2a+ b) 3=2a3+3(2a)2 b+ +3•2a•b
- 5. ПРИМЕРЫ (x 3 +y 3) (x3-y3) Сумма кубов 2x3+3y 3=(2x+3y)(2x2-6xy+3y2); a3+2b3=(a+2b)(a2-2ab+ +2b 2); 123+83=(12+8)·(122-12·8+82)= 20·(144-96+64)= 20·112=
- 6. ПРИМЕРЫ Разность квадратов 4a2-9b2 = (2a-3b)(2a+3b); (7a-6b)(7a+6b)=49a 2-36b2; (Зх - 2у) (Зх + 2у)= (З x)2
- 7. РАЗЛОЖИТЕ НА МНОЖИТЕЛИ 1) x2-25=(x-5)(x+5) 2)16-c2=(4-c)(4+c) 3) a2-6a+9=(a-3) 2 4) x2+8x+16=(x+4) 2 5) a3-8=(a-2)(a2+2a-4) 6) b3+27=(b+3)(b2-3b+9)
- 8. ПРИМЕРЫ 1) 3(2x-1)2+5(3-x)2 =3(4x2-4x+1)+5(9-6x+x2)= =12x2-12x+3+45-30x+5x2=17x2-42x+48 2) 2(4x-1)2 -4(1-2x)2=2(16x2-8x+1)-4(1- -4x+4x2)=32x 2 -16x+2-4+16x-16x2=16x2-2 3) 7(1-x)(1+x)=7(1-x2)=7-7x2 4)(3b-2a)(3b+2a)+(2a-2b)2=9b2-4a2+4a2- -8ab+4b2=9b2-8ab+4b2 5)(2+2x)³=2³+3·4·2x+3·2·4x2+8x³=8+24x+
- 9. УРАВНЕНИЯ a) 8x(1+2x)(4x+3)(4x-3)=2x 8x+16x²-16x²-9=2x 8x-9=2x 6x=-9 x=-1.5 Ответ:-1.5 б)(x -6)²-x(x+8)=2 x2-12x+36-x2-8x=2 -20x=2-36 -20x=-34 x=1.7 Ответ: 1.7
- 10. УРАВНЕНИЯ (x-4x)(x+4x)+(3x-4)(x+2)=(2x+3)2 x2-16+3x2+6x-4x-8=4x2+12x+9 -10x=33 x=-3.3 Ответ:3.3 x(x-1)-(x-5)2=2 x2-x-(x2-10x+25)=2 x2-x-x2+10x-25=2 9x=27 x=3 Ответ: 3 ( 2x+3)2-4(x-1)(x+1)=49 4x2+12x+9-4(x2-1)=49
- 12. Скачать презентацию





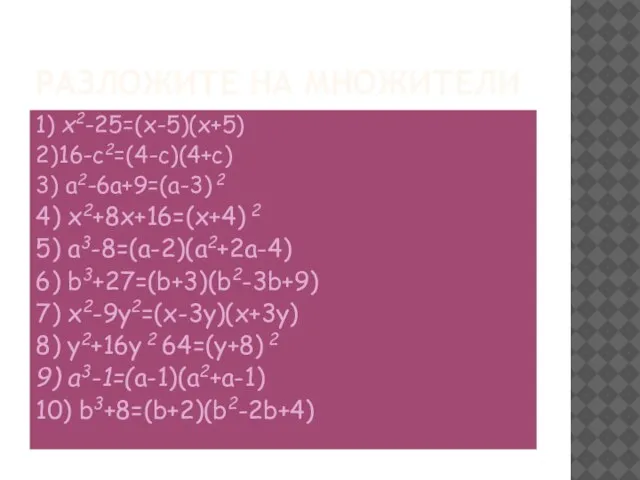



 Банкротство гражданина и его законодательное регулирование
Банкротство гражданина и его законодательное регулирование Основы теории государства и права. Лекция 1
Основы теории государства и права. Лекция 1 Первый властелин единого Китая
Первый властелин единого Китая Примеры недостоверной информации в составе заявок
Примеры недостоверной информации в составе заявок Help user regain control over their phone
Help user regain control over their phone Виды изобразительного искусства и основы их образного языка
Виды изобразительного искусства и основы их образного языка Риторика. Ошибки, касающиеся аргументов
Риторика. Ошибки, касающиеся аргументов Создание электронного учебника
Создание электронного учебника Методическая работа школы
Методическая работа школы Центр языковых переводов «GMC Translation Service» – это международная компания с 15-летним опытом работы в сфере языковых переводов. Сегодня
Центр языковых переводов «GMC Translation Service» – это международная компания с 15-летним опытом работы в сфере языковых переводов. Сегодня Блез Паскаль
Блез Паскаль Виртуальная галерея иллюзий
Виртуальная галерея иллюзий Террористы-смертники. Южанина, Митрофанов
Террористы-смертники. Южанина, Митрофанов СОВРЕМЕННЫЕ ИНФРАСТРУКТУРНЫЕ ТЕХНОЛОГИИ ОРГАНИЗАЦИИ ЭЛЕКТРОННОГО ДОКУМЕНТООБОРОТА НА ФИНАНСОВОМ РЫНКЕ
СОВРЕМЕННЫЕ ИНФРАСТРУКТУРНЫЕ ТЕХНОЛОГИИ ОРГАНИЗАЦИИ ЭЛЕКТРОННОГО ДОКУМЕНТООБОРОТА НА ФИНАНСОВОМ РЫНКЕ Инструментальная теория подбора супругов Р. Сентерсон
Инструментальная теория подбора супругов Р. Сентерсон Простые истины воспитания здорового малыша
Простые истины воспитания здорового малыша Topic London
Topic London Пищеварение в ротовой полости
Пищеварение в ротовой полости Системный подход на благо людей и природы
Системный подход на благо людей и природы Международное гуманитарное право в период вооруженных конфликтов
Международное гуманитарное право в период вооруженных конфликтов Зарубежная Азия – крупнейший регион мира
Зарубежная Азия – крупнейший регион мира Формирование психологически совместимых трудовых коллективов. Тема 9
Формирование психологически совместимых трудовых коллективов. Тема 9 Тарарушки из села Полховский Майдан. Мотивы росписи (часть 2)
Тарарушки из села Полховский Майдан. Мотивы росписи (часть 2) интеллектуальный марафон
интеллектуальный марафон Элементы формообразования
Элементы формообразования Определение в русском языке (8 класс)
Определение в русском языке (8 класс) Орнаменты и принты
Орнаменты и принты Организационные структуры управления
Организационные структуры управления