Содержание
- 2. План 1. Основные понятия теории геометрических построений: сущность геометрических построений; основные инструменты построений и их аксиомы;
- 3. Сущность геометрических построений Геометрические построения – раздел геометрии, изучающий вопросы и методы построения геометрических фигур с
- 4. Структура задачи на построение Условия – заданные элементы искомой фигуры или совокупности фигур и их характеристики.
- 5. Инструменты построений Классические математическая линейка; циркуль. Дополнительные чертежный треугольник ; транспортир. Чертежные машины пантограф; эллипсограф; рейсмус;
- 6. Аксиомы инструментов Линейка: Л1: построить отрезок, соединяющий две данные (построенные) точки. Л2: построить прямую, проходящую через
- 7. Аксиомы инструментов Циркуль: Ц1: построить окружность, если даны ее центр и отрезок, равный радиусу. Ц2: построить
- 8. Простейшие задачи на построения (постулаты построения) П1: Построить (провести) на плоскости произвольную прямую. П2: Построить (провести)
- 9. Сущность задачи на построение Состоит в построении заданной геометрической фигуры с помощью данных чертежных инструментов (как
- 10. Этапы решения задач на построение Анализ – осуществление поиска решения задачи классическими методами восходящего анализа, составление
- 11. В школьной практике практически никогда эти четыре этапа не реализуются. При решении первых задач на построение
- 12. Методы геометрических построений Суть любого из методов геометрических построений – построение в конечном счете отдельных точек,
- 13. Метод пересечений Метод ГМТ – геометрического места точки – основной метод. ГМТ – множество точек пространства
- 14. Суть метода пересечений Пусть нужно построить точку Х, удовлетворяющую двум данным условиям, и F1 и F2
- 15. Метод преобразований (подобия, симметрии, параллельного переноса и т.п.) Суть метода: Первоначально вместо искомой фигуры строится вспомогательная
- 16. Координатный метод Суть: построение точки через определение ее положения на плоскости с помощью чисел (координат) или
- 17. Алгебраический метод Суть: использование соотношений между простейшими фигурами как элементами более сложных фигур. Например: построение отрезка,
- 18. Метод оригами Метод оригами - практический метод, основанный на перегибании (реальном или мысленном). Возможности перегибания листа
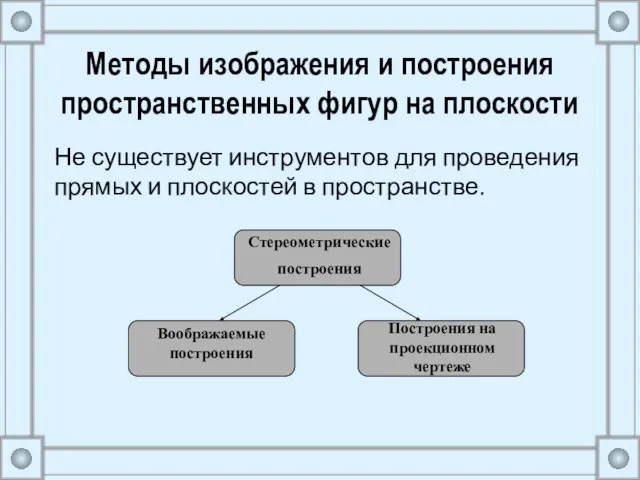
- 19. Методы изображения и построения пространственных фигур на плоскости Не существует инструментов для проведения прямых и плоскостей
- 20. Воображаемые построения Воображаемые построения – рисунки или изображения, назначение которых – создать наглядное представление о происходящем
- 21. Построение по проекционным чертежам Изображенной в стереометрии считают любую фигуру, подобную параллельной проекции данной фигуры на
- 22. Цель изучения геометрических построений Познавательный аспект усвоение основных видов и методов геометрических построений; применение различных способов
- 23. I уровень Знания – ученик знает: термины и алгоритмы решения основных задач на построение; правила использования
- 24. II уровень Знания – ученик знает этапы решения задач на построения; приемы выполнения действий, характерных каждому
- 25. III уровень Знание – ученик знает методы геометрических построений и их логическую основу; связь методов построений
- 26. Развивающий аспект Создание условий для развития: познавательного интереса; речи и умения учиться; логического мышления и пространственного
- 27. Воспитательный аспект Включает в себя воспитание: интереса к математике; аккуратности, точности; эстетического восприятия; сообразительности; инициативы; культуры
- 28. Технологическая схема методов построения Изучение теории, на которой основан метод. Рассмотрение с помощью учителя примеров задач,
- 30. Скачать презентацию


























 Поколение молодости REV 7-2014
Поколение молодости REV 7-2014 Взаимодействие агентов в многоагентных системах
Взаимодействие агентов в многоагентных системах ФАКТОГРАФИЧЕСКИЕ БАЗЫ ДАННЫХ НАЦИОНАЛЬНОЙ БИБЛИОТЕКИ БЕЛАРУСИ КАК ИСТОЧНИК ИНФОРМАЦИИ О НАЦИОНАЛЬНЫХ ОБЪЕКТАХ Кузьминич Т. Нац
ФАКТОГРАФИЧЕСКИЕ БАЗЫ ДАННЫХ НАЦИОНАЛЬНОЙ БИБЛИОТЕКИ БЕЛАРУСИ КАК ИСТОЧНИК ИНФОРМАЦИИ О НАЦИОНАЛЬНЫХ ОБЪЕКТАХ Кузьминич Т. Нац Филиппова Елена Константиновна – учитель Филиппова Елена Константиновна – учитель русского языка и литературы Квалификационная
Филиппова Елена Константиновна – учитель Филиппова Елена Константиновна – учитель русского языка и литературы Квалификационная Новости недели. Новосибирск
Новости недели. Новосибирск Художники Сенгилеевского района
Художники Сенгилеевского района ПрезентацияРаздел 2.2
ПрезентацияРаздел 2.2 Международные модели управления персоналом
Международные модели управления персоналом Цели внедрения системы бюджетирования
Цели внедрения системы бюджетирования Деление плоскости на четыре части, в зарисовке
Деление плоскости на четыре части, в зарисовке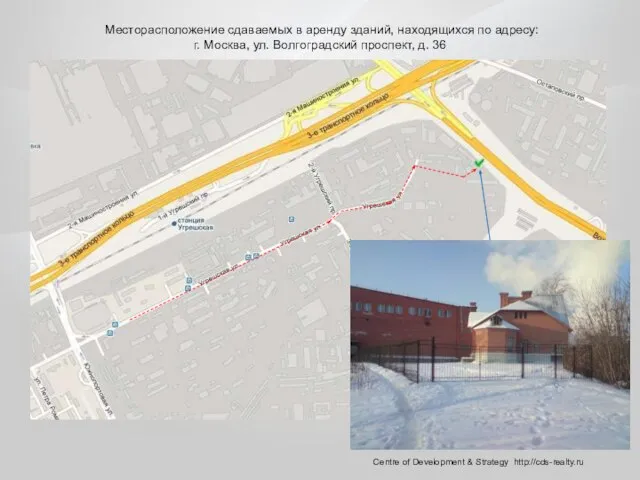 Месторасположение сдаваемых в аренду зданий, находящихся по адресу: г. Москва, ул. Волгоградский проспект, д. 36
Месторасположение сдаваемых в аренду зданий, находящихся по адресу: г. Москва, ул. Волгоградский проспект, д. 36 Филимоновская игрушка. Фотоотчет
Филимоновская игрушка. Фотоотчет Фридрих Шиллер
Фридрих Шиллер Презентация на тему Особые экономические зоны стран мира
Презентация на тему Особые экономические зоны стран мира  Фотоэлектрические модули. (Лекция 5)
Фотоэлектрические модули. (Лекция 5) The Victorian Era 1837 -1901
The Victorian Era 1837 -1901 Династический кризис 1825 г. Выступление декабристов
Династический кризис 1825 г. Выступление декабристов ВЕЛИКАЯ ОТЕЧЕСТВЕННАЯ ВОЙНА СОВЕТСКОГО СОЮЗА.
ВЕЛИКАЯ ОТЕЧЕСТВЕННАЯ ВОЙНА СОВЕТСКОГО СОЮЗА. Электронное взаимодействие между организациями ислужбой занятости населения
Электронное взаимодействие между организациями ислужбой занятости населения Порядок подачи заявления о преступлении
Порядок подачи заявления о преступлении Избушка
Избушка Сказочный мир Шарля Перро
Сказочный мир Шарля Перро ПОП-АРТ
ПОП-АРТ Осенние поделки
Осенние поделки Управление эмоциями
Управление эмоциями КОТЕЛЬНАЯ 4 Х 15 МВт
КОТЕЛЬНАЯ 4 Х 15 МВт Основные этапы разработки ООП
Основные этапы разработки ООП «Свирель серебряного века»
«Свирель серебряного века»