Содержание
- 2. Для представления вещественных чисел (конечных и бесконечных десятичных дробей) используют формат с плавающей точкой (запятой). Форма
- 3. Например, число 35,324 можно записать в таком виде: 0.35324х102 Здесь m=0.35324 — мантисса, n=2 — порядок
- 4. Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ
- 5. Мантисса в нормализованном представлении должна удовлетворять условию: 0,1p ≤ m Иначе говоря, мантисса меньше единицы и
- 6. Машинный порядок Пусть в памяти компьютера вещественное число представляется в форме с плавающей точкой в двоичной
- 7. Машинный порядок В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс,
- 8. Что такое машинный порядок? В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до
- 9. В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие: Если обозначить
- 10. Итак, машинный порядок смещён относительно математического на 64 единицы и имеет только положительные значения. При выполнении
- 11. Теперь мы можем записать внутреннее представление числа 35,324 в форме с плавающей точкой 1) Переведем его
- 12. 2) Запишем в форме нормализованного двоичного числа с плавающей точкой: 0,100011010100101111000110*10110 Здесь мантисса, основание системы счисления
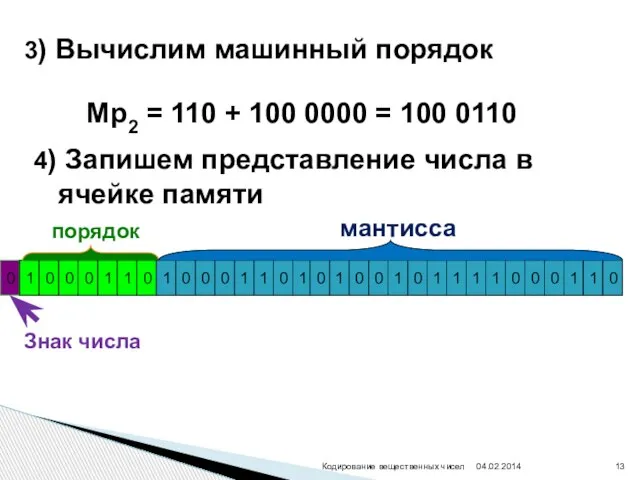
- 13. 3) Вычислим машинный порядок Мр2 = 110 + 100 0000 = 100 0110 4) Запишем представление
- 14. Число в форме с плавающей точкой занимает в памяти компьютера 4 байта (число обычной точности) или
- 15. Для того, чтобы получить внутреннее представление отрицательного числа -35,324, достаточно в полученном выше коде заменить в
- 16. Представьте двоичное число -100,12 в четырёхбайтовом формате. Представьте число сначала в форме с плавающей запятой. Задание:
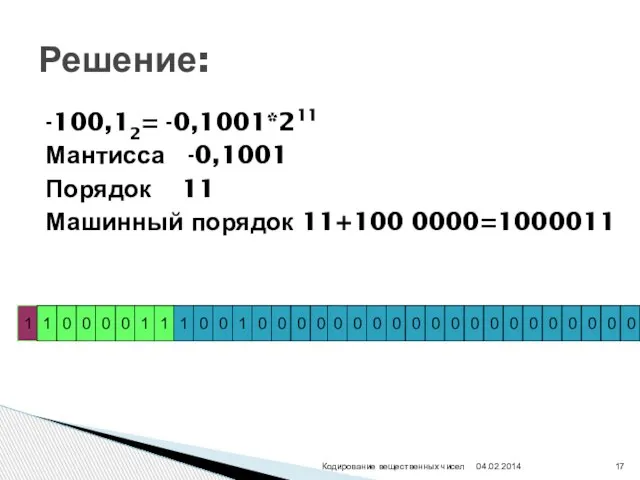
- 17. -100,12= -0,1001*211 Мантисса -0,1001 Порядок 11 Машинный порядок 11+100 0000=1000011 Решение: Кодирование вещественных чисел
- 19. Скачать презентацию














 По повести А.М.Горького «Детство»
По повести А.М.Горького «Детство» 65 лет Великой Победе
65 лет Великой Победе Манипуляция и способы противостоять
Манипуляция и способы противостоять Игра по глава Бэла, Тамань, Фаталист произведения Герой нашего времени Лермонтова
Игра по глава Бэла, Тамань, Фаталист произведения Герой нашего времени Лермонтова  Угольная прокуратура
Угольная прокуратура Калибровка длины и диаметра
Калибровка длины и диаметра Prakticheskaya_rabota_1
Prakticheskaya_rabota_1 Особенности ведения деловых переговоров с японцами
Особенности ведения деловых переговоров с японцами Комбинационные логические схемы
Комбинационные логические схемы Презентация на тему Максим Горький
Презентация на тему Максим Горький  Биометрические технологии в криминалистике
Биометрические технологии в криминалистике Asebmblersko programiranje i procesor i8086
Asebmblersko programiranje i procesor i8086 Как продвигать финансовые услуги аудитории интернет-магазина
Как продвигать финансовые услуги аудитории интернет-магазина Болезни, передаваемые половым путем
Болезни, передаваемые половым путем О и а на конце наречий
О и а на конце наречий Презентация на тему Относительные прилагательные
Презентация на тему Относительные прилагательные  ЛЬГОТНОЕ ЛЕКАРСТВЕННОЕ ОБЕСПЕЧЕНИЕ В РОССИИ: системные противоречия и расходование бюджетных средств на меди
ЛЬГОТНОЕ ЛЕКАРСТВЕННОЕ ОБЕСПЕЧЕНИЕ В РОССИИ: системные противоречия и расходование бюджетных средств на меди Хлеб - всему голова и сила
Хлеб - всему голова и сила ОСНОВНЫЕ ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ
ОСНОВНЫЕ ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ Ощущения. Восприятие. Социальное восприятие. Эффекты социального восприятия
Ощущения. Восприятие. Социальное восприятие. Эффекты социального восприятия Наречие 4 класс
Наречие 4 класс Проект www.ram-torg.ru Торговый Интернет-Центр
Проект www.ram-torg.ru Торговый Интернет-Центр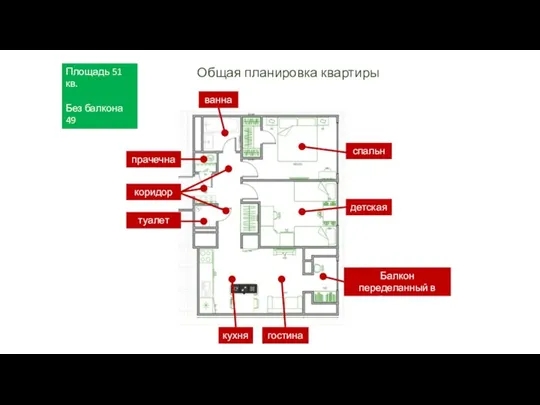 Примерный план ремонта
Примерный план ремонта Классный час «Поговорим о доброте»
Классный час «Поговорим о доброте» Конкуренция и монополия
Конкуренция и монополия  20141019_proektno-issl._deyat-t
20141019_proektno-issl._deyat-t Муниципальное общеобразовательное учреждение «Ахматовская средняя общеобразовательная школа» Тема проекта «Быть всегда всем
Муниципальное общеобразовательное учреждение «Ахматовская средняя общеобразовательная школа» Тема проекта «Быть всегда всем  Имбирное печенье. Новогодний рецепт
Имбирное печенье. Новогодний рецепт