Презентация на тему Комбинаторные задачи: перестановки

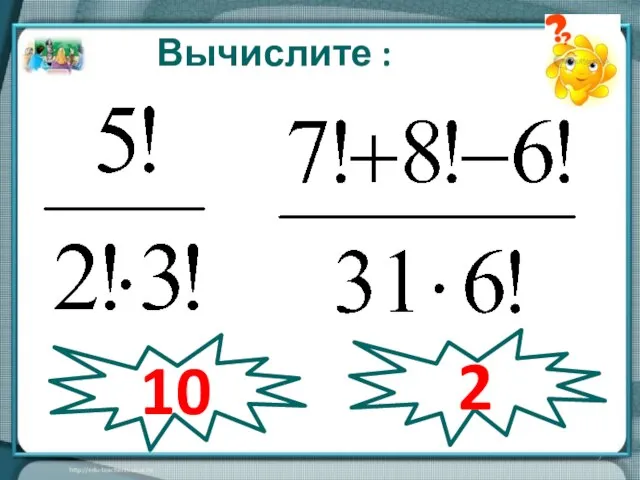
Вычислите :
10
2

Антон, Борис и Виктор купили
3 билета на футбол на 1-е, 2-е, 3-е места первого ряда стадиона. Сколькими способами мальчики могут занять эти места?
Задача:

Решение задачи:
А
А
А
В
Б
Б
Б
В
Может быть такая последовательность:
А может быть и так:
В
В
А
Б
Может быть и так:
В
В
А
А
Б
Б
Ответ: 6 вариантов
Заметим, что 3!=6

Теорема о перестановках элементов конечного множества:
n различных элементов можно расставить
по одному на n различных мест ровно
n! способами.
Перестановкой называется множество из n элементов, записанных в определённом порядке.
Определение:
Рn=n!
Запомните!!!

Вычислите :
56
24

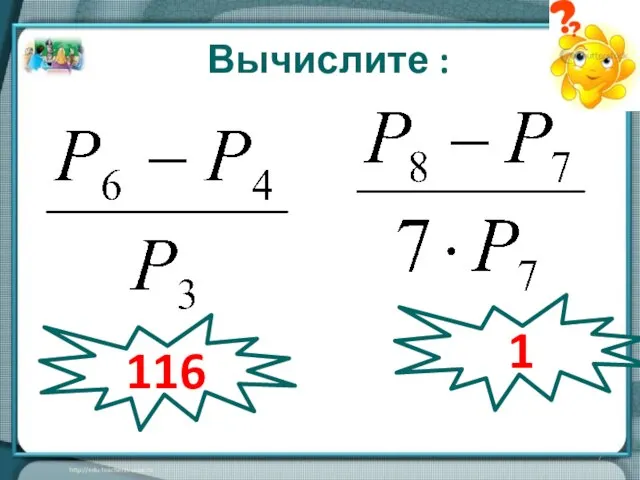
Вычислите :
116
1

2Рх =12
Решите уравнение :
4

Задача:
Пять друзей решили сфотографироваться. Сколькими способами их можно рассадить?
120
Сколько фигурок можно сложить из Танграма?
7!

Найдите количество всех способов, которыми можно составить трехцветный флаг из горизонтальных полос красного, белого и синего цветов.
Задача:
А какие? Чтобы ответить на это вопрос давайте обозначим каждый цвет буквой, с которой
он начинается: К – красный, Б – белый, С – синий.
6

Задача:
Сколько трёхзначных чисел можно получить, используя числа 1,2,3?
Это числа:
123, 132, 213, 231, 312, 321
6
Сколько четырёхзначных чисел можно составить, используя числа 1,2,3,4?
Заметили закономерность?
24

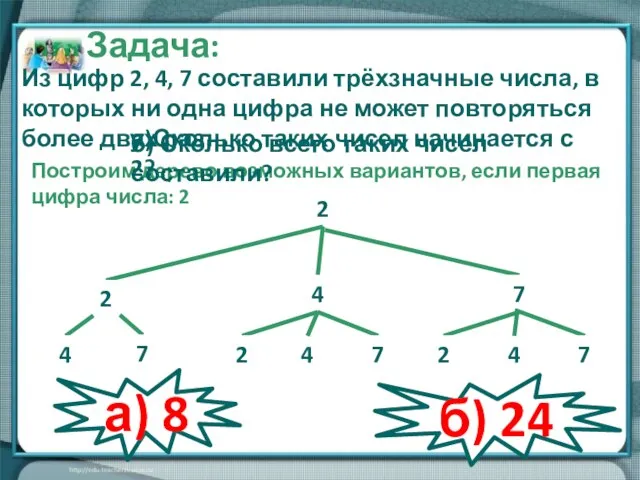
2
4
2
7
4
7
2
7
2
7
4
4
Построим дерево возможных вариантов, если первая цифра числа: 2
Задача:
Из цифр 2, 4, 7 составили трёхзначные числа, в которых ни одна цифра не может повторяться более двух раз.
а) 8
б) 24
б) Сколько всего таких чисел составили?
а)Сколько таких чисел начинается с 2?

247
274
224
227
242
272
244
Задача:
Из цифр 2, 4, 7 составили трёхзначные числа.
2
б)Сколько таких чисел, в которых 2 может повторяться, начинаются с 2?
6
в)Сколько таких чисел, начинаются с двойки и цифра 4 может повторяться?
3
247
274
247
274
а)Сколько таких чисел, в которых ни одна цифра не может повторяться, начинаются с 2?

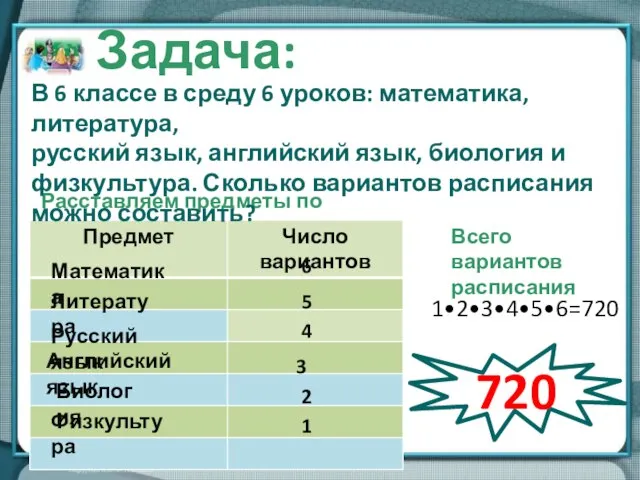
Расставляем предметы по порядку
Математика
6
Литература
5
Русский язык
4
Английский язык
3
Биология
2
1
Физкультура
Всего вариантов
расписания
1•2•3•4•5•6=720
Задача:
В 6 классе в среду 6 уроков: математика, литература,
русский язык, английский язык, биология и физкультура. Сколько вариантов расписания можно составить?
720

В 6 классе во вторник 5 уроков: физкультура, русский язык, литература, обществознание и математика. Сколько можно составить вариантов расписания на день, зная точно, что математика - последний урок?
Ответ: 24 варианта
Ответ: 24 варианта
Задача:
Чем отличается эта задача от предыдущей?
Какой предмет можно не учитывать при составлении расписания?
4!=24

Имеется девять различных книг, четыре
из которых - учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом ?
Задача:
17280

Проказница мартышка, Осел, Козел, Да косолапый мишка затеяли сыграть квартет…Вам знакомо это произведение?
Задача:
4!=24

Р5 = 5!
Задача:
Петя, Вася, Галя, Света и Марина садятся на скамейку. Сколькими способами можно это сделать?
5!=120

Задача:
Сколькими способами Петя, Вася, Галя, Света и Марина могут сесть так, чтобы Галя и Марина были рядом?
2•4!=48

Задача:
Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Петя был в середине?
4!=24

Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Петя и Вася не были рядом?
Задача:
72

Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Света не была второй слева?
Задача:
96

Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Марина не сидела с краю?
Задача:
72

Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Марина не была непосредственно между Галей и Светой?
Задача:
108

Сколькими способами можно переставить буквы в слове «эскиз»?
Задача:
5!=120

Задача:
Сколько слов можно получить, переставляя буквы в слове «переправа»?
Чем отличается эта задача от предыдущей?
Запишем следующую формулу:
где к –сумма повторений различных букв, а к1,к2,… - повторения каждой различной буквы.
Разберём эту формулу на нашем примере:
Буква «п» встречается 2 раза, «е» – 2 раза, «р» – 2 раза, «а» – 2 раза, «в» – 1 раз, значит, к=2+2+2+2+1=9, к1=2,к2=2,к3=2,к4=3,к5=1. Подставим полученные значения в формулу:
22680

Сколько слов можно получить, переставляя буквы в словах: «молоко»? «математика»?
Задача для самостоятельного решения:
120
1680

1. Весной мама покупает ребенку много фруктов. Она купила банан, яблоко, апельсин, лимон, грушу и киви. Найдите число возможных вариантов съедания фруктов.
2. Одиннадцать футболистов строятся перед началом матча. Первым становится капитан, вторым – вратарь, а остальные – случайным образом. Сколько существует способов построения?
3. Сколькими способами можно расставить на полке 10 книг, из которых 4 книги одного автора, а остальные – разных авторов, так, чтобы книги одного автора стояли рядом?
Домашнее задание: