Содержание
- 2. Функция вида y = kx +b, где k и b числа, а x и y переменные,
- 4. Является ли функция, заданная формулой линейной? Если да, то укажите коэффициенты k и b
- 5. Частный случай линейной функции: при b=0 и k≠0, у= kx
- 6. Построить график функции: 1. Формула: у = 2х, k = 2, k>0 2. Таблица: 3. График:
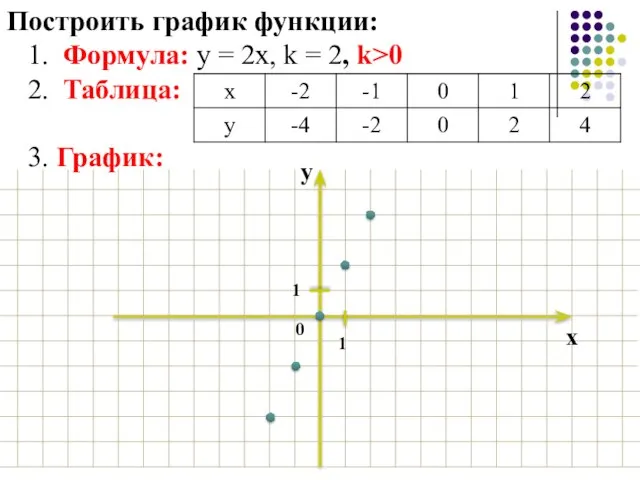
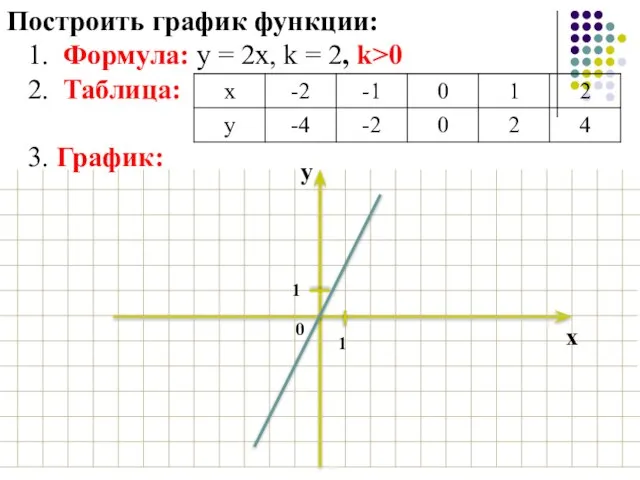
- 7. Построить график функции: 1. Формула: у = 2х, k = 2, k>0 2. Таблица: 3. График:
- 8. Построить график функции: 1. Формула: у = 2х, k = 2, k>0 2. Таблица: 3. График:
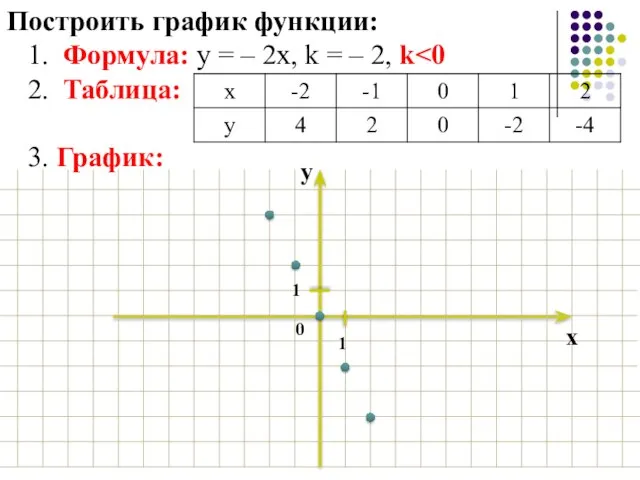
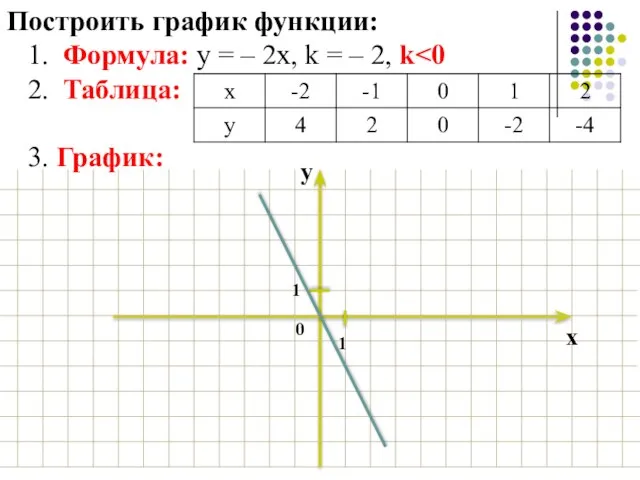
- 9. Построить график функции: 1. Формула: у = – 2х, k = – 2, k 2. Таблица:
- 10. Построить график функции: 1. Формула: у = – 2х, k = – 2, k 2. Таблица:
- 11. Построить график функции: 1. Формула: у = – 2х, k = – 2, k 2. Таблица:
- 12. Через две точки можно провести только одну прямую линию Для построения графика линейной функции достаточно двух
- 13. Выводы: 1) График прямой пропорциональности является прямой, проходящей через начало координат. 2) Если коэффициент пропорциональности k
- 14. Построение графика Графиком функции y=kx является прямая, проходящая через начало координат (0; 0)
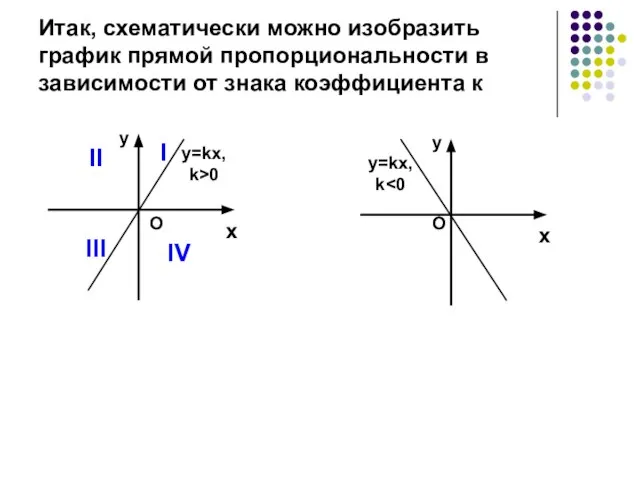
- 15. Итак, схематически можно изобразить график прямой пропорциональности в зависимости от знака коэффициента к I II III
- 17. Скачать презентацию









 Гончарова Ирина Алексеевна
Гончарова Ирина Алексеевна Презентация на тему Палладий
Презентация на тему Палладий Теория фильтров А. Керкгоффа и К. Дэвиса
Теория фильтров А. Керкгоффа и К. Дэвиса Презентация на тему Ремёсла восточных славян
Презентация на тему Ремёсла восточных славян  Исследовательская деятельность в современной школе
Исследовательская деятельность в современной школе Открытка к Дню Победы
Открытка к Дню Победы ПРЕДЕЛЫ МИРОВОГО ЭКОНОМИЧЕСКОГО РОСТА И ПОТРЕБЛЕНИЯ
ПРЕДЕЛЫ МИРОВОГО ЭКОНОМИЧЕСКОГО РОСТА И ПОТРЕБЛЕНИЯ Культура и традиции народов Поволжья
Культура и традиции народов Поволжья Презентация на тему Загрязнение реки Дон
Презентация на тему Загрязнение реки Дон В НАШУ ШКОЛУ ПРИХОДИЛИ МАЛЫШИ!
В НАШУ ШКОЛУ ПРИХОДИЛИ МАЛЫШИ! Написание доклада. (Лекция 7)
Написание доклада. (Лекция 7) Презентация на тему Что такое темперамент
Презентация на тему Что такое темперамент  Автоматизация звука Л
Автоматизация звука Л Ассоциация Правообладателей и Поставщиков контента
Ассоциация Правообладателей и Поставщиков контента ENGLISH TENSES Времена английского глагола Present Simple
ENGLISH TENSES Времена английского глагола Present Simple Эффективная реклама интернет-магазина в системе сравнения цен
Эффективная реклама интернет-магазина в системе сравнения цен здз-ъ
здз-ъ Тепловые двигатели
Тепловые двигатели Презентация (2)
Презентация (2) Глагол
Глагол Художник в театре
Художник в театре Имя М.В.Ломоносова на карте мира
Имя М.В.Ломоносова на карте мира Русская изба. Экскурсия в музей
Русская изба. Экскурсия в музей Профессии типа человек-человек
Профессии типа человек-человек Налог на игорный бизнес
Налог на игорный бизнес Кружок «Юные инспекторы движения» (ЮИД)
Кружок «Юные инспекторы движения» (ЮИД) Наполнение дисплеев Старт
Наполнение дисплеев Старт «Река Руза. Берега бессмертия».
«Река Руза. Берега бессмертия».