Содержание
- 2. Цель: формирование понятия «линейная функция», навыка построения её графика по алгоритму Задачи: Образовательные: - изучить определение
- 3. План урока: I. Организационный момент II. Актуализация опорных знаний III. Изучение новой темы IV. Закрепление: устные
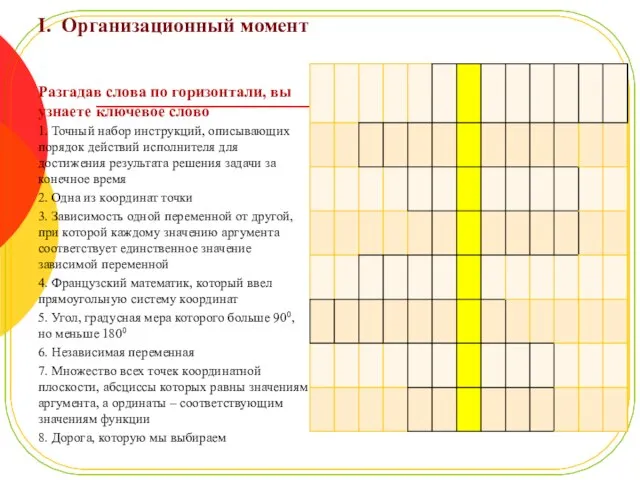
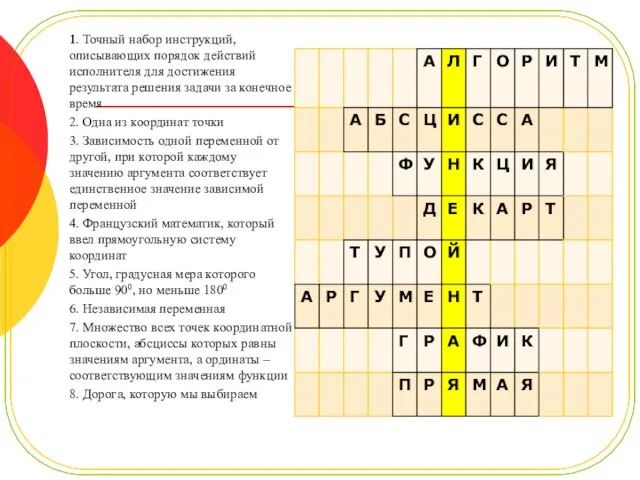
- 4. I. Организационный момент Разгадав слова по горизонтали, вы узнаете ключевое слово 1. Точный набор инструкций, описывающих
- 5. 1. Точный набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное время
- 6. II. Актуализация опорных знаний Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции. Приведем пример.
- 7. III. Изучение новой темы. Уравнение вида y=k x+ m , где k и m – числа
- 8. Алгоритм построения графика линейной функции 1) Составить таблицу для линейной функции (каждому значению независимой переменной поставить
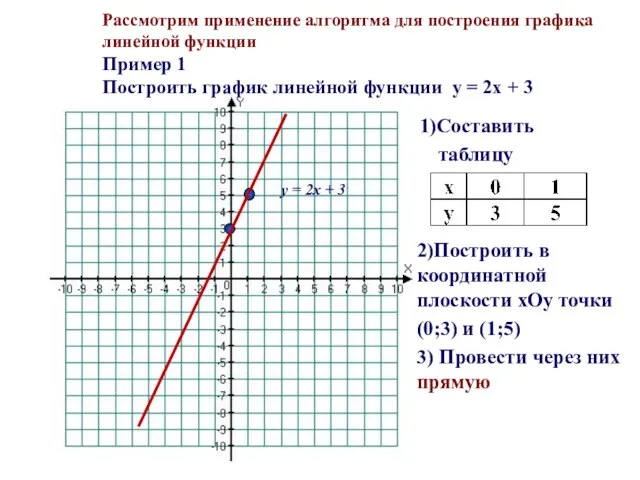
- 9. Рассмотрим применение алгоритма для построения графика линейной функции Пример 1 Построить график линейной функции y =
- 10. Если линейную функцию y=k x+ m рассматривать не при всех значениях x, а лишь для значений
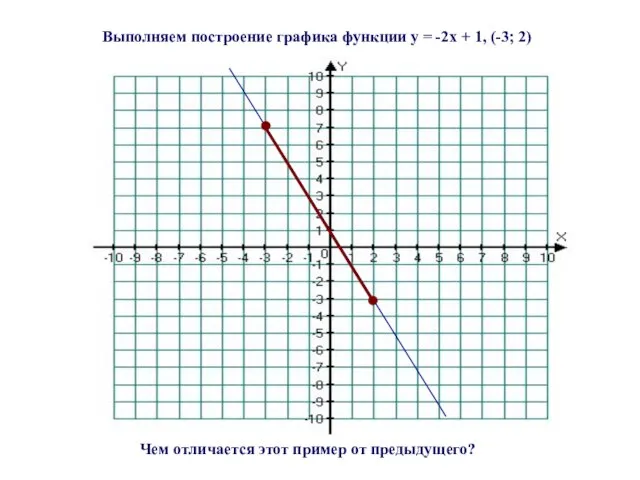
- 11. Рассмотрим следующий пример Пример 2 Построить график линейной функции а) y = -2x + 1, [
- 12. Выполняем построение графика функции y = -2x + 1, [ -3; 2]
- 13. Выполняем построение графика функции y = -2x + 1, (-3; 2) Чем отличается этот пример от
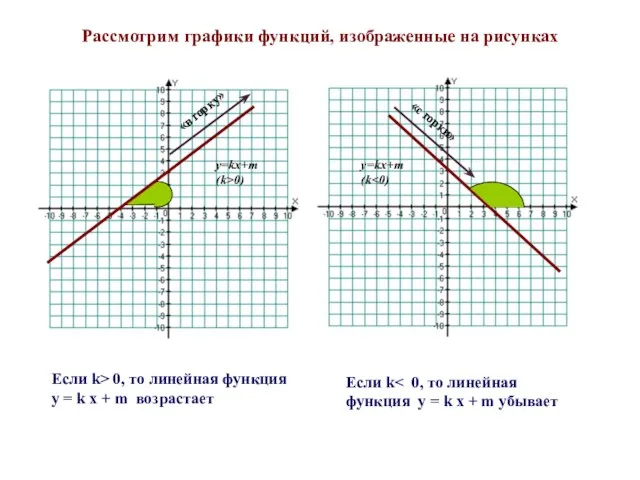
- 14. Рассмотрим графики функций, изображенные на рисунках
- 15. IV. Закрепление изученной темы Выберите, какая функция является линейной функцией
- 16. Подумай
- 17. Молодец
- 18. Выполните следующее задание Линейная функция задана формулой y = -3x – 5. Найдите её значение при
- 19. Проверка решения Если x = 23, то y = -3* 23 – 5=-69 – 5 =
- 20. Найдите значение аргумента, при котором линейная функция y = -2x + 2,4 принимает значение равное 20,4?
- 21. Следующее задание Не выполняя построения ответьте на вопрос: графику какой функции принадлежит А (1;0)?
- 22. Подумай
- 23. Молодец
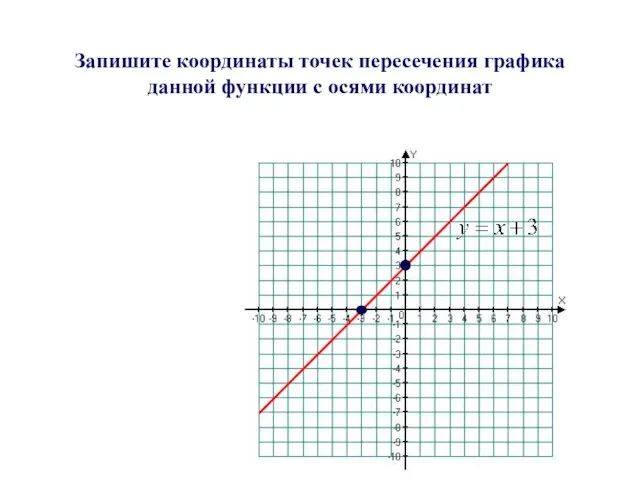
- 24. Запишите координаты точек пересечения графика данной функции с осями координат
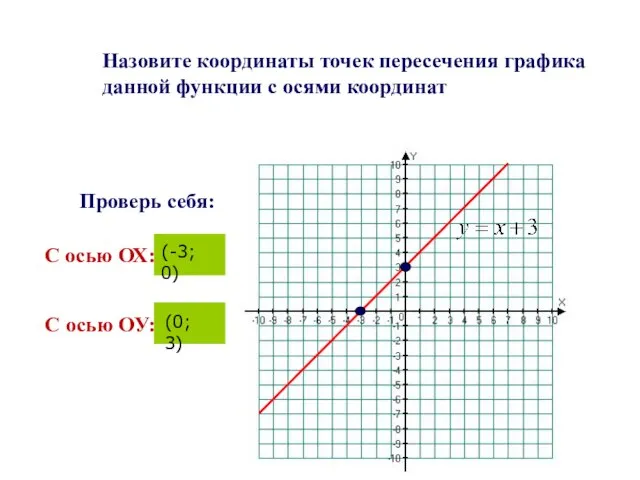
- 25. Назовите координаты точек пересечения графика данной функции с осями координат С осью ОХ: (-3; 0) Проверь
- 26. Физкультурная минутка для глаз
- 27. Постройте график линейной функции построение графика.построение графика.oms
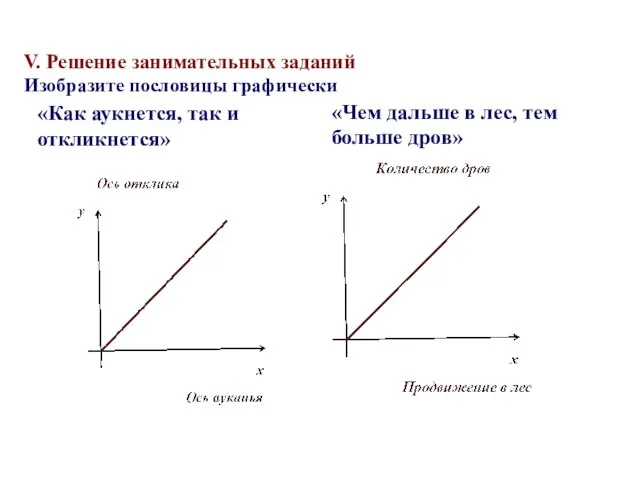
- 28. V. Решение занимательных заданий Изобразите пословицы графически «Как аукнется, так и откликнется» «Чем дальше в лес,
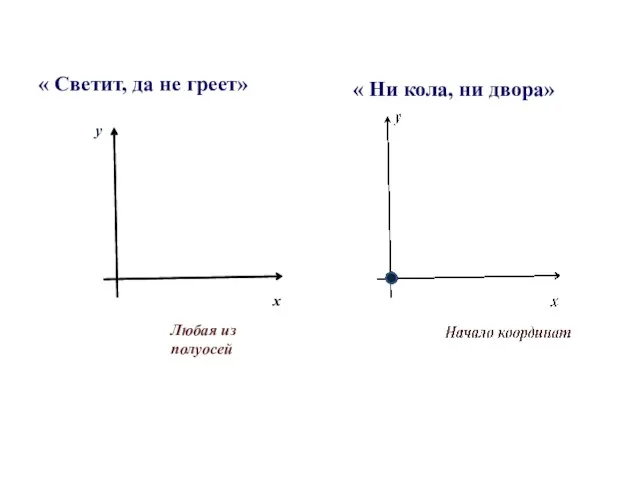
- 29. « Светит, да не греет» « Ни кола, ни двора»
- 30. VI. Подведение итогов 1) Какая функция называется линейной ? 2) Что является графиком линейной функции? 3)
- 31. Домашнее задание: «3» - п.8, №8.6, 8.14 (а, б),8.19(а, б) «4», «5» - п.8, №8.51(а, б),
- 32. VII. Рефлексия - Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно. - Я
- 34. Скачать презентацию







![Выполняем построение графика функции y = -2x + 1, [ -3; 2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/300796/slide-11.jpg)












 экологии
экологии МДОУ детский сад присмотра и оздоровления №7 "Крепыш"
МДОУ детский сад присмотра и оздоровления №7 "Крепыш" Презентация на тему Образ человека в эпоху Ренессанса
Презентация на тему Образ человека в эпоху Ренессанса Конкурентные стратегииприложение к журналу «ЭТАП: Экономическая Теория, Анализ, Практика»
Конкурентные стратегииприложение к журналу «ЭТАП: Экономическая Теория, Анализ, Практика» Topic Famous people
Topic Famous people Прокладка внешнего рейда (карта 38120 2010 года печати)
Прокладка внешнего рейда (карта 38120 2010 года печати) Картинки для обсуждения
Картинки для обсуждения Программа фундаментальных исследований Президиума РАН № 27«ОСНОВЫ ФУНДАМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙНАНОТЕХНОЛОГИЙ И НАНОМАТЕРИАЛО
Программа фундаментальных исследований Президиума РАН № 27«ОСНОВЫ ФУНДАМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙНАНОТЕХНОЛОГИЙ И НАНОМАТЕРИАЛО Тема: «Требования воинской деятельности, предъявляемые к моральным, профессиональным качествам гражданина»
Тема: «Требования воинской деятельности, предъявляемые к моральным, профессиональным качествам гражданина» Железнодорожный транспорт 9 класс
Железнодорожный транспорт 9 класс Создание акустического глубиномера
Создание акустического глубиномера  Экология жилища и здоровье человека
Экология жилища и здоровье человека Интерьер жилого помещения
Интерьер жилого помещения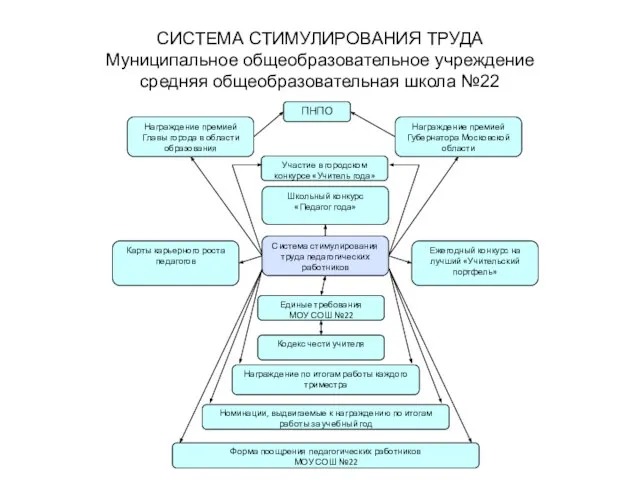 СИСТЕМА СТИМУЛИРОВАНИЯ ТРУДАМуниципальное общеобразовательное учреждение средняя общеобразовательная школа №22
СИСТЕМА СТИМУЛИРОВАНИЯ ТРУДАМуниципальное общеобразовательное учреждение средняя общеобразовательная школа №22 Методика Орловой О.С
Методика Орловой О.С А Н Т И Б И О Т И К И
А Н Т И Б И О Т И К И Геодезические работы при строительстве СПГ Портовая
Геодезические работы при строительстве СПГ Портовая Методы решения неравенств с одной переменной (типовые задания С3) - 1
Методы решения неравенств с одной переменной (типовые задания С3) - 1 Link Pro. Эксклюзивное летнее предложение
Link Pro. Эксклюзивное летнее предложение 10 причин почему ты лучший!
10 причин почему ты лучший! Основные разделы фикха
Основные разделы фикха Изучение графического редактора PAINT
Изучение графического редактора PAINT Водно-электролитные нарушения у хирургических больных, инвазивная терапия
Водно-электролитные нарушения у хирургических больных, инвазивная терапия Праздники в религиях мира
Праздники в религиях мира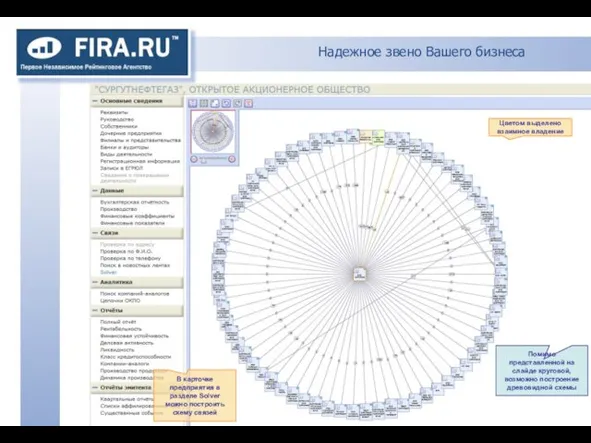 Надежное звено Вашего бизнеса
Надежное звено Вашего бизнеса ГОТОВИМСЯ К ЕГЭ-2010 ПО МАТЕМАТИКЕ
ГОТОВИМСЯ К ЕГЭ-2010 ПО МАТЕМАТИКЕ Филиал ЗАО «Капитал Медицинскоестрахование» в городе Нижнем Новгороде
Филиал ЗАО «Капитал Медицинскоестрахование» в городе Нижнем Новгороде «Интернет: эффективный и экономичный канал привлечения клиентов» Докладчик: руководитель регионального развития сайта IRR.ru Б
«Интернет: эффективный и экономичный канал привлечения клиентов» Докладчик: руководитель регионального развития сайта IRR.ru Б