Содержание
- 2. Содержание 1. Понятие логарифма. 2. Графики логарифмических функций. 3. Свойства логарифмов. 4. Решение логарифмических уравнений. 5.
- 3. Логарифмом положительного числа b по положительному и отличному от 1 основанию а называют показатель степени, в
- 4. В зависимости от значения основания приняты два обозначения Если основанием является 10, то вместо log10 x
- 5. Можно выделить три формулы Из определения логарифма следует следующее тождество: Примеры:
- 6. Графики логарифмических функции 1. y = lg x 2. y = ln x 3. y =
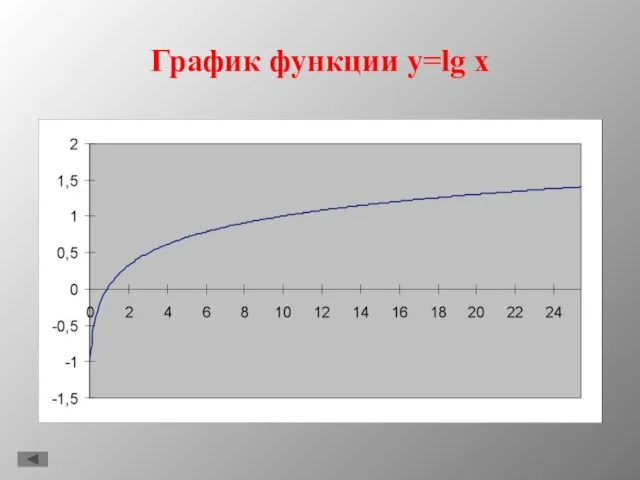
- 7. График функции y=lg x
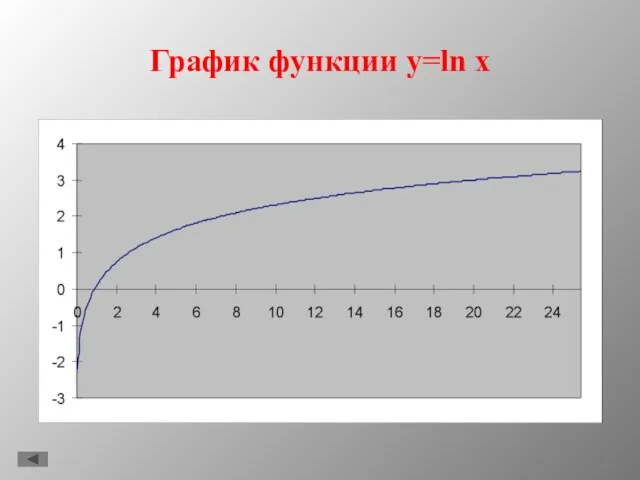
- 8. График функции y=ln x
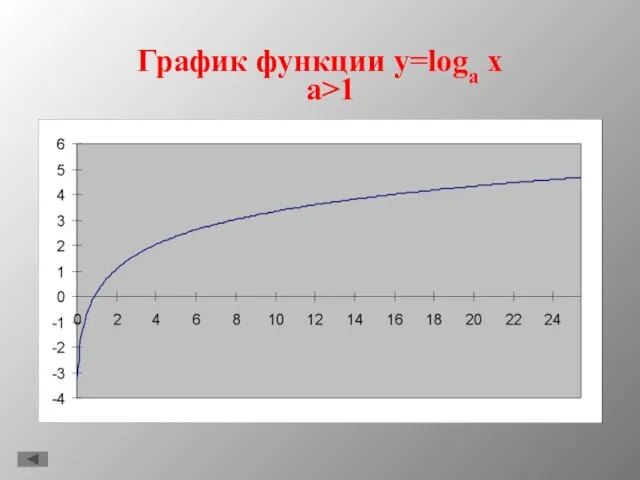
- 9. График функции y=loga x a>1
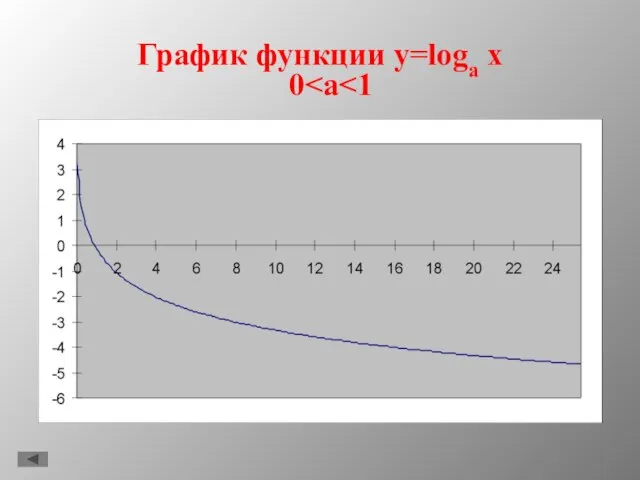
- 10. График функции y=loga x 0
- 11. Свойства f(x)=loga x D(f)=(0;+∞); Не является ни четной, ни нечетной; При a>1 функция возрастающая, при 0
- 12. Свойства логарифмов 1. Логарифм произведения. 2. Логарифм частного. 3. Логарифм степени. 4. Логарифм корня. 5. Переход
- 13. 1. Логарифм произведения равен сумме логарифмов множителей: 2. Логарифм частного равен логарифмов делимого без логарифма делителя:
- 14. 3. Логарифм степени равен произведению показателя степени на логарифм ее основания: 4. Логарифм корня равен отношению
- 15. 5. Переход от одного основания к другому
- 16. Свойства натуральных логарифмов Чтобы по известному десятичному логарифму числа х найти его натуральный логарифм, нужно разделить
- 17. Решения логарифмических уравнений
- 18. Решить уравнение: Значит,
- 19. Решение логарифмических неравенств
- 20. Решите неравенство:
- 22. Скачать презентацию

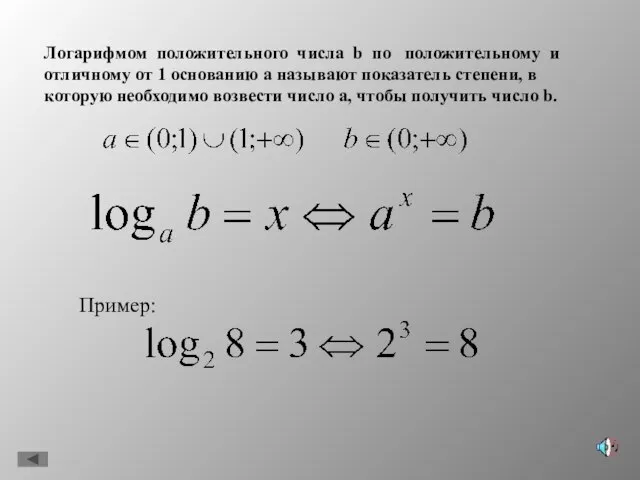





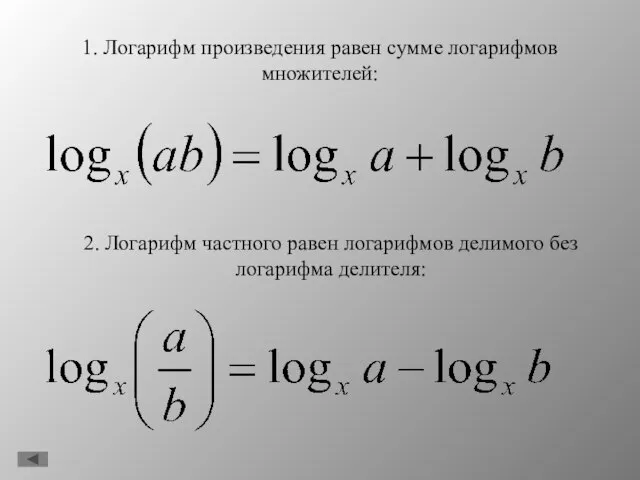







 Права потребителей – знаю, принимаю, действую
Права потребителей – знаю, принимаю, действую Новый вид обуви для лошадей
Новый вид обуви для лошадей Неолит лесной зоны
Неолит лесной зоны  Что приносит занятие наукой?
Что приносит занятие наукой? ОПОРНЫЕ КОНСПЕКТЫ К УЧЕБНИКУ А.В.ПЁРЫШКИНА «ФИЗИКА. 7 КЛАСС»
ОПОРНЫЕ КОНСПЕКТЫ К УЧЕБНИКУ А.В.ПЁРЫШКИНА «ФИЗИКА. 7 КЛАСС» Металисты
Металисты ЭТИ УДИВИТЕЛЬНЫЕ ЖИВОТНЫЕ.
ЭТИ УДИВИТЕЛЬНЫЕ ЖИВОТНЫЕ. Безопасность в интернет
Безопасность в интернет  Анализ, оценка и управление рисками. Приемлемый риск
Анализ, оценка и управление рисками. Приемлемый риск Интерференция света
Интерференция света Мадагаскар
Мадагаскар Национальный орнамент народа коми
Национальный орнамент народа коми Месячник профориентационной работы Дата проведения: март 2009 года
Месячник профориентационной работы Дата проведения: март 2009 года Родственники и прочие реляции (новые задачи с базами данных)
Родственники и прочие реляции (новые задачи с базами данных) Олимпиада 2014 Сочи
Олимпиада 2014 Сочи Программа Театральная педагогика как средство развития универсальных компетенций студентов педагогического вуза
Программа Театральная педагогика как средство развития универсальных компетенций студентов педагогического вуза Стиль милитари в интерьере квартиры
Стиль милитари в интерьере квартиры Отчет о результатах социологического исследования "Киев - районные выборы"
Отчет о результатах социологического исследования "Киев - районные выборы" Барная зона
Барная зона Использование устройств самообслуживания
Использование устройств самообслуживания Грегор Мендель
Грегор Мендель Тема: Энергетический метаболизм микроорганизмов. Методы выделения чистых культур облигатных анаэробов.
Тема: Энергетический метаболизм микроорганизмов. Методы выделения чистых культур облигатных анаэробов. Грамматическая основа предложения
Грамматическая основа предложения Tetra FilterActive 2in1 Новая формула – двойная выгода
Tetra FilterActive 2in1 Новая формула – двойная выгода Использование ИКТ на уроках биологии в целях повышения качества знаний обучающихся
Использование ИКТ на уроках биологии в целях повышения качества знаний обучающихся О применении стандартов НОСТРОЙ в саморегулируемых организациях
О применении стандартов НОСТРОЙ в саморегулируемых организациях ЗНАКОВЫЕ МОДЕЛИ МОДЕЛИРОВАНИЕ И ФОРМАЛИЗАЦИЯ
ЗНАКОВЫЕ МОДЕЛИ МОДЕЛИРОВАНИЕ И ФОРМАЛИЗАЦИЯ Играем в символизм
Играем в символизм