Презентация на тему Метод графов

Введение
Графы заинтересовали нас своей возможностью помогать в решении различных головоломок, математических и логических задач. Так как мы участвуем в математических олимпиадах, то теория графов была особенно актуальна в нашей подготовке. Мы решили разобраться какую роль в обычной жизни играют графы.
содержание

С дворянским титулом «граф» тему нашей работы связывает только общее происхождение от латинского слова «графио» - пишу.
Г
Р
А
Ф
И
О
дальше

История возникновения графов
Термин "граф" впервые появился в книге венгерского математика Д. Кенига в 1936 г., хотя начальные важнейшие теоремы о графах восходят к Л. Эйлеру.
Дальше

Что такое граф
Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. В процессе решения задач математики заметили, что удобно изображать объекты точками, а отношения между ними отрезками или дугами.
Дальше

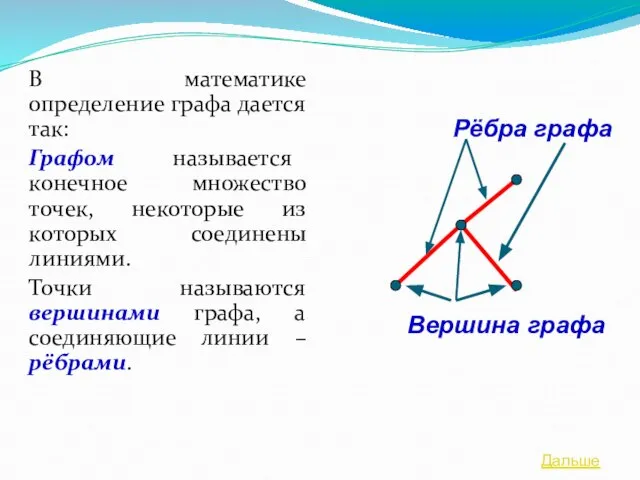
В математике определение графа дается так:
Графом называется конечное множество точек, некоторые из которых соединены линиями.
Точки называются вершинами графа, а соединяющие линии – рёбрами.
Рёбра графа
Вершина графа
Дальше

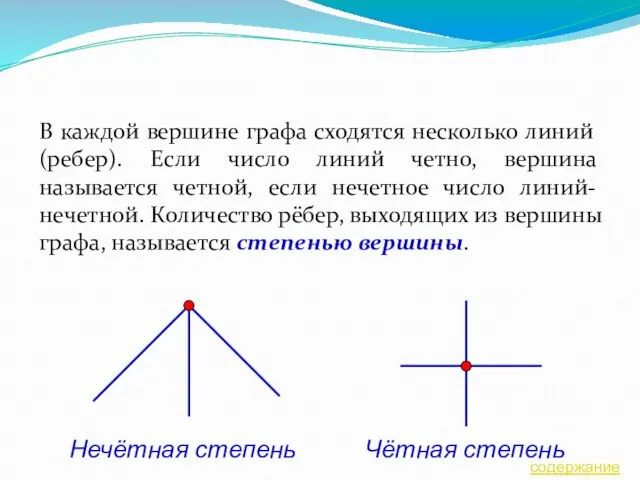
В каждой вершине графа сходятся несколько линий (ребер). Если число линий четно, вершина называется четной, если нечетное число линий- нечетной. Количество рёбер, выходящих из вершины графа, называется степенью вершины.
Нечётная степень
Чётная степень
содержание

Основы теории графов как математической науки заложил в 1736 г. Леонард Эйлер, рассматривая задачу о Кенигсбергских мостах. Сегодня эта задача стала классической.
содержание

Задача о Кенигсбергских мостах
Бывший Кенигсберг (ныне Калининград) стоит на реке Преголь. Некогда там было семь мостов, которые связывали между собой и с берегами два острова. Старые мосты не сохранились, но осталась карта города, где они изображены. Жители города заметили, что они никак не могут совершить прогулку по всем мостам, пройдя по каждому из них ровно один раз.
Дальше

Так возникла задача-головоломка: «можно ли пройти все семь Кенигсбергских мостов ровно один раз и вернуться в исходное место?»
Дальше

дальше
Я здесь уже был!

В 1735 году задача стала известна Леонарду Эйлеру, который выяснил, что пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя. Прохождение по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа.
дальше

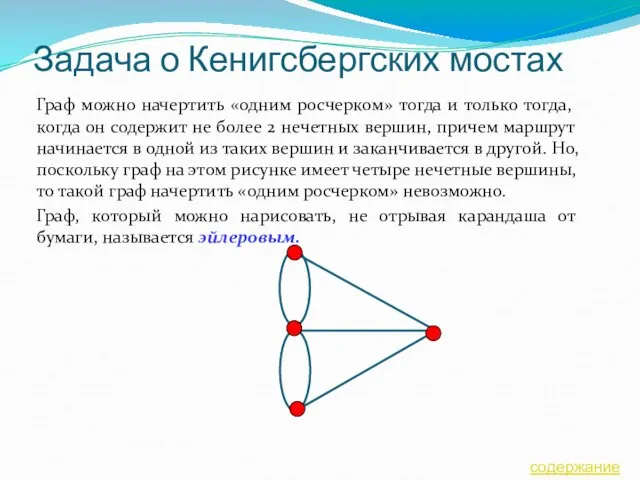
Задача о Кенигсбергских мостах
Граф можно начертить «одним росчерком» тогда и только тогда, когда он содержит не более 2 нечетных вершин, причем маршрут начинается в одной из таких вершин и заканчивается в другой. Но, поскольку граф на этом рисунке имеет четыре нечетные вершины, то такой граф начертить «одним росчерком» невозможно.
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым.
содержание

Одним росчерком
Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.
дальше

Применение графов
С помощью графов упрощается решение математических задач, головоломок, задач на смекалку.
дальше

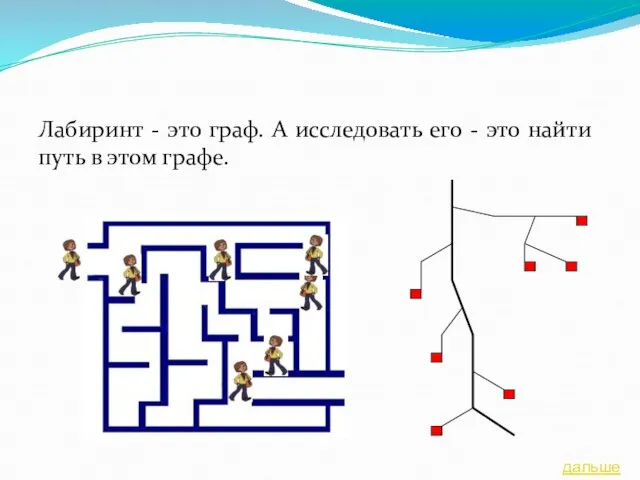
Лабиринт - это граф. А исследовать его - это найти путь в этом графе.
дальше

Использует графы и дворянство.
На рисунке приведена часть генеалогического древа знаменитого дворянского рода Л. Н. Толстого. Здесь его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям.
дальше

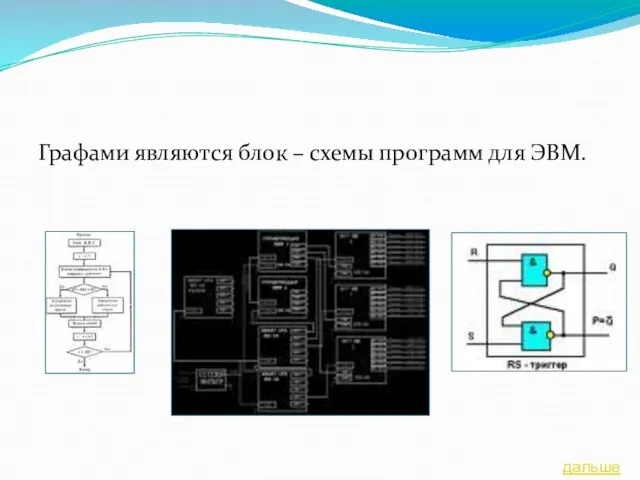
Графами являются блок – схемы программ для ЭВМ.
дальше

Применение графов
Графами являются сетевые графики строительства.
дальше

Типичными графами на географических картах являются изображения железных дорог.
дальше

Применение графов
Типичными графами на картах города являются схемы движения городского транспорта.
дальше

Применение графов
Типичными графами являются схемы авиалиний, которые часто вывешиваются в аэропортах.
дальше

Применение графов
Графом является и система улиц города. Его вершины – площади и перекрестки, а ребра – улицы.
дальше

Применение графов
Графы есть и на картах звездного неба.
дальше

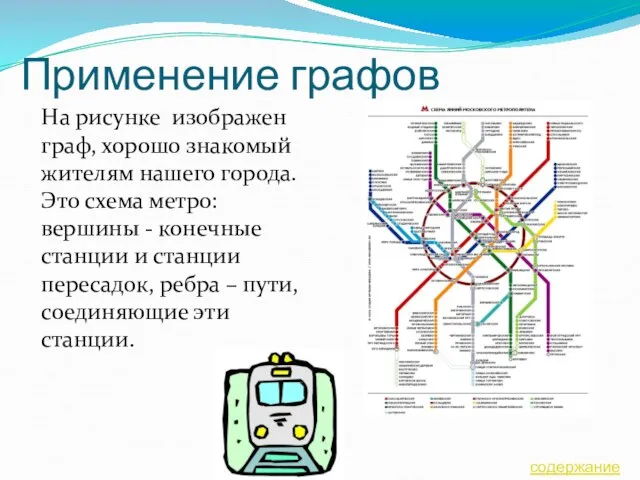
Применение графов
На рисунке изображен граф, хорошо знакомый жителям нашего города. Это схема метро: вершины - конечные станции и станции пересадок, ребра – пути, соединяющие эти станции.
содержание

Решите задачи

Нарисуйте граф,
состоящий из четырех одноклассников:
Саша и Маша
Саша и Даша
Маша и Гриша
Гриша и Саша

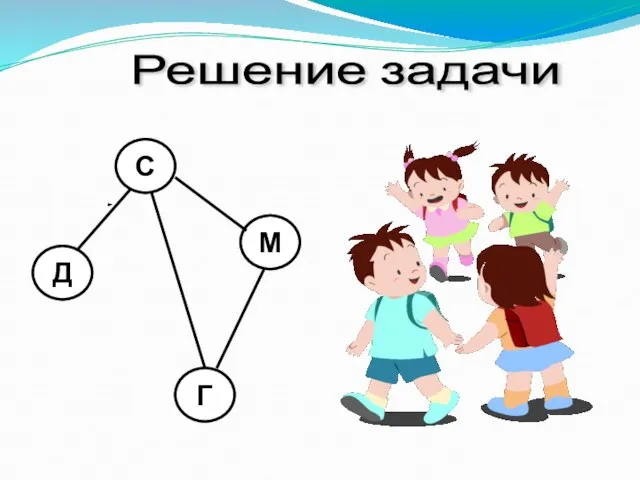
Решение задачи

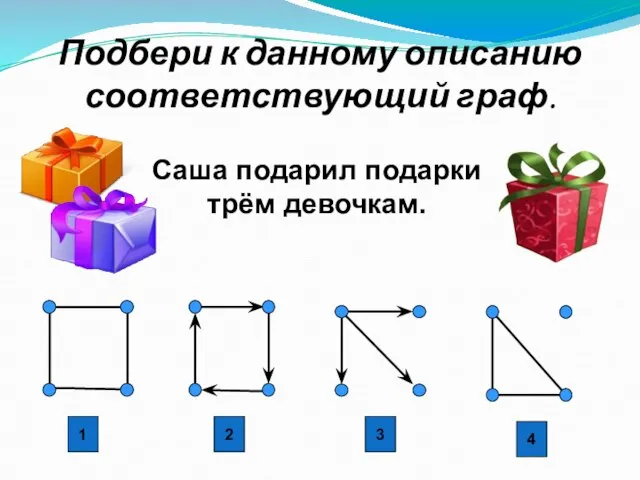
Подбери к данному описанию соответствующий граф.
Саша подарил подарки трём девочкам.
1
2
3
4

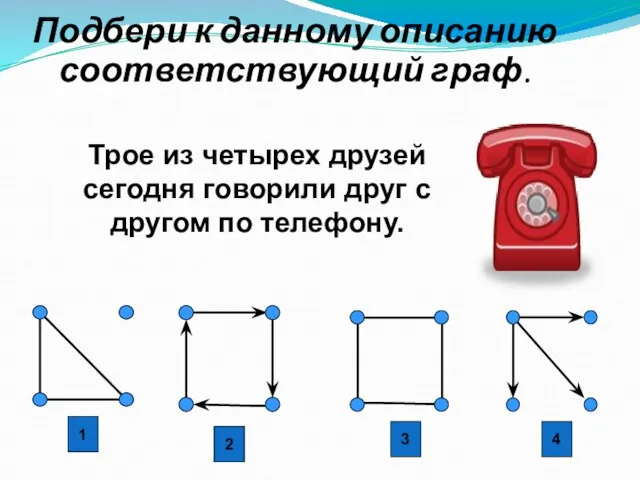
Трое из четырех друзей сегодня говорили друг с другом по телефону.
Подбери к данному описанию
соответствующий граф.
2
3
4
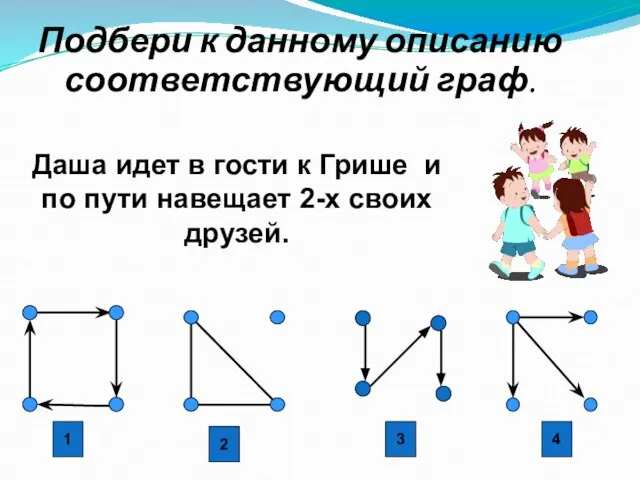
1

Даша идет в гости к Грише и по пути навещает 2-х своих друзей.
Подбери к данному описанию
соответствующий граф.
1
2
3
4

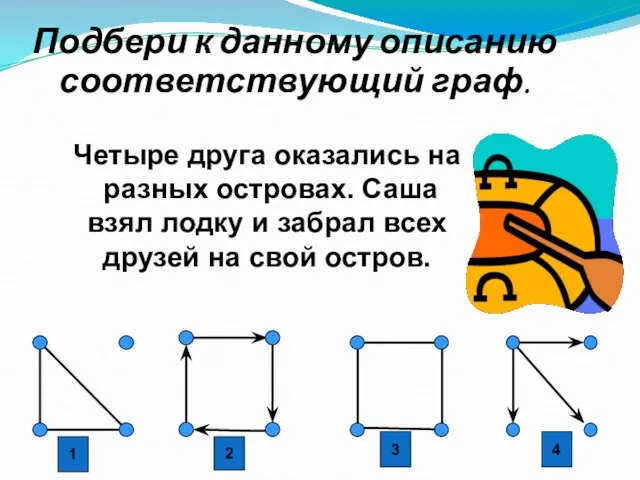
Подбери к данному описанию
соответствующий граф.
Четыре друга оказались на
разных островах. Саша
взял лодку и забрал всех
друзей на свой остров.
2
3
4
1

Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Венера; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?

Решение
Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Теперь сразу видно, что долететь с Земли до Марса нельзя.

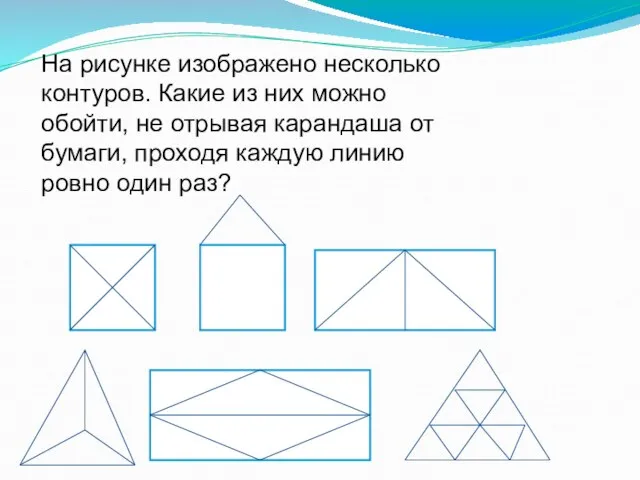
На рисунке изображено несколько контуров. Какие из них можно обойти, не отрывая карандаша от бумаги, проходя каждую линию ровно один раз?