Презентация на тему Параллелаграмм

Цели:
30.11.2012
Ввести понятие параллелограмма.
Рассмотреть свойства параллелограмма.
Рассмотреть признаки параллелограмма.
Решение базовых задач.
www.konspekturoka.ru

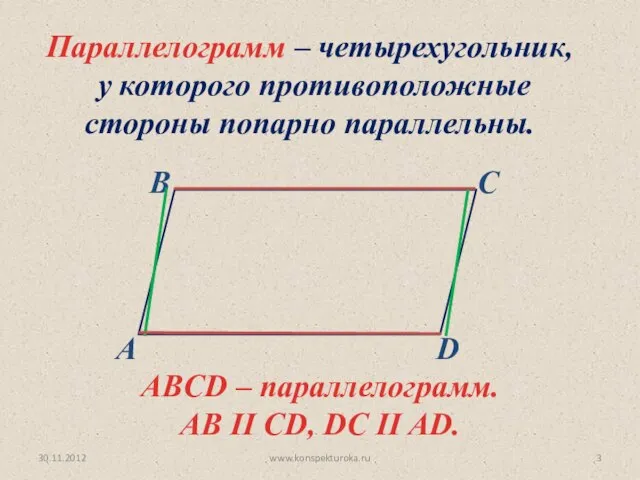
30.11.2012
www.konspekturoka.ru
ABCD – параллелограмм.
AB II CD, DC II AD.
Параллелограмм – четырехугольник,
у которого противоположные стороны попарно параллельны.

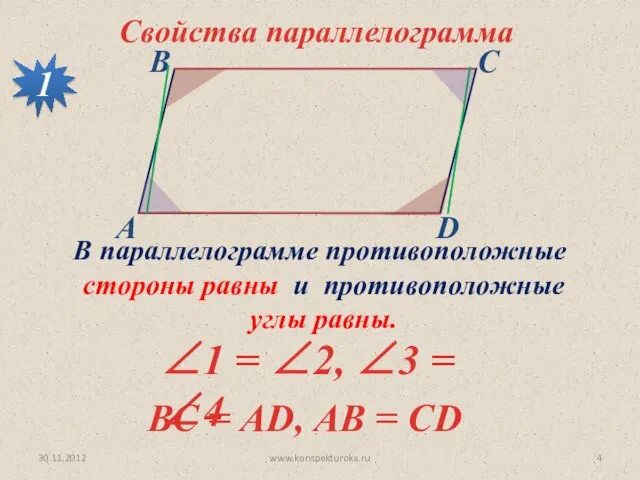
30.11.2012
www.konspekturoka.ru
Свойства параллелограмма
1
В параллелограмме противоположные
стороны равны и противоположные
углы равны.
∠1 = ∠2, ∠3 = ∠4
ВС = AD, АВ = СD

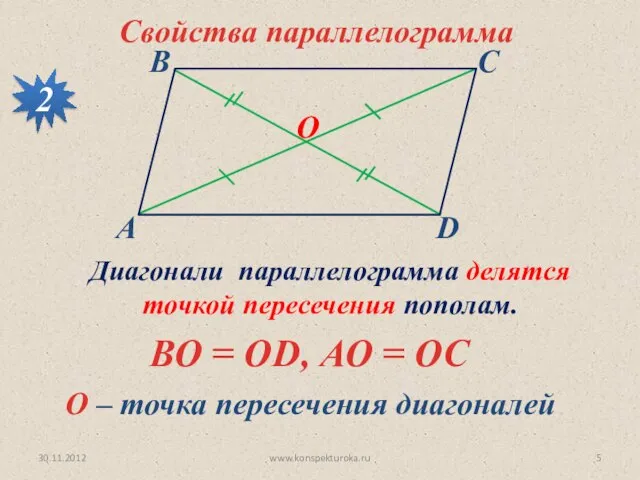
30.11.2012
www.konspekturoka.ru
Свойства параллелограмма
2
Диагонали параллелограмма делятся точкой пересечения пополам.
О
ВО = ОD, АО = ОС
О – точка пересечения диагоналей

30.11.2012
www.konspekturoka.ru
Свойства параллелограмма
3
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°.
∠А + ∠D = 180° ,
∠D + ∠C = 180° ,
∠А + ∠B = 180° ,
∠В + ∠C = 180° ,

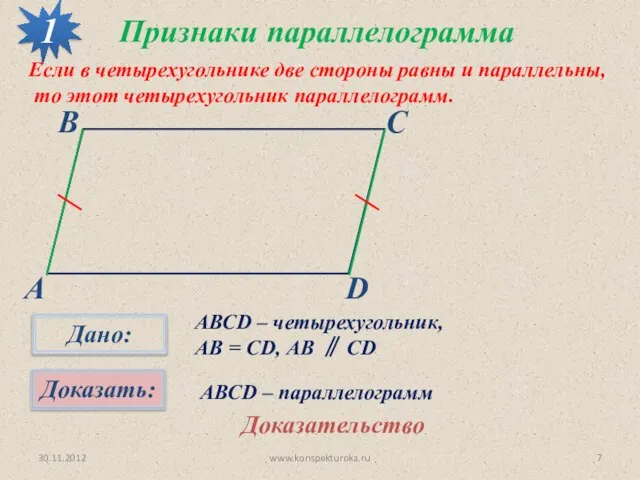
30.11.2012
www.konspekturoka.ru
Признаки параллелограмма
1
Если в четырехугольнике две стороны равны и параллельны,
то этот четырехугольник параллелограмм.
АВСD – четырехугольник,
АВ = CD, АВ ∥ CD
АВСD – параллелограмм
Доказательство

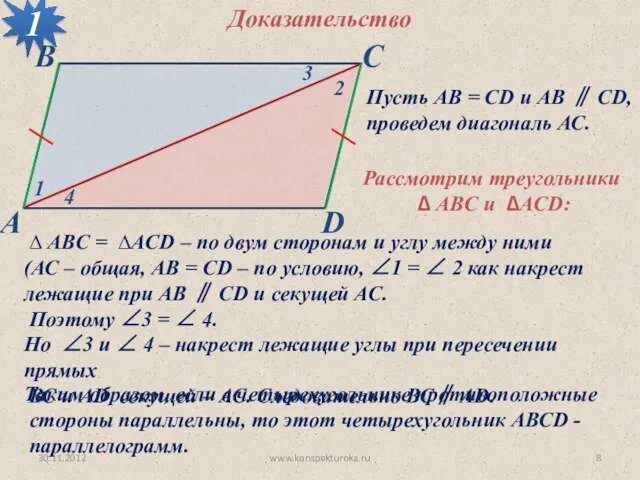
30.11.2012
www.konspekturoka.ru
1
Доказательство
Пусть АВ = СD и АВ ∥ СD,
проведем диагональ АС.
Рассмотрим треугольники ∆ АBC и ∆ACD:
∆ АBC = ∆ACD – по двум сторонам и углу между ними
(АС – общая, АВ = СD – по условию, ∠1 = ∠ 2 как накрест лежащие при АВ ∥ СD и секущей АС.
Поэтому ∠3 = ∠ 4.
1
2
3
4
Но ∠3 и ∠ 4 – накрест лежащие углы при пересечении прямых
ВС и AD секущей – АС. Следовательно ВС∥ AD.
Таким образом, если в четырехугольнике противоположные
стороны параллельны, то этот четырехугольник АВСD -
параллелограмм.

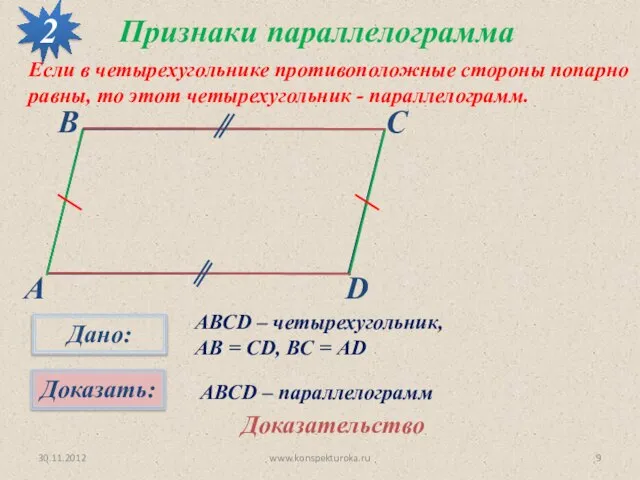
30.11.2012
www.konspekturoka.ru
Признаки параллелограмма
2
Если в четырехугольнике противоположные стороны попарно
равны, то этот четырехугольник - параллелограмм.
АВСD – четырехугольник,
АВ = CD, ВС = АD
АВСD – параллелограмм
Доказательство

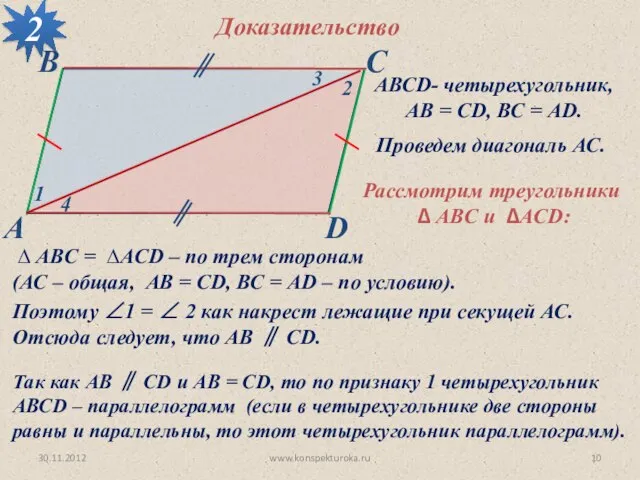
30.11.2012
www.konspekturoka.ru
2
АВСD- четырехугольник,
АВ = CD, ВС = АD.
Доказательство
Рассмотрим треугольники
∆ АBC и ∆ACD:
∆ АBC = ∆ACD – по трем сторонам
(АС – общая, АВ = СD, ВС = АD – по условию).
Поэтому ∠1 = ∠ 2 как накрест лежащие при секущей АС.
Отсюда следует, что АВ ∥ СD.
Проведем диагональ АС.
Так как АВ ∥ СD и АВ = СD, то по признаку 1 четырехугольник АВСD – параллелограмм (если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм).

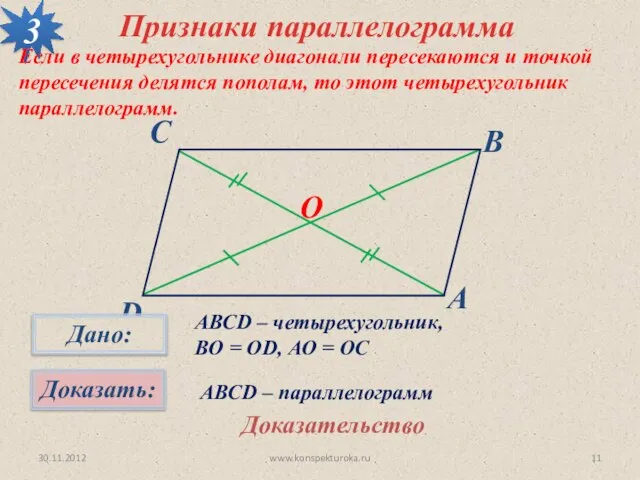
30.11.2012
www.konspekturoka.ru
3
О
Признаки параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм.
АВСD – четырехугольник,
ВО = ОD, АО = ОС
АВСD – параллелограмм
Доказательство

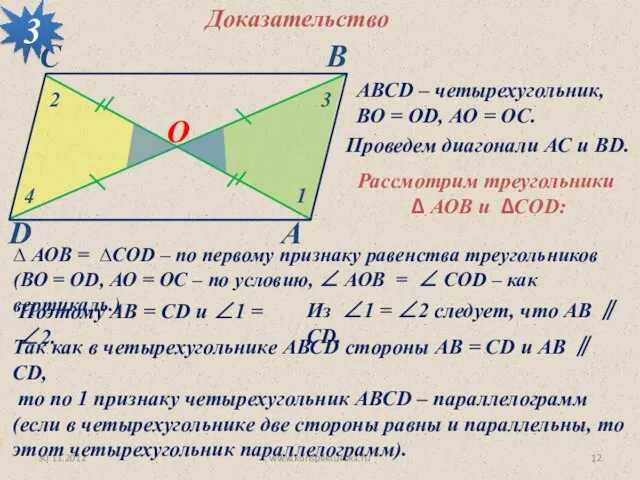
30.11.2012
www.konspekturoka.ru
3
О
АВСD – четырехугольник,
ВО = ОD, АО = ОС.
Доказательство
Проведем диагонали АС и BD.
Рассмотрим треугольники
∆ АОB и ∆CОD:
∆ АОB = ∆CОD – по первому признаку равенства треугольников
(ВО = ОD, АО = ОС – по условию, ∠ АОB = ∠ CОD – как вертикаль.)
Поэтому АВ = CD и ∠1 = ∠2.
Из ∠1 = ∠2 следует, что АВ ∥ CD.
Так как в четырехугольнике АВСD стороны АВ = CD и АВ ∥ CD,
то по 1 признаку четырехугольник АВСD – параллелограмм (если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм).

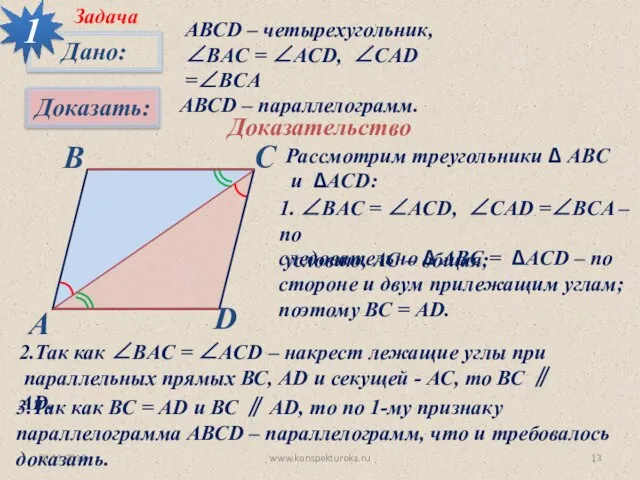
30.11.2012
www.konspekturoka.ru
1
АВСD – четырехугольник,
∠BАC = ∠ACD, ∠CAD =∠BCA
АВСD – параллелограмм.
Доказательство
Рассмотрим треугольники ∆ АBC
и ∆ACD:
1. ∠BАC = ∠ACD, ∠CAD =∠BCA – по
условию, АС – общая;
следовательно ∆ АBC = ∆ACD – по
стороне и двум прилежащим углам;
поэтому ВС = AD.
2.Так как ∠BАC = ∠ACD – накрест лежащие углы при
параллельных прямых ВС, AD и секущей - АС, то ВС ∥ AD.
3.Так как ВС = AD и ВС ∥ AD, то по 1-му признаку параллелограмма АВСD – параллелограмм, что и требовалось доказать.
Задача