Содержание
- 2. Содержание Историческая справка Призма и ее свойства Решение задач Задачи для самостоятельной работы Литература
- 3. Еще в древности существовали два пути определения геометрических понятий. Первый вел от фигур высшего порядка к
- 4. Второй путь ведет, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично
- 5. В появившихся позже на протяжении веков учебниках геометрии принималась за основу то одна, то другая, а
- 6. Евклид употребляет термин «плоскость» как в широком смысле (Рассматривая ее неограниченно продолженной во все направления), так
- 7. В XVIII в. Тейлор дал такое определение призмы: это многогранник, у которого все грани, кроме двух,
- 8. В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и
- 9. Термин “призма” греческого происхождения и буквально означает “отпиленное” ПризмА
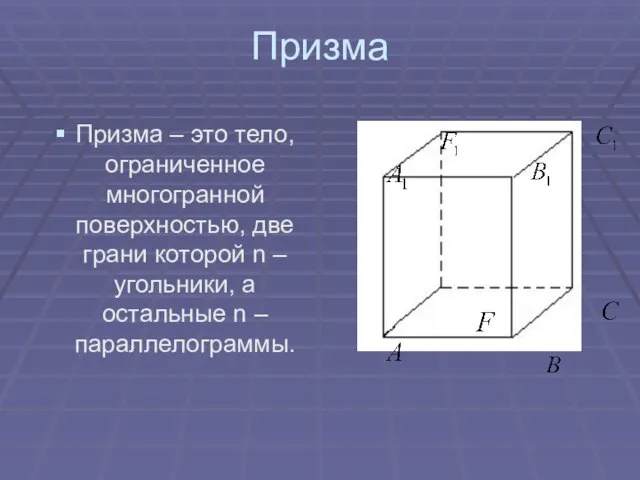
- 10. Призма Призма – это тело, ограниченное многогранной поверхностью, две грани которой n – угольники, а остальные
- 11. β Рассмотрим два равных многоугольника и , расположенных в параллельных плоскостях и так, что отрезки ,
- 12. Каждый из n четырехугольников является параллелограммов, так как имеет попарно параллельные противоположные стороны. Например, в четырехугольнике
- 13. ( рис. 3) Многоугольники и называются основаниями, а параллелограммы – боковыми гранями. Отрезки , называются боковыми
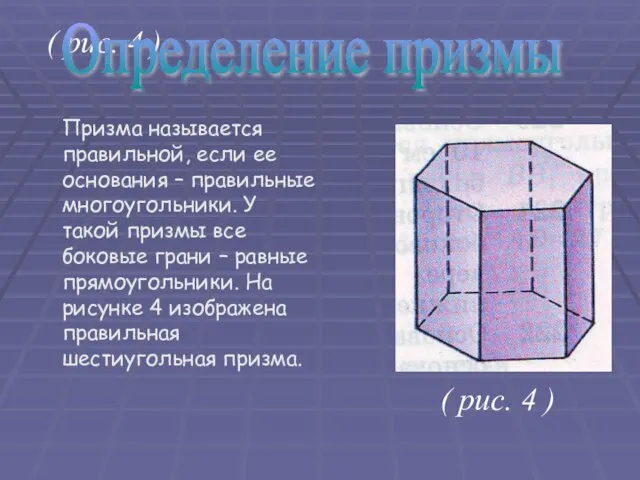
- 14. ( рис. 4 ) Призма называется правильной, если ее основания – правильные многоугольники. У такой призмы
- 15. Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы
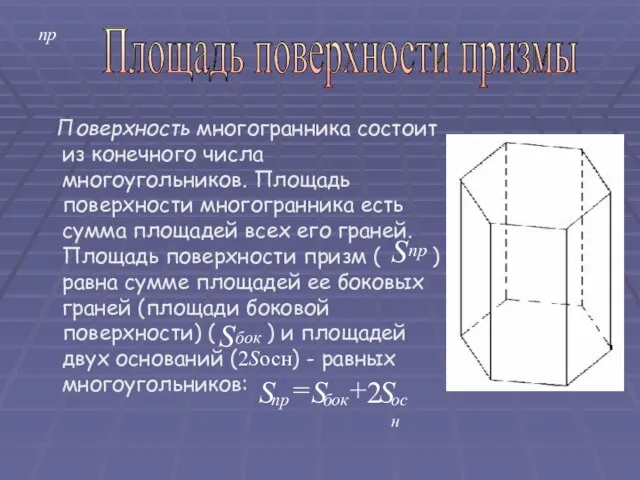
- 16. пр Поверхность многогранника состоит из конечного числа многоугольников. Площадь поверхности многогранника есть сумма площадей всех его
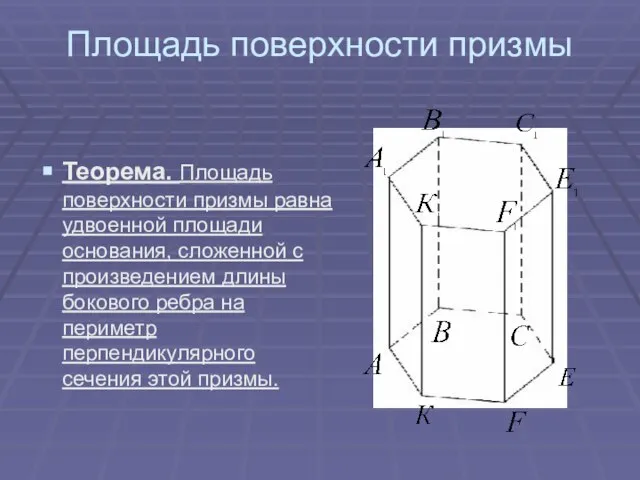
- 17. Площадь поверхности призмы Теорема. Площадь поверхности призмы равна удвоенной площади основания, сложенной с произведением длины бокового
- 18. Боковые грани прямой призмы – прямоугольники, основания которых – стороны призмы, а высоты равны высоте h
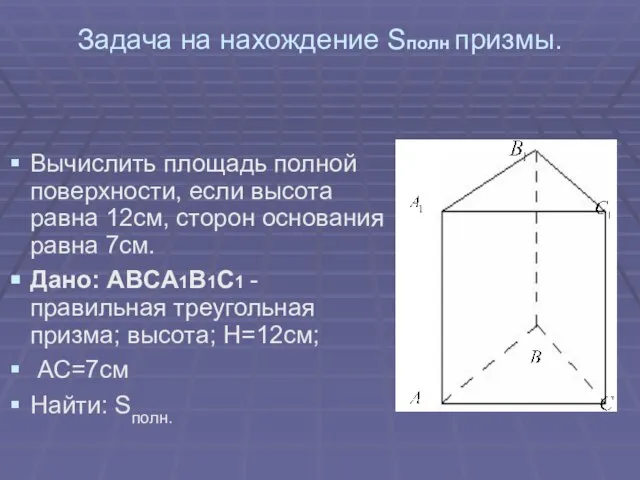
- 19. Задача на нахождение Sполн призмы. Вычислить площадь полной поверхности, если высота равна 12см, сторон основания равна
- 20. Решение: Ответ:
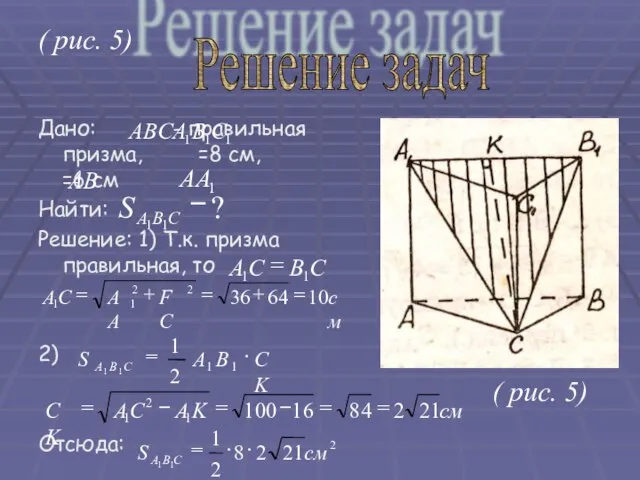
- 21. ( рис. 5) Дано: - правильная призма, =8 см, =6 см Найти: Решение: 1) Т.к. призма
- 22. Дано: - правильный Доказать: а) б) прямоугольник Доказательство: 1) Т.к. , то АН - биссектриса -
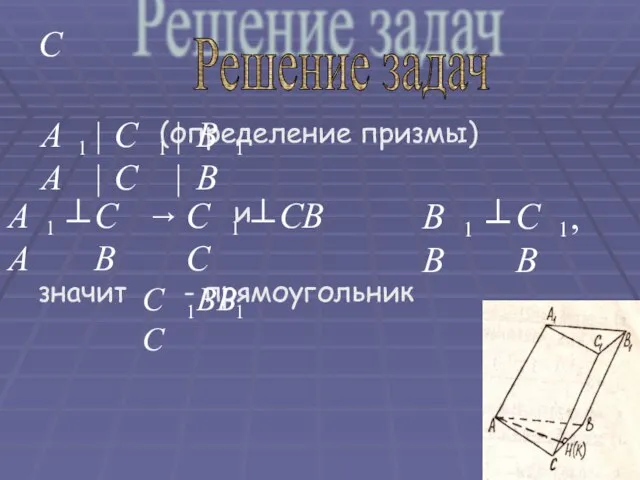
- 23. (определение призмы) и значит - прямоугольник C Решение задач
- 24. Докажите, что: а) у прямой призмы все боковые грани – прямоугольники; б) у правильной призмы все
- 25. Основаниями прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8
- 27. Скачать презентацию

















 Отдельные виды договорных отношений в жилищном праве
Отдельные виды договорных отношений в жилищном праве Организация велостоянки для гимназии №1
Организация велостоянки для гимназии №1 О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го
О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го Урок русского языка в 6 классе по теме: «Правописание сложных существительных»
Урок русского языка в 6 классе по теме: «Правописание сложных существительных» Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании
Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании Невидимые нити в весеннем лесу (2 класс)
Невидимые нити в весеннем лесу (2 класс) Игрушки из носочков своими руками №7
Игрушки из носочков своими руками №7 Введение в специальность
Введение в специальность Герцог Ами
Герцог Ами Трение. Вредно или полезно
Трение. Вредно или полезно Правовой статус личности. Гражданство РФ
Правовой статус личности. Гражданство РФ Социальная психология
Социальная психология Презентация на тему АФАНАСИЙ НИКИТИН
Презентация на тему АФАНАСИЙ НИКИТИН  Теория обучения
Теория обучения Презентация на тему Our Environment (Наша окружающая среда)
Презентация на тему Our Environment (Наша окружающая среда) Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС)
Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС) Презентация по информатике на тему: «Устройства вывода информации, монитор.»
Презентация по информатике на тему: «Устройства вывода информации, монитор.» Круглопольское сельское поселение
Круглопольское сельское поселение Прайс косметологических услуг салона Забота о вас
Прайс косметологических услуг салона Забота о вас Патрон грязеуловителя
Патрон грязеуловителя Назначение изделия и его описание
Назначение изделия и его описание Планирование и организация процесса закупок материальных ресурсов промышленного предприятия
Планирование и организация процесса закупок материальных ресурсов промышленного предприятия Распространение объектно-ориентированного подхода на информационную безопасность
Распространение объектно-ориентированного подхода на информационную безопасность Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк.
Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк. Пейзаж в графике
Пейзаж в графике Рогожка. Коллекция однотонных штор
Рогожка. Коллекция однотонных штор _Презентация. Предоставление
_Презентация. Предоставление Презентация
Презентация