Содержание
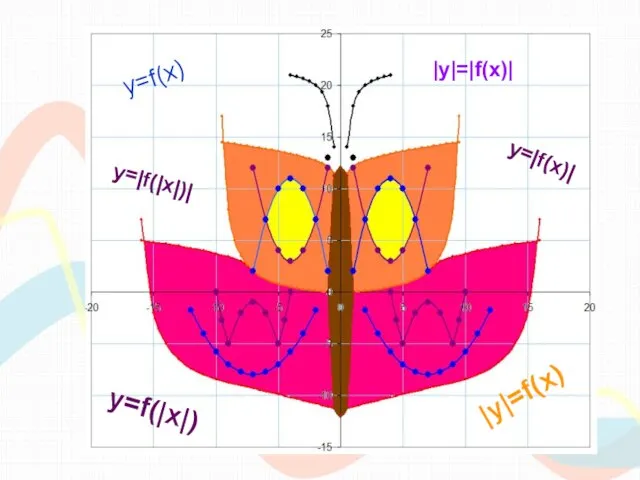
- 2. y=f(x) y=|f(x)| y=f(|x|) |y|=f(x) |y|=|f(x)| y=|f(|x|)|
- 3. Актуальность: Эта тема актуальна, т.к. в конце 11 класса необходимо сдавать единый государственный экзамен по математике,
- 4. Цель: Изучение способов построения графиков функций с помощью различных преобразований. Задачи: Исследовать взаимосвязь графика функции y=f(x)
- 5. Рабочая гипотеза: графики сложных функций, можно построить с помощью преобразований графика исходной функции. Объект – графики
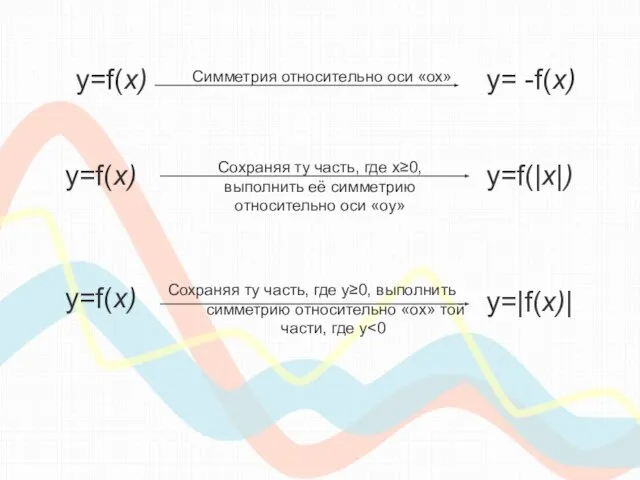
- 6. y=f(х) y= -f(х) Симметрия относительно оси «ох» y=f(х) y=f(|х|) Сохраняя ту часть, где х≥0, выполнить её
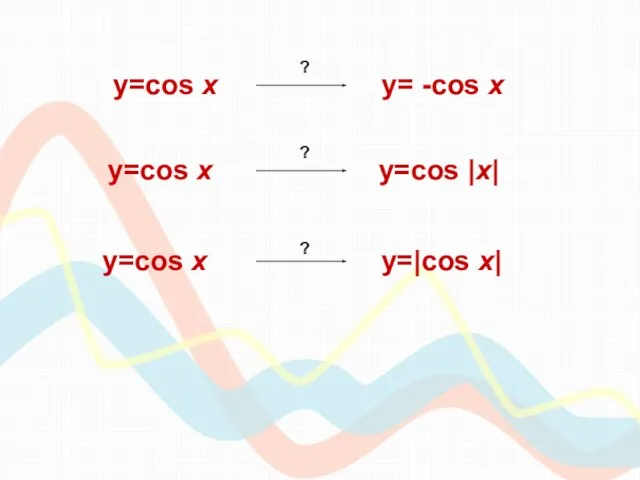
- 7. y=cos х y=cos |x| y=cos х y= -cos x y=cos х y=|cos x| ? ? ?
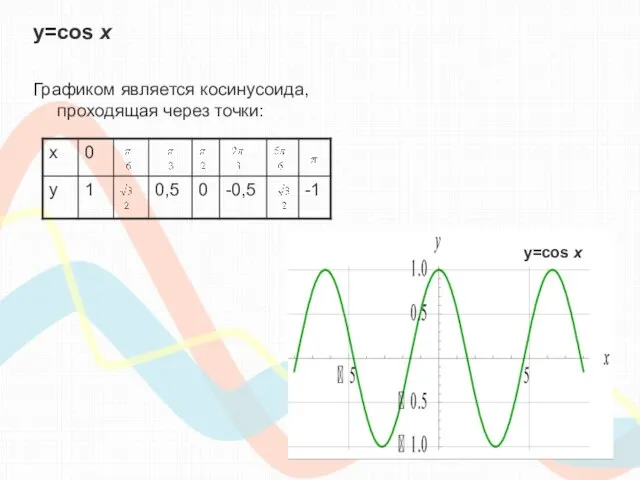
- 8. y=cos х Графиком является косинусоида, проходящая через точки: y=cos х
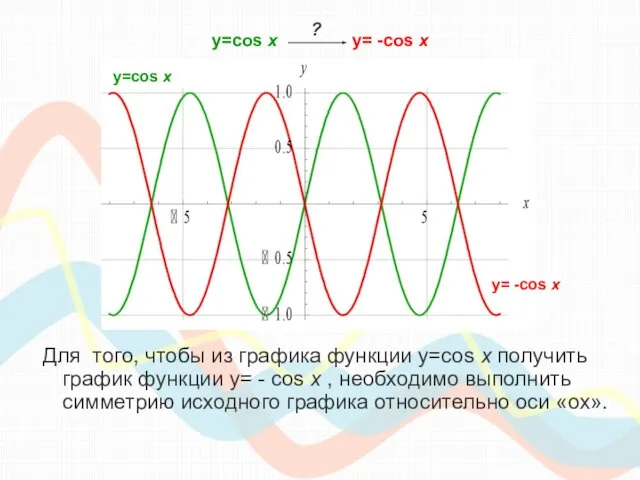
- 9. y=cos х y= -cos x Для того, чтобы из графика функции y=cos x получить график функции
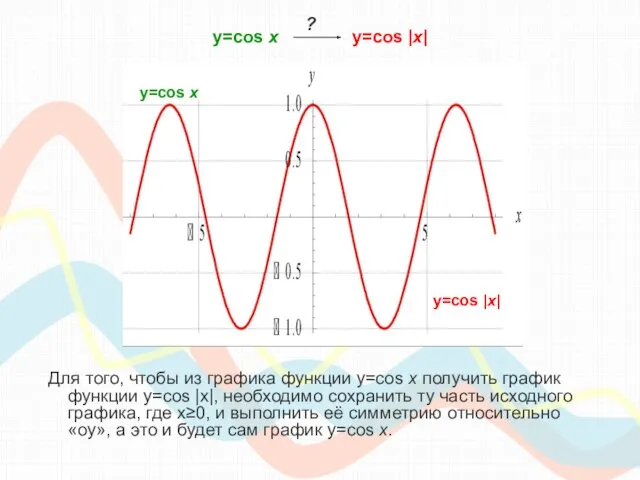
- 10. y=cos х y=cos |x| Для того, чтобы из графика функции y=cos x получить график функции y=cos
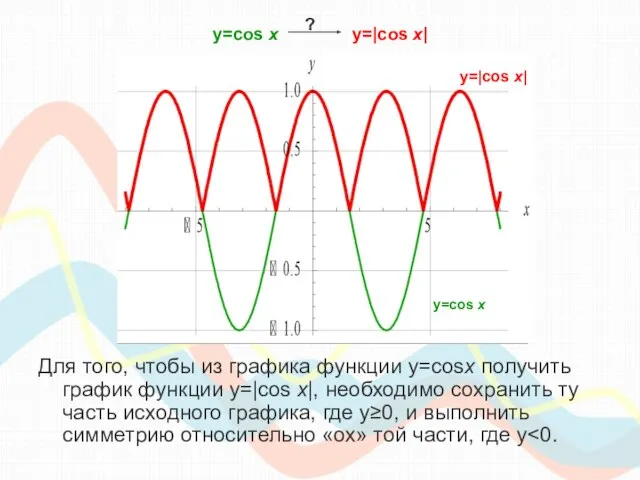
- 11. y=cos х y=|cos x| Для того, чтобы из графика функции y=cosx получить график функции y=|cos x|,
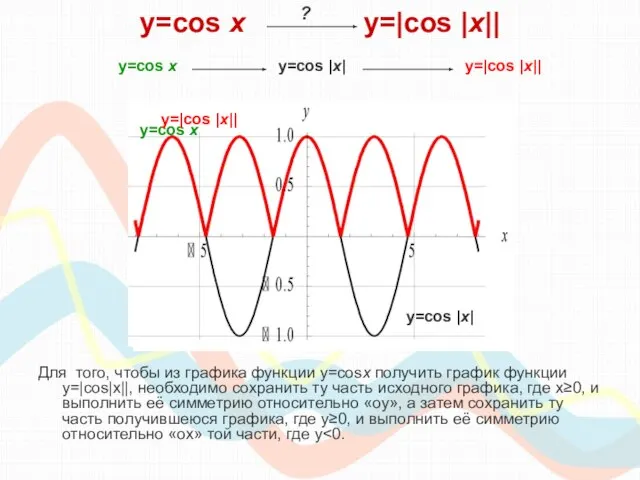
- 12. y=cos х y=|cos |x|| Для того, чтобы из графика функции y=cosx получить график функции y=|cos|x||, необходимо
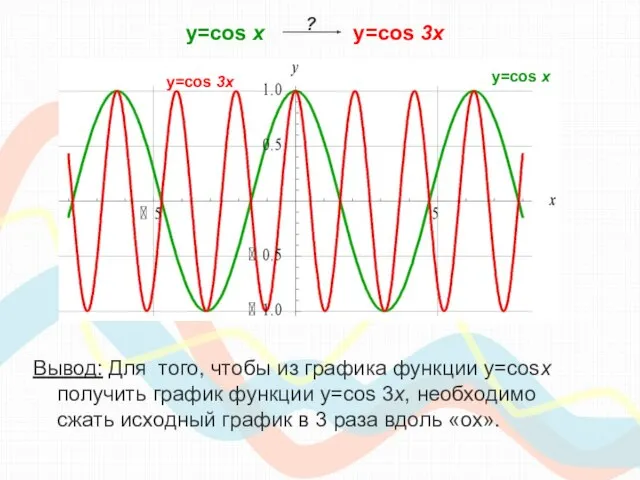
- 13. y=cos х y=cos 3x y=cos 3x График этой функции проходит через точки: ?
- 14. y=cos х y=cos 3x Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos
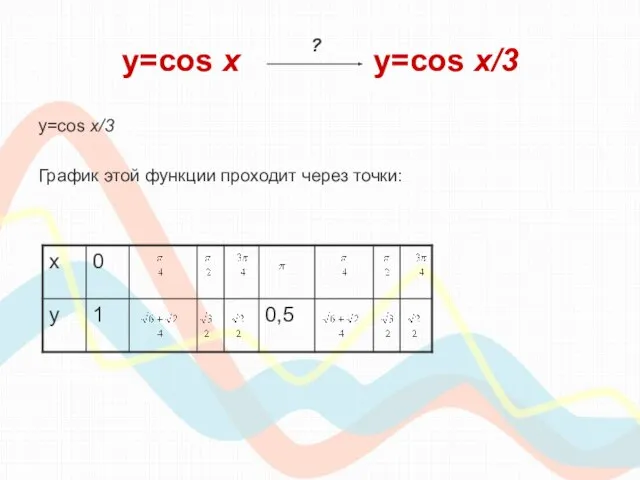
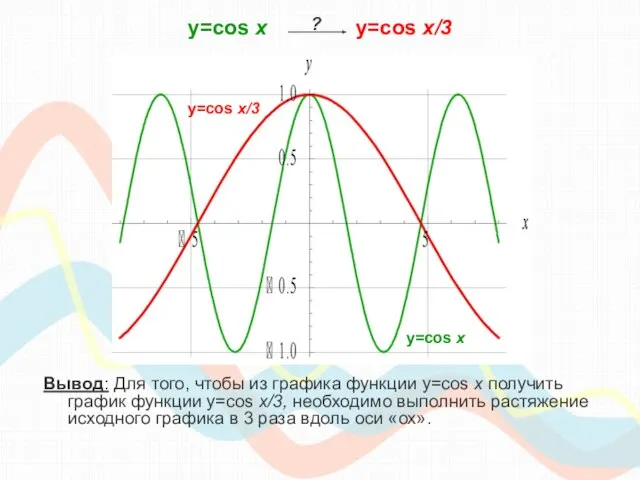
- 15. y=cos х y=cos x/3 y=cos x/3 График этой функции проходит через точки: ?
- 16. y=cos х y=cos x/3 Вывод: Для того, чтобы из графика функции y=cos x получить график функции
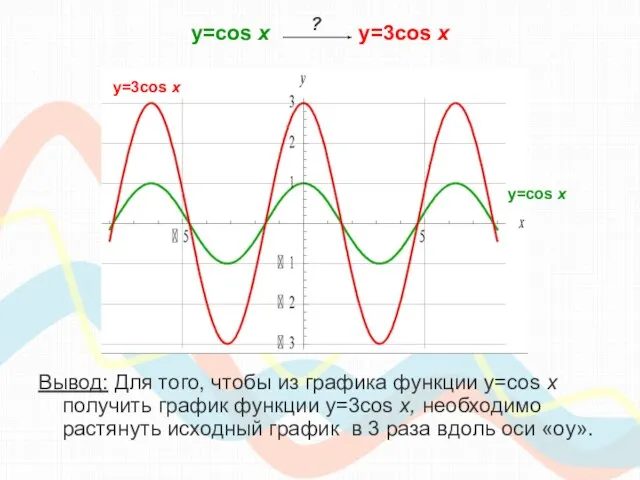
- 17. y=cos х y=3cos x y=3cos x График проходит через точки: ?
- 18. y=cos х y=3cos x Вывод: Для того, чтобы из графика функции y=cos x получить график функции
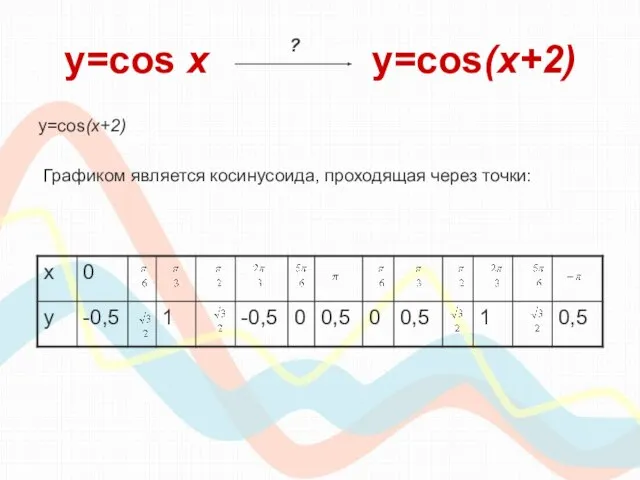
- 19. y=cos х y=cos(x+2) y=cos(x+2) Графиком является косинусоида, проходящая через точки: ?
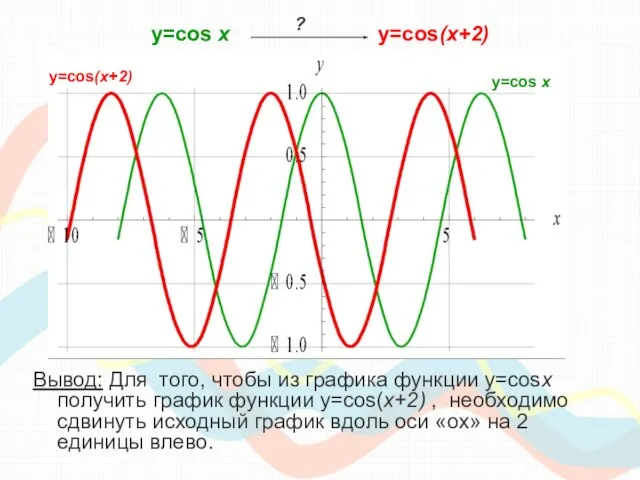
- 20. y=cos х y=cos(x+2) Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos(x+2) ,
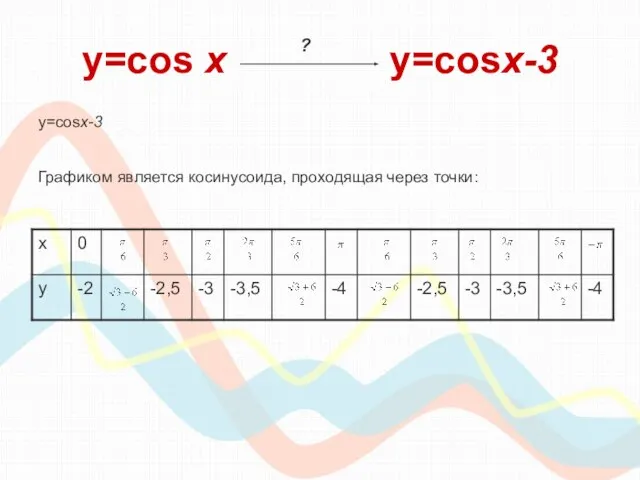
- 21. y=cos х y=cosx-3 y=cosx-3 Графиком является косинусоида, проходящая через точки: ?
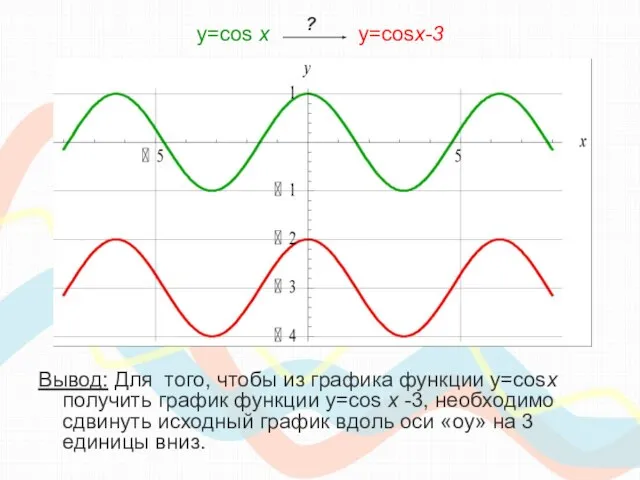
- 22. y=cos х y=cosx-3 Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos x
- 23. Итог: y=f(x) y=f(|x|) Сохраняя ту часть исходного графика, где х≥0, выполнить её симметрию относительно оси «оу»
- 24. Мы знаем, что для того, чтобы из графика функции получить график функции необходимо растянуть исходный график
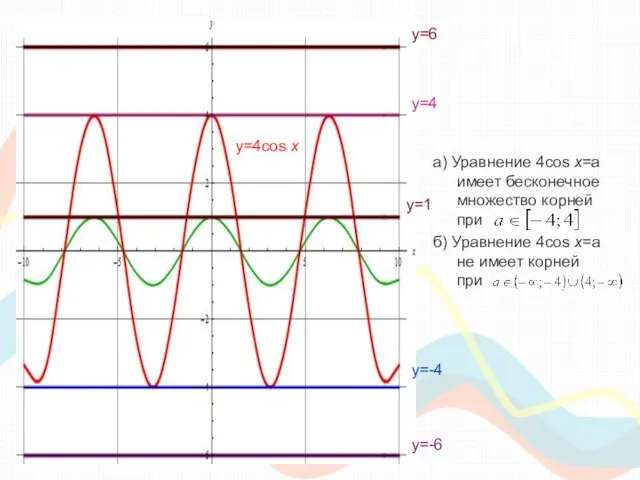
- 25. а) Уравнение 4cos x=a имеет бесконечное множество корней при б) Уравнение 4cos x=a не имеет корней
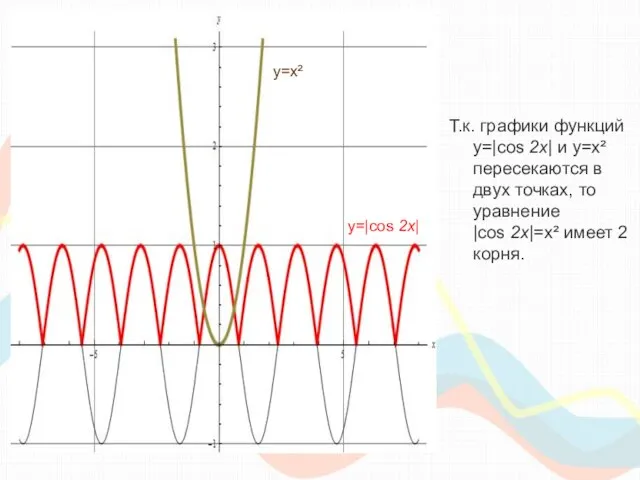
- 26. Исследование количества корней уравнения: |cos 2x|=x² y=|cos 2x| y=cos x y=cos 2x y=|cos 2x| Мы знаем,
- 27. Т.к. графики функций y=|cos 2x| и y=x² пересекаются в двух точках, то уравнение |cos 2x|=x² имеет
- 28. Функции, использованные для построения рисунка
- 33. Заключение Цель достигнута, мы изучили способы построения графиков функций с помощью различных преобразований. Задачи выполнены, мы
- 34. Значимость полученных результатов: сейчас нам стало известно, как строить графики сложных функций с помощью преобразований графика
- 36. Скачать презентацию












 Трудности в обучении письму и чтению по системе Брайля
Трудности в обучении письму и чтению по системе Брайля Вкусный крафт. The Bar Botanist
Вкусный крафт. The Bar Botanist Презентация на тему Анализ деятельности коммерческого банка
Презентация на тему Анализ деятельности коммерческого банка Гуманитарный факультет Горловского института иностранных языков
Гуманитарный факультет Горловского института иностранных языков Перспективы развития системы доменных имен. Взгляд из России
Перспективы развития системы доменных имен. Взгляд из России Евгений Чарушин
Евгений Чарушин Презентация на тему Колебательный контур. Свободные и вынужденные колебания резонанс
Презентация на тему Колебательный контур. Свободные и вынужденные колебания резонанс
 Магия вкуса
Магия вкуса Презентация на тему Храмы Древней Греции
Презентация на тему Храмы Древней Греции  Мой словарик
Мой словарик Как быть эффективным волонтером
Как быть эффективным волонтером Презентация на тему Взаимные превращения жидкости, пара и твёрдого тела
Презентация на тему Взаимные превращения жидкости, пара и твёрдого тела ИСКУСТВЕННОЕ И СМЕШАННОЕ ВСКАРМЛИВАНИЕ
ИСКУСТВЕННОЕ И СМЕШАННОЕ ВСКАРМЛИВАНИЕ Технологии развивающего обучения
Технологии развивающего обучения Как уберечь ребенка от насилия?
Как уберечь ребенка от насилия? Apple Day
Apple Day Презентация на тему Звонкий согласный [з] [з']. Буква З з
Презентация на тему Звонкий согласный [з] [з']. Буква З з  Тищенко Ольга Ивановна
Тищенко Ольга Ивановна Презентация на тему Ветер
Презентация на тему Ветер Современный выпускник глазами учителей, родителей, учащихся. Модель выпускника
Современный выпускник глазами учителей, родителей, учащихся. Модель выпускника Христианская этика
Христианская этика Поиск данных.Условия поиска.
Поиск данных.Условия поиска. Папка личных достижениий («Портфолио»)выпускника основной школы
Папка личных достижениий («Портфолио»)выпускника основной школы Технология формирования слоистых структур феррит-сегнетоэлектрик
Технология формирования слоистых структур феррит-сегнетоэлектрик Этическая основа культуры
Этическая основа культуры Основные сведения о силовых электронных приборах. Лекция № 1
Основные сведения о силовых электронных приборах. Лекция № 1 ТРОПИНКА, ВЕДУЩАЯ К БЕЗДНЕ…
ТРОПИНКА, ВЕДУЩАЯ К БЕЗДНЕ… Сфера производства
Сфера производства